格路计数和反射容斥
如何将这个 dp 式子优化到线性:
1 基本内容
考虑一个二维平面上,只能向右边或者上面走。也就是,当你走到 \((x,y)\) 的时候,你可以走到 \((x + 1, y)\) 或者 \((x, y + 1)\)。
容易发现,走到 \((n, m)\) 的方案数为 \(\dbinom{n + m}{n}\)。
如果有一条线 \(y = x + b\) 不可碰撞:
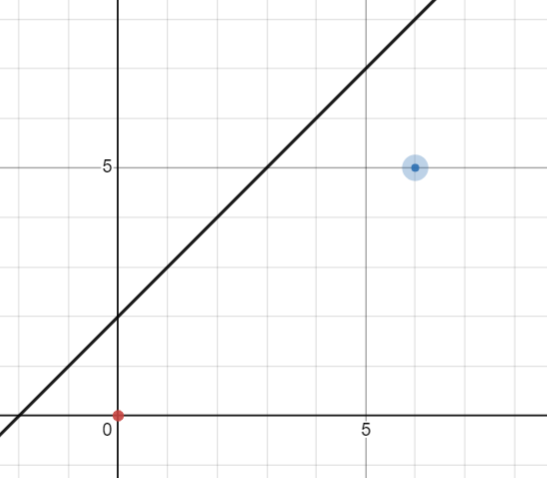
对于所有碰到这条线的,从第一次触碰开始反转,结束位置会变成 \((n,m)\) 关于 \(y=x+b\) 对称的点 \((m-b,n+b)\)。(如何推导?\(y=x+b\) 分别和 \(y=m,x=n\) 的交点的 \(x,y\) 坐标。)
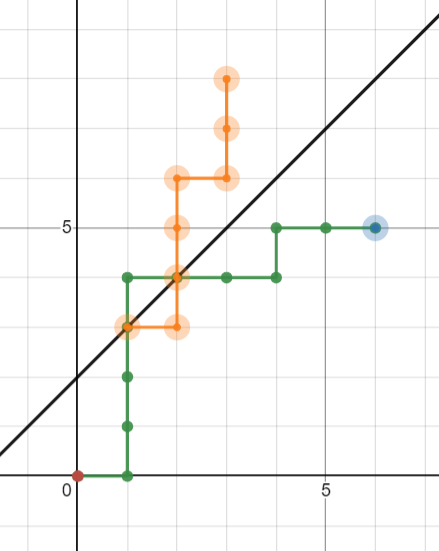
容易发现一条走到 \((m-b,n+b)\) 的线翻折之后对应的都是一条经过了 \(y=x+b\) 的路线。(这里指的是如果碰到线上一个点也算)
因此如果把 \(\dbinom{n+m}{n}\) 记为 \(p(n,m)\),表示 \((0,0)\) 到 \((n,m)\) 的路线个数,那么要求的答案等于 \(p(n,m) - p(m-b,n+b)\)。
如果有两条呢?\(y=x+b\) 和 \(y=x+c\)。
如果 \(b,c\) 都在终点的同一侧,可以认为是一个限制。否则形如下图:
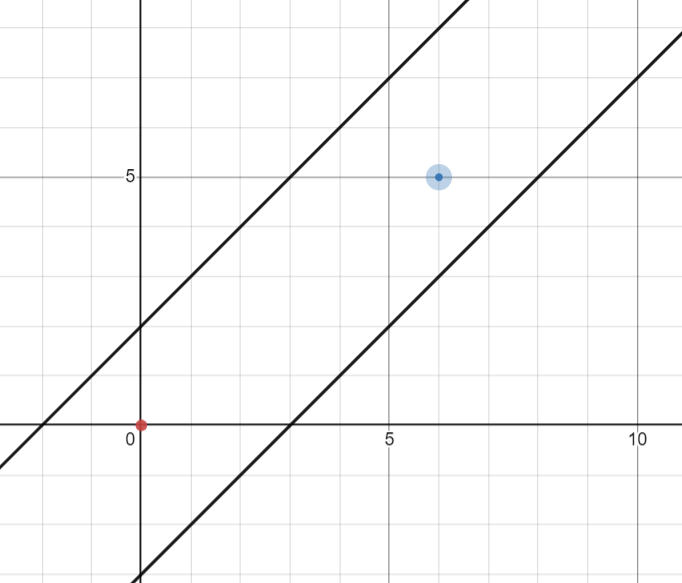
考虑答案为:总方案数 \(-\) 经过 \(y=x+b\) 的方案数 \(-\) 经过 \(y=x+c\) 的方案数 \(+\) 两个都经过的方案数。
这个说法有一定道理。但是有个问题,两个都经过的方案数怎么算?
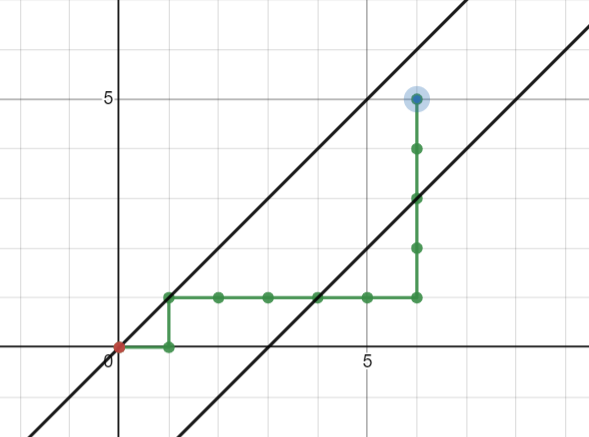
(默认 \(c<b\))
这个路线,如果先对 \(y=x+b\) 翻折再对 \(y=x+(2b-c)\)(也就是 \(x=c\) 关于 \(x=b\) 的对称点)翻折会变成:
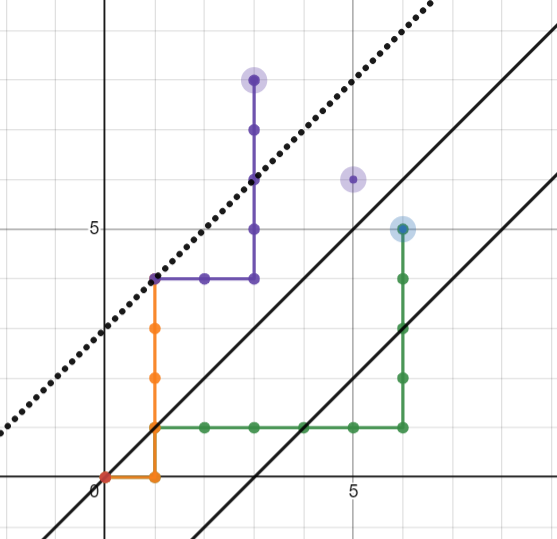
那么方案数为 \(p((n+b)-d,(m-b)+d),d=2b-c\)。
但是还有先到达 \(y=x+c\) 再到达 \(y=x+b\) 的路线。还有先到达 \(y=x+b\) 然后到达 \(y=x+c\) 再到达 \(y=x+b\) 的路线...
如果一条线依次经过了 \(y=x+b\),\(y=x+c\),\(y=x+b\),那么记其反射序列为 \(bcb\)。注意如果连续经过若干次 \(y=x+b\),只算一次。
类似地,定义终点依次关于 \(y=x+b\),\(y=x+c\),\(y=x+b\)(都是反射意义下的)对称得到的点的反射序列为 \(bcb\)。
考虑对于反射序列为 \(s\) 的点,有若干条从 \(0\) 到这个点的路径。对于每一条路径,建立一个一一映射,映射到的路线为:对于 \(s\) 上的序列,在第一次触碰到某一条线的时候,进行反射,得到的路线。
考虑在所有序列中,一个原序列映射到的位置:假设是 \(bcbcb\),那么会映射到 \(\emptyset, b,c,bc,cb,bcb,cbc,bcbc,cbcb,bcbcb\)。(注意,\(c\) 也会映射到,因为对于 \(c\) 上的一条路径,只关心第一次触碰到 \(c\) 的时刻)
那么我们需要统计的是:
\(\emptyset - b -c+bc+cb-bcb-cbc+bcbc-cbcb+...\)
这样每一个非空集元素的贡献都为 \(0\)。
容易发现一次反射最少超过 \(1\) 的偏移量,而如果反射到第一象限外就没有贡献,不需要再反射了。时间复杂度 \(O(\cfrac{n+m}{b-c})\)。
2 优化 DP
P3266
【题意】
\(dp_{1,0/1/2/.../m}=1\)
\(dp_{i,j}=\sum\limits_{k=0}^{j+1}dp_{i-1,k}(i>1)\)
求 \(\sum\limits_{j=0}^m dp_{n,j}\)
\(n,m\le 10^6\)
【分析】
这道题运用了 DP 的组合意义优化。计数类 DP 可以考虑。
先考虑转移,将其转化为 \(dp_{i,j} = dp_{i,j-1} + dp_{i-1,j+1}\)(当 \(j=0\) 的时候,\(dp_{i,j}=dp_{i-1,j}+dp_{i-1,j+1}\))。
这种方程是典型的格路计数类方程。我们来看看图:下图中从 \((1,0)\) 到 \((i,j)\) 的路径条数等于 \(dp_{i,j}\)。
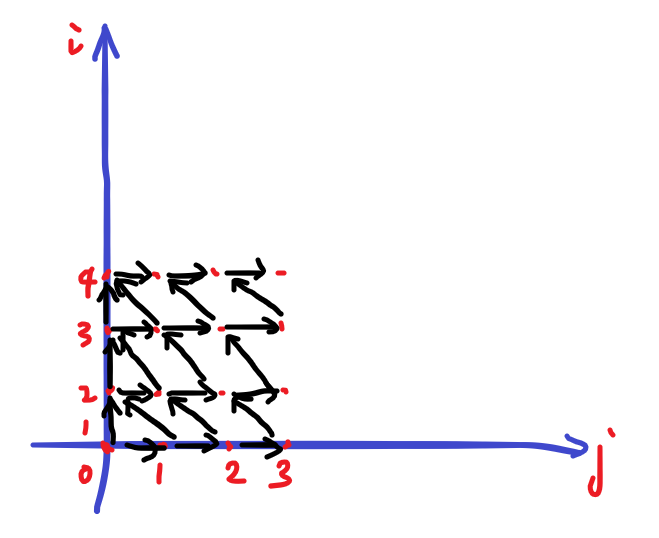
这个是往右走和左上走(先考虑一般情况)怎么办?为了更方便地运用格路计数有关结论,我们考虑对图做点变换:将 \(i\) 维度重新标号为从 \(0\) 开始,然后把第 \(i\) 行向右移动 \(i\) 格。
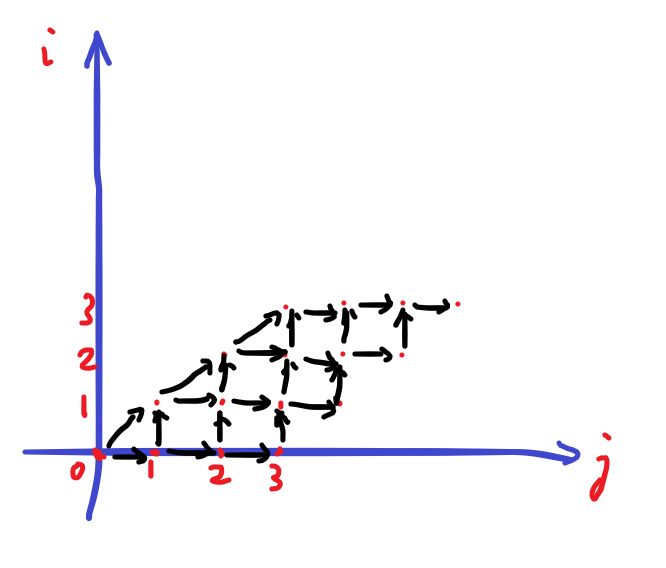
这样就大致符合格路计数的条件了。把左边的箭头改一改,然后画出两条不能经过的线,如下图:
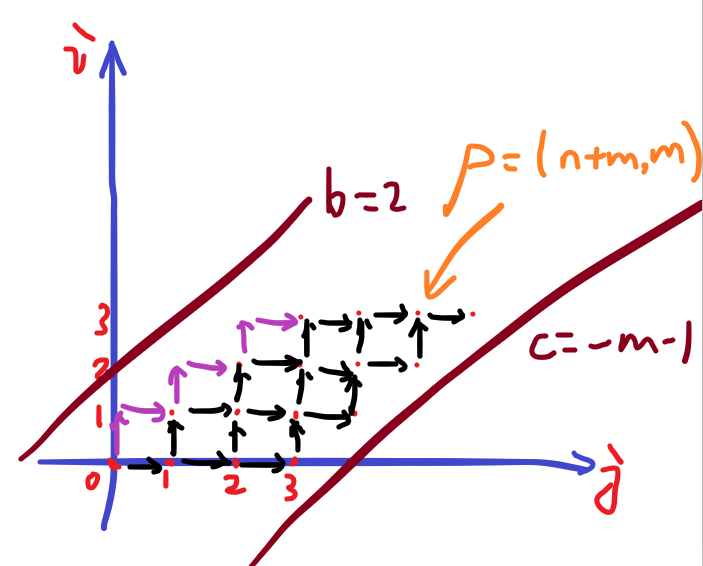
“这不板子吗!”
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
const int mod = 1e9+7;
int inv[3000010], jc[3000010];
int qpow(int n, int k) {
int ans=1;
while(k){if(k&1)ans=ans*n%mod;n=n*n%mod;k>>=1;}
return ans;
}
int p(int n, int m) {if(n<0||m<0)return 0; return jc[n+m]*inv[n]%mod*inv[m]%mod;}
int rv(int a, int b) {return 2*b-a;}//a 相对于 b 轴对称
pii pv(pii a, int b) {return make_pair(a.second - b, a.first + b);}
bool ok(pii pos) {return pos.first >= 0 && pos.second >= 0;}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n,m;cin>>n>>m;
int l=n+m,r=n; int b=2,c=-m-1; const int v = 3000000;jc[0]=inv[0]=1;
f(i, 1, v) { jc[i] = jc[i - 1] * i % mod; inv[i]=qpow(jc[i],mod-2); }
int ans = p(l,r); pair<pii, pii> ep = {pv({l,r}, b),pv({l,r}, c)};
int num = 0; int s=rv(c,b),t=rv(b,c);
while(ok(ep.first) || ok(ep.second)) {
++num; int mul = (num & 1 ? -1 : 1);
ans += p(ep.first.first,ep.first.second)*mul%mod; ans=(ans%mod+mod)%mod;
ans += p(ep.second.first,ep.second.second)*mul%mod; ans=(ans%mod+mod)%mod;
int tmpb=(num&1?t:s), tmpc=(num&1?s:t);
int tmpp=rv((num&1?b:c),s); int tmpq=rv((num&1?c:b),t);
ep.first=pv(ep.first,s);ep.second=pv(ep.second,t);
s=tmpp,t=tmpq,b=tmpb,c=tmpc;
}
cout<<ans<<endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
2.1 实现细节
- 终点变换之后坐标永远满足 \(x+y = n + m\)。也就是说,组合数相关的数组要处理到 \(n+ m\)。
- 维护四条线:\(b,c,s,t\),分别表示:这一轮上面那个作为对称轴的线是 \(y=x+s\),下一轮需要对称过去的那条线是 \(y=x+b\)(它是由一开始的 \(b\) 那条线经过若干次对称变换得到的);\(c,t\) 同理。(偶轮次,上面是 \(c\) 在做变换,因为反射序列为 \(bcbcbc...\))
- 取模的时候,因为乘了 \(-1\),需要按照负数取模方式。
gym104053J
还是一样,但是要求的是 \(y=-x+d\) 上所有点的路径个数和。
因为路径上点数是 \(O(b-c)\) 的,所以可以直接暴力对每个点求和,时间复杂度 \(O(n + m)\)。
3 模型推广
格路计数模型除了上面的反射容斥,还可以优化其他的 dp。
我们可以考虑给路径赋权值,计算起点到终点所有不同路径的权值和。如果并没有“不能过某一条线”的限制,计数可能变得很容易。
CF1821F Timber
【题意】
一条路的坐标范围是 \(0 \sim n + 1\),在上面种下 \(m\) 棵树,每棵树高度为 \(k\),种完之后进行砍伐,每棵树可以向左/右砍,一个坐标为 \(x\) 的树向左/右砍会分别倒在 \([x-k,x]\) 和 \([x,x+k]\) 范围内。合法的砍伐方式定义为:砍伐之后 \(0\) 和 \(n+1\) 这两个位置不存在倒树,任何一个位置不存在 \(\ge 2\) 棵倒树。求有多少种种树方式,使得存在合法的砍伐方式。
\(n,m,k \le 3\times 10^5\)
【分析】
首先我们考虑每一种种树方式的每一棵树,如果能往左倒就往左倒,否则往右倒,将其和倒树局面建立一个双射。然后 dp 这样的倒树局面的个数。
定义 \(dp_{i,j}\) 表示 \([i-k, i]\) 位置有一颗倒树,一共种了 \(j\) 棵树。
遍历到 \(i,j\),对于 \(t > k\):
初始 \(dp_{0,0} = 1\),求 \(\sum \limits_{i = 0}^ n dp_{i,m}\)。
首先有个 \(n^3\) 的 dp。
然后我们注意到 \(dp_{*,j}\) 的转移和 \(j\) 无关,并且就是向右移动,考虑生成函数。令 \(dp(x)\) 表示 \(dp_{*,j}\) 的生成函数,初始 \(j=0\),经过 \(m-1\) 次迭代,变成 \(dp_{*,m}\)。
迭代转移式子:
多项式快速幂可以做到 \(O(n \log n)\)。
但是能不能不用多项式?
考虑在格路上重新定义这个 dp 式子的含义。
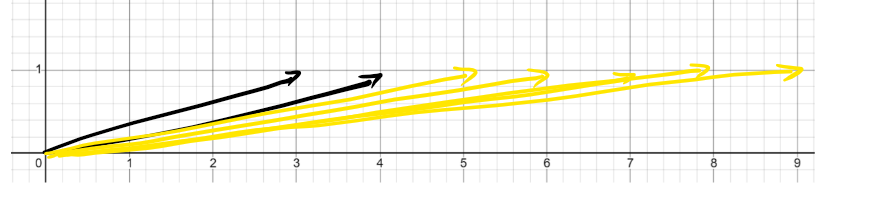
这是一个直接的转化,其中黑色权值为 \(2\),黄色权值为 \(1\)。某点 \((n,m)\) 的 dp 值等于从 \((0,0)\) 到它的所有路径权值积的和。
考虑把图建的好看些。对第 \(i\) 行,将横坐标做变换:\(x \rightarrow x-i(k+1)\),并且改变边的类型,如下图:
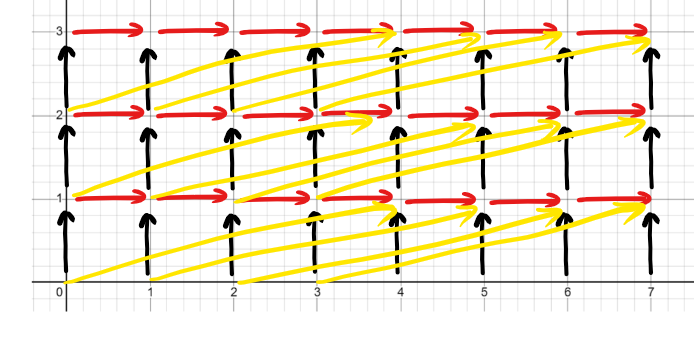
其中黑色的边权值为 \(2\),红色的边权值为 \(1\),黄色的边权值为 \(-1\)。
枚举走了多少次黄色边,剩下两个因为线性无关,所以可以直接得出来。注意第一行没有向右连边,分类讨论一下第一步走什么,得到一个 2 重循环的式子。更改变量枚举顺序之后可以预处理,能算,时间复杂度 \(O(n)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号