独立集问题

IOI2017国家集训队论文

定义

独立集问题有多种形式。为了方便描述，以下给出一些定义。

定义 2.1. 对于无向图 \(G = (V, E)\) 和点 \(u, v ∈ V\)，若 \((u, v) ∈ E\)，则称 \(u, v\) 相邻（adjacent）；定义点 \(v ∈ V\) 的邻域（neighborhood）为 \(V\) 中与 \(v\) 相邻的结点集合，记为 \(N(v)\)；另外，\(N_G(v)\)表示 \(v\) 在图 \(G\) 中的邻域。

定义 2.2. 点 \(v\) 的度（degree）\(deg(v)\) 定义为 \(N(v)\) 的大小，即 \(deg(v) = |N(v)|\)；另外，\(deg_G(v)\) 表示 v 在图 G 中的度。

定义 2.3. 无向图 \(G = (V, E)\) 的一个独立集（independent set）定义为 \(V\) 的一个子集，满足子集中的结点两两不相邻。形式化地，\(I\) 是 \(G\) 的一个独立集，当且仅当 \(I ⊆ V\) 且 \(∀u, v ∈ I， (u, v) \not\in E\)。

定义 2.4. 无向图 \(G = (V, E)\) 的一个最大独立集（maximum independent set）是指 \(G\) 中所含结点数 \(|I|\) 最多的独立集 \(I\)。

定义 2.5. 无向图 \(G = (V, E)\) 的独立数（independence number）定义为 \(G\) 的最大独立集 \(I\) 所
含的结点数 \(|I|\)，记为 \(α(G)\)。

定义 2.6. 无向图 \(G = (V, E)\) 在 \(S ⊆ V\) 上的导出子图（induced subgraph）定义为以 \(S\) 为点集，两端点都在 \(S\) 内的边为边集构成的图，记为 \(G[S]\)。

一般图的独立集问题

目前，解决一般图的大多数独立集相关的问题都不存在多项式时间的算法，只能用复杂度较优的指数级算法。
事实上，已有不少理论复杂度十分优秀的求图的最大独立集的算法，能够快速计算出上百阶的无向图的最大独立集，但这些算法实现往往过于复杂，难以应用到信息学竞赛中。笔者选择了一些相对高效又较易于实现的算法进行了研究。

基于极大独立集搜索的独立集算法

最朴素的搜索算法非常简单：用深度优先搜索枚举 \(V\) 的子集 \(I ⊆ V\)，即按一定顺序枚举每个点 \(v ∈ V\) 是否属于 \(I\)，一旦存在 \((u, v) ∈ E\) 使得 \(u, v ∈ I\)，就回溯。输出枚举的所有独立集 \(I\) 中，\(|I|\) 最大的一个。该算法的复杂度为 \(O(2^nm)\)，效率太低。

朴素的搜索算法效率太低，有没什么好的方法来优化呢？考虑极大独立集。不少有关独立集的组合优化问题都可以只考虑极大独立集，最大独立集问题就是这样一个例子：
定理 1：最大独立集都是极大独立集。

如果直接搜索极大独立集的话，效率是很低的，因为会搜到很多不是极大的独立集。
例如当 \(G\) 为 \(n\) 阶零图（没有边的图）时，显然 \(V\) 是 \(G\) 的唯一的极大独立集，然而朴素的搜索枚举了某个结点不属于极大独立集时，尽管不可能搜出极大独立集，但算法还会继续搜索下去，浪费了大量时间。
我们有一个优化策略：根据以下定理进行优化。
定理 2：对于极大独立集 \(I\)，不存在点 \(v\) 使得它和其邻域 \(n(v)\) 上所有点都不在 \(I\) 上。

那么我们引入 Bron 算法：
令目前确定在独立集内的点集为 \(R\)，可以加入独立集内（待定）的点集为 \(P\)，钦定不可以加入独立集内的点集（就是已经搜索完毕的点集）为 \(X\)。那么对于一个状态，\(P\cup X = V'\)，\(R\) 只是最后用于增加点的点集；\(V'\) 是还可供选择的点集。这点在之后的算法中可以发现。

\(\mathtt{Bron}(R,P,X)\) 返回的是当前状态下的最大独立集大小。

在函数内部，考虑新增一个加入独立集的点。对于任意 \(P \cup X\) 中节点 \(u\)，都有 \(P \cup (u \cup N(u))\) 中必然有一个点被选择。（由于任何已经被选择的点都已经把自己和邻域排除在 \(P \cup X\) 之外，所以不存在已经有点被选择的情况。继续搜索时，枚举这一个集合内的点，那么自然想到选取元素个数最少的一个 \(u\)。

选出 \(u\) 之后，对于所有 \(P \cup (u \cup N(u))\) 内节点 \(v\)，执行如下两个步骤：

• 求出选 \(v\) 的答案，也就是 \(\mathtt{Bron}(R \cup \{v\}, P - (v \cup N(v)), X - (v \cup N(v)))\)。
• 钦定不选 \(v\)（不会重复计算），\(P = P - \{v\}, X = X \cup \{v\}\)。（这样的话，下一次选 \(u\) 邻域内节点也不会再选到 \(v\)，因为 \(u\) 邻域上点的邻域不一定包含 \(v\)，不这样做可能会选到）

递归终点：
当 \(P = X = ∅\) 的时候，所有可选节点都在 \(R\) 中，用 \(R\) 更新答案。当 \(P = \emptyset\) 的时候，如果 \(X \neq \emptyset\)，那么令 \(k \in X\)，那么它的邻域内没有选择任何一个节点，否则这个点选择过的话会把 \(k\) 删掉。并且你无法再添加任何节点了。这时候你肯定没有搜索到极大独立集，直接返回即可。
当 \(X = \emptyset\) 的时候，\(P\) 一定也为 \(\emptyset\)。

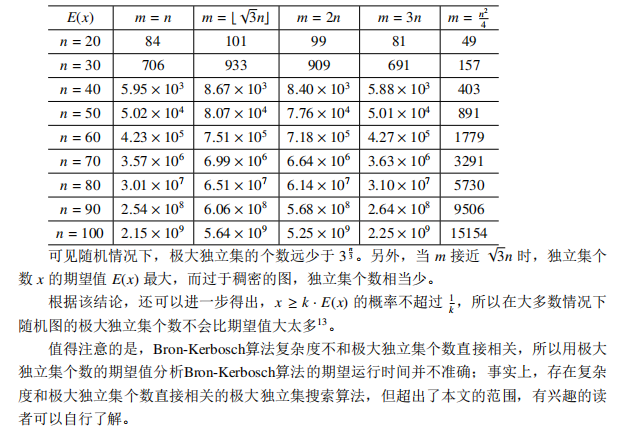
时间复杂度：递归调用层数 \(O(3^{\frac{n}{3}})\)，证明很复杂，结论背下来即可。

另外，一张图的极大独立集也是 \(O(3^{\frac{n}{3}})\) 的。造 \(k\) 个 \(k\) 元环可以达到上界，并且 \(k = 3\) 的时候，达到最大上界（实数范围上界在 \(k = e\) 取到）。

由于该算法基于极大独立集，也可以求解最大正权独立集。

对于随机图：

CF1767E

\(n \le 40\)。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
int n,m;
int c[300010],x[44];
int g[44];  //状压
void add(int x, int y) {g[x] |= (1ll << y); g[y] |= (1ll << x);}
int ans=0,sum=0;
void print(int t){
    string s;cin>>s;
    f(i,0,m-1){s+=char((t&1)+'0');t>>=1;}
    cout<<s<<endl;
}
void bron(int R,int P,int X){
    if(P==0){
        int tmp=0;
        f(i,0,m-1)if((R>>i)&1)tmp+=x[i]; 
        cmax(ans,tmp);  
        return;
    }
    int mn=inf,ch=0;
    f(i,0,m-1){
        if((P>>i)&1 || (X>>i)&1){
            int gs=(P&(g[i]|(1ll<<i)));
            int nt=__builtin_popcountll(gs);
            if(nt != 0 && nt<mn){mn=nt;ch=i;}
        }
    }
    int ly = (P&(g[ch]|(1ll<<ch)));
    f(i,0,m-1){
        if((ly >> i) & 1) {
            int lx = (g[i]|(1ll<<i));
            int flx = ~(lx);
            bron(R | (1ll << i), P & flx, X & flx);
            P -= (1ll<<i);
            X |= (1ll<<i);
        }
    }
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    //time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    cin>>n>>m;
    f(i,0,n-1){cin>>c[i];c[i]--;}
    f(i,0,m-1){cin>>x[i];sum+=x[i];}
    f(i,0,n-2){add(c[i],c[i+1]);}
    int R=0,P=0,X=0;
    f(i,0,m-1){
        if(c[0]==i||c[n-1]==i||((g[i]>>i)&1));
        else P|=(1ll<<i);
    }
    f(i,0,m-1)g[i]&=P;
    bron(R,P,X);
    cout<<sum-ans<<endl;
    //time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}

trick：可以用 R &= ~P 来执行 \(R -= P\)。

基于折半搜索的独立集算法

考虑折半查找的思想。
如果把一整张图分成两个部分，前 \(n/2\) 个点和后 \(n/2\) 个点。分别将这两个点集记为 \(mask_1, mask_2\)。对于 \(mask_1\) 和 \(mask_2\) 的每个子集 \(S\)，状态压缩处理出 \(G[S]\) 的最大独立集。
然后考虑枚举 \(mask_1\) 里选了哪些点，对这些点的邻域取并集之后，没有取到的点（在 \(mask_2\) 中）就是可选择的点集。这时候我们需要查询这个点集的所有子集的最大独立集的最大值。总共 \(O(2^{n/2})\) 次查询。怎么办？
使用高维前缀和处理子集信息查询问题。
想象高维空间上的几何体得到，令 \(m = n/2\)，那么 \(m\) 维空间中，如果做前缀和，那么 \(s_{x_1,...,x_m}\) 就是 \(x_1...x_m\) 的所有子集的权值和。
这个前缀和，除了容斥求解，还可以这样做：对每个维度分别求一次前缀和。
令值域为 \([1,k]\)，那么时间复杂度 \(O(m \times k^m)\) 可以预处理所有集合的子集和。其中 \(k^m\) 是高维空间容量。

for(int i=1;i<=n;++i)
{
    for(int j=1;j<=m;++j)
    {
        for(int k=1;k<=p;++k)
        {
            a[i][j][k]+=a[i-1][j][k];
        }
    }
}
for(int i=1;i<=n;++i)
{
    for(int j=1;j<=m;++j)
    {
        for(int k=1;k<=p;++k)
        {
            a[i][j][k]+=a[i][j-1][k];
        }
    }
}
for(int i=1;i<=n;++i)
{
    for(int j=1;j<=m;++j)
    {
        for(int k=1;k<=p;++k)
        {
            a[i][j][k]+=a[i][j][k-1];
        }
    }
}

对于子集求和问题，\(k=2\)，\(0/1\) 分别表示选不选。

for(int i = 1; i <= m; i++) {
    for(int j=0;j<(1<<w);++j)//求每个维度的前缀和
    {
        if(j&(1<<i))s[j]+=s[j^(1<<i)]; 
    }
}

总时间复杂度 \(O(2^{n/2} \times n^2)\)。可以处理负权。

树和基环树的最大（权）独立集

树的最大独立集问题，不能黑白染色取黑或者白，因为只是保证邻域内必须选一个，没说相邻的也要选。

考虑树形 dp。\(dp_{i,0/1}\) 第 \(i\) 个选不选，子树内最大独立集。

基环树，如下图，环上面每个点是一棵树的根。

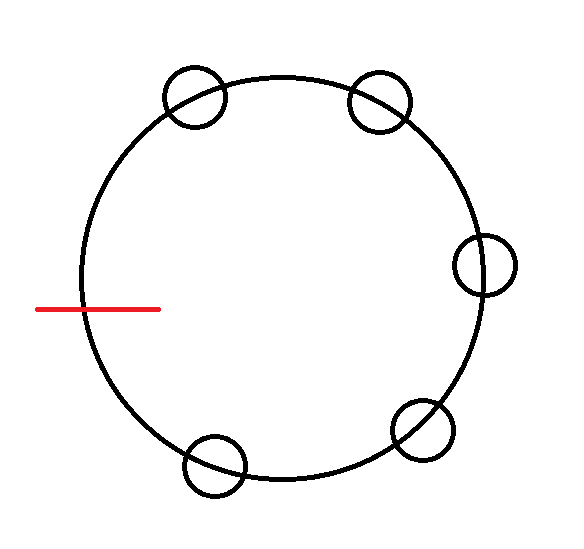
考虑先把每棵树的答案算出来，然后环上的点标号，\(f_{i, 0/1,0/1}\) 表示第 \(i\) 个点选不选，第一个点选不选。
然后最后一个点注意一下就好了。