数学推导比较多。但是充斥着对称美。
单调队列/斜率优化,都是决策单调性优化。这篇主要说四边形不等式优化。
还没写完。
基本定义
四边形不等式:对于二元函数 w x , y w x , y a ≤ b ≤ c ≤ d a ≤ b ≤ c ≤ d w a , b + w c , d ≥ w a , c + w b , d w a , b + w c , d ≥ w a , c + w b , d 相交 ≤ ≤ ),那么称 w i , j w i , j
等价转化
对于二元函数 w x , y w x , y 任意 a < b a < b w a , b + 1 + w a + 1 , b ≥ w a , b + w a + 1 , b + 1 w a , b + 1 + w a + 1 , b ≥ w a , b + w a + 1 , b + 1 w i , j w i , j
定义①通常用来推出某些结论,定义②通常用来证明某个二元函数满足四边形不等式。
证明等价:c > a c > a c = a + 1 c = a + 1 w a , c + 1 + w a + 1 , c ≥ w a , c + w a + 1 , c + 1 w a , c + 1 + w a + 1 , c ≥ w a , c + w a + 1 , c + 1
w a , c + 1 + w a + 1 , c ≥ w a , c + w a + 1 , c + 1 w a + 1 , c + 1 + w a + 2 , c ≥ w a + 1 , c + w a + 2 , c + 1 w a , c + 1 + w a + 1 , c ≥ w a , c + w a + 1 , c + 1 w a + 1 , c + 1 + w a + 2 , c ≥ w a + 1 , c + w a + 2 , c + 1
加起来得到:
w a , c + 1 + w a + 2 , c ≥ w a , c + w a + 2 , c + 1 w a , c + 1 + w a + 2 , c ≥ w a , c + w a + 2 , c + 1
以此类推,得到对于任意 a ≤ b ≤ c a ≤ b ≤ c
w a , c + 1 + w b , c ≥ w a , c + w b , c + 1 w a , c + 1 + w b , c ≥ w a , c + w b , c + 1
故技重施。对于 c < m a x n c < m a x n
w a , c + 2 + w b , c + 1 ≥ w a , c + 1 + w b , c + 2 w a , c + 2 + w b , c + 1 ≥ w a , c + 1 + w b , c + 2
加起来得到:
w a , c + 2 + w b , c ≥ w a , c + w b , c + 2 w a , c + 2 + w b , c ≥ w a , c + w b , c + 2
以此类推,得到定义①。
矩阵形式
对于 N × M N × M A A
∀ i 1 ≤ i 2 , j 1 ≤ j 2 , A i 1 , j 1 + A i 2 , j 2 ≤ A i 1 , j 2 + A i 2 , j 2 ∀ i 1 ≤ i 2 , j 1 ≤ j 2 , A i 1 , j 1 + A i 2 , j 2 ≤ A i 1 , j 2 + A i 2 , j 2
那么称 A A
A i , j + A i + 1 , j + 1 ≤ A i , j + 1 + A i + 1 , j ⇒ A i , j + 1 − A i , j ≥ A i + 1 , j + 1 − A i + 1 , j A i , j + A i + 1 , j + 1 ≤ A i , j + 1 + A i + 1 , j ⇒ A i , j + 1 − A i , j ≥ A i + 1 , j + 1 − A i + 1 , j
也即,A ∗ , j A ∗ , j A ∗ , j + 1 A ∗ , j + 1 增长更快 ,如果第 i i j j ∀ i 1 > i , j 1 < j ∀ i 1 > i , j 1 < j A i 1 , j 1 ≤ A i 1 , j A i 1 , j 1 ≤ A i 1 , j
这就是四边形不等式的本质,相交小于等于还是大于等于包含不重要,只是推出了一个矩阵的单调形式,放弃了很多没用的矩阵。
应用类型 I
考虑如下 dp 转移式子:
f i = min 0 ≤ j < i { f j + v j , i } f i = min 0 ≤ j < i { f j + v j , i }
其中 v v 若对于 i i p p k < p k < p i ′ > i i ′ > i p p k < p k < p
证明:
f p + v p , i ≤ f k + v k , i v k , i + v p , i ′ ≤ v k , i ′ + v p , i f p + v p , i ≤ f k + v k , i v k , i + v p , i ′ ≤ v k , i ′ + v p , i
相加得到
f p + v p , i ′ ≤ f k + f k , i ′ f p + v p , i ′ ≤ f k + f k , i ′
不难得到推论,p i p i
那么如何求出整个 DP 数组呢?可以从 O ( n 2 ) O ( n 2 ) O ( n log n ) O ( n log n ) 二分栈 。
我们考虑 p p p i p i i i
一开始,计算出 f 0 f 0 p p 0000000000 0000000000
若干个数求完之后,数组可能变成了:0000111122 0000111122 0 ∼ 2 0 ∼ 2 p 3 p 3 3 3 f 3 f 3
考虑如何添加 f 3 f 3 3 3 0000113333 0000113333 O ( n 2 ) O ( n 2 )
考虑维护颜色段 ,类似珂朵莉树思想。用一个集合,元素为 ( l , r , k ) ( l , r , k ) k k n n n n
实现方面,用 deque。或者 list。后者,比较安全,但是不能随机访问。(这里不需要随机访问。)
应用类型 II
考虑如下 DP 转移式:
d p i , j = min 0 ≤ k < i { d p k , j − 1 + v k + 1 , i } d p i , j = min 0 ≤ k < i { d p k , j − 1 + v k + 1 , i }
其中 v v j j d p i , j d p i , j
先介绍另一种方法,然后考虑这两种方法有什么不一样。这种方法叫分治 。没错,分治博客里面有一个决策单调性的例题。现在知道了原理。(变成套路了捏)
考虑 s o l v e ( l , r , x , y ) s o l v e ( l , r , x , y ) d p l ∼ r , j d p l ∼ r , j ( x , y ) ( x , y ) m i d m i d k k s o l v e ( l , m i d − 1 , x , k ) , s o l v e ( m i d + 1 , r , k , y ) s o l v e ( l , m i d − 1 , x , k ) , s o l v e ( m i d + 1 , r , k , y )
考虑时间复杂度。虽然带端点,但是端点计算次数是 O ( 区 间 数 ) = O ( n ) O ( 区 间 数 ) = O ( n ) O ( n l o g n ) O ( n l o g n )
不同之处
第二种情况,是没有用到左边的 dp 值,直接先算出了右边的 dp 值的。而当遇到第一种情况那样,dp 值后来也是决策的时候,就不管用了。
应用类型 III
考虑如下转移:
f i , j = min i ≤ k < j { f i , k + f k + 1 , j + w i , j } f i , j = min i ≤ k < j { f i , k + f k + 1 , j + w i , j }
若满足以下三个条件 :
w w f i , i = w i , i = 0 f i , i = w i , i = 0 ∀ a ≤ b ≤ c ≤ d , w a d ≥ w b c ∀ a ≤ b ≤ c ≤ d , w a d ≥ w b c
那么 f f
证明:要证明对于任意 i < j i < j f i , j + 1 + f i + 1 , j ≥ f i , j + f i + 1 , j + 1 f i , j + 1 + f i + 1 , j ≥ f i , j + f i + 1 , j + 1
首先证明 j = i + 1 j = i + 1 j = i + 1 j = i + 1 f i , j + 1 + f i + 1 , j = f i , i + 2 + f i + 1 , i + 1 = f i , i + 2 f i , j + 1 + f i + 1 , j = f i , i + 2 + f i + 1 , i + 1 = f i , i + 2 = f i , i + 1 + f i + 1 , i + 2 = f i , i + 1 + f i + 1 , i + 2 f i , i + 2 f i , i + 2 i i i + 1 i + 1
决策点是 i i f i , i + 2 = f i , i + f i + 1 , i + 2 + w i , i + 2 = f i + 1 , i + 2 + w i , i + 2 f i , i + 2 = f i , i + f i + 1 , i + 2 + w i , i + 2 = f i + 1 , i + 2 + w i , i + 2 f i , i + 1 = w i , i + 1 ≤ w i , i + 2 f i , i + 1 = w i , i + 1 ≤ w i , i + 2
决策点是 i + 1 i + 1
然后证明,如果对于 j − i < k j − i < k j − i = k j − i = k
a ≤ b ≤ c ≤ d , c − a < k , f a , d + f b , c ≥ f a , c + f b , d a ≤ b ≤ c ≤ d , c − a < k , f a , d + f b , c ≥ f a , c + f b , d
做好了准备工作之后,我们考虑证明对于 j − i = k j − i = k f i , j + 1 + f i + 1 , j ≥ f i , j + f i + 1 , j + 1 f i , j + 1 + f i + 1 , j ≥ f i , j + f i + 1 , j + 1
考虑 x , y x , y f i , j + 1 , f i + 1 , j f i , j + 1 , f i + 1 , j i ≤ x ≤ j , i < y < j i ≤ x ≤ j , i < y < j
考虑 x , y x , y
x ≤ y x ≤ y i < x ≤ j , i < y < j i < x ≤ j , i < y < j y , x y , x f i , j , f i + 1 , j + 1 f i , j , f i + 1 , j + 1 f f f i , j + 1 + f i + 1 , j = f i , x + f x + 1 , j + 1 + w i , j + 1 + f i + 1 , y + f y + 1 , j + w i + 1 , j f i , j + 1 + f i + 1 , j = f i , x + f x + 1 , j + 1 + w i , j + 1 + f i + 1 , y + f y + 1 , j + w i + 1 , j f i , j + f i + 1 , j + 1 ≤ f i , x + f x + 1 , j + w i , j + f i + 1 , y + f y + 1 , j + 1 + w i + 1 , j + 1 f i , j + f i + 1 , j + 1 ≤ f i , x + f x + 1 , j + w i , j + f i + 1 , y + f y + 1 , j + 1 + w i + 1 , j + 1 w w w i , j + w i + 1 , j + 1 ≤ w i , j + 1 + w i + 1 , j w i , j + w i + 1 , j + 1 ≤ w i , j + 1 + w i + 1 , j f x + 1 , j + f y + 1 , j + 1 ≤ f x + 1 , j + 1 + f y + 1 , j f x + 1 , j + f y + 1 , j + 1 ≤ f x + 1 , j + 1 + f y + 1 , j x + 1 ≤ y + 1 ≤ j < j + 1 , j − ( x + 1 ) < k x + 1 ≤ y + 1 ≤ j < j + 1 , j − ( x + 1 ) < k x > y x > y
因此 f f
推论:对于任意 i < j i < j p i , j − 1 ≤ p i , j ≤ p i + 1 , j p i , j − 1 ≤ p i , j ≤ p i + 1 , j
证明:考虑右式,设 q = p i , j q = p i , j i < i + 1 ≤ k ≤ p i < i + 1 ≤ k ≤ p f i , p + f i + 1 , k ≥ f i , k + f i + 1 , p f i , p + f i + 1 , k ≥ f i , k + f i + 1 , p f i + 1 , j f i + 1 , j k k p p f i + 1 , k + f k + 1 , j + w i + 1 , j − f i + 1 , p − f p + 1 , j − w i + 1 , j ≥ 0 f i + 1 , k + f k + 1 , j + w i + 1 , j − f i + 1 , p − f p + 1 , j − w i + 1 , j ≥ 0
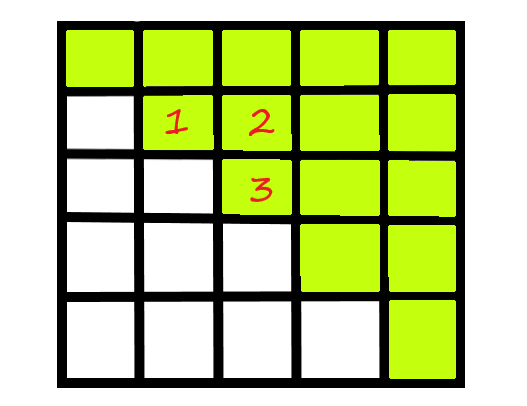
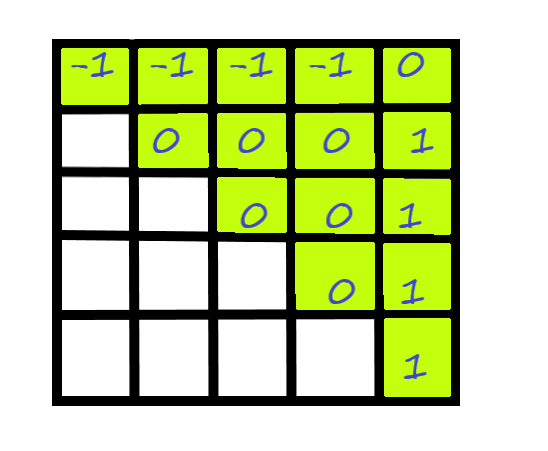
因此考虑一个矩阵 p p 1 1 ≤ ≤ 2 2 ≤ ≤ 3 3
因此在计算一个点的时候,缩小了枚举范围。事实上,把 O ( n 3 ) O ( n 3 ) O ( n 2 ) O ( n 2 ) p i , j p i , j p i + 1 , j − p i , j − 1 + 1 p i + 1 , j − p i , j − 1 + 1 + 1 + 1 − 1 − 1
容易发现,因为 p i , j ≤ n p i , j ≤ n O ( n 2 ) O ( n 2 )



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通