生成函数

《组合数学》 2.2；2015 集训队论文 金策
本文中记法：\(C_i\) 表示原序列的第 \(i\) 项，\(C(x)\) 表示 \(C\) 序列对于 \(x\) 的形式幂级数。\([x^k] \mathrm{poly }x\) 表示式子中 \(k\) 次项系数。这里面没有其他方括号，所以直接用方括号了。

注意在 OGF 内 \([x^k] C(x) = C_k\)，但是在 EGF 内 \([x^k] C(x) = \cfrac{C_k}{k!}\)。

定义

生成函数，也就是母函数，可以求数列的通项公式，是探究数列的强有力的工具。

普通生成函数

是一种形式幂级数，意思是每一项的系数是关心的，\(x\) 的取值范围不重要，只是形式的参数，没有实际意义，也可以任意假定敛散性。

对于数列 \(C_0,C_1,C_2,...\)，构造函数

\[C(x) = C_0 x^0 + C_1 x^1 + ... \]

生成函数和原数列一一对应。
其中数列的长度可以有限，也可以无限。

我们可以通过递推式求出生成函数，然后进行封闭形式的组合，然后展开。下面有两个例子：

河内塔问题

递推式我们求出来了是 \(H_i = 2H_{i-1} + 1\)。
特别地 \(H_0 = 0\)。
考虑 \(H\) 的生成函数 \(G(x) = H_0 x^0 + H_1 x^1 + ...\)
考虑

\[H_1 x = (2H_0 + 1) x \\ H_2 x^2 = (2H_1 + 1) x^2 \\ ... \]

左右两边分别求和，得到
\(G(x) = 2xG(x) + (x + x^2 + ...)\)
我们有 \(\cfrac{1}{1-x} = (1 + x + x^2 + ...)\)，这个式子对生成函数的转化有极大用处。注意这个式子成立的条件是 \(|x| \le 1\)，但是在这里我们可以将 \(x\) 视为任何数，默认 \(x^\inf\) 收敛为 \(0\)。

继续转化， \((1-2x)G(x) = x \times \cfrac{1}{1-x}\)，\(G(x) = \cfrac{x}{(1-x)(1-2x)}\)。

现在母函数求出来了，考虑怎么求出原数列。目标是还原成接近 \(\cfrac{1}{1-x}\) 的形式，从而能够回去。

考虑 \(G(x) = \cfrac{A}{1-x} + \cfrac{B}{1-2x}\)，待定系数法得 \(A = -1,B= 1\)。于是 \(G(x) = \cfrac{1}{1-2x} - \cfrac{1}{1-x} = (1+2x+2^2x^2+...) - (1+x+x^2+...)\)

因此 \(H_i = 2^i - 1\)。

斐波那契数列

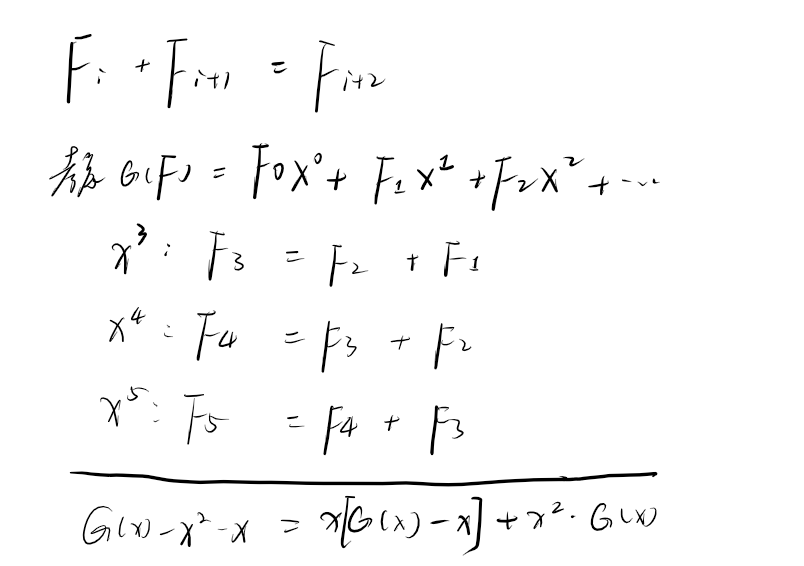
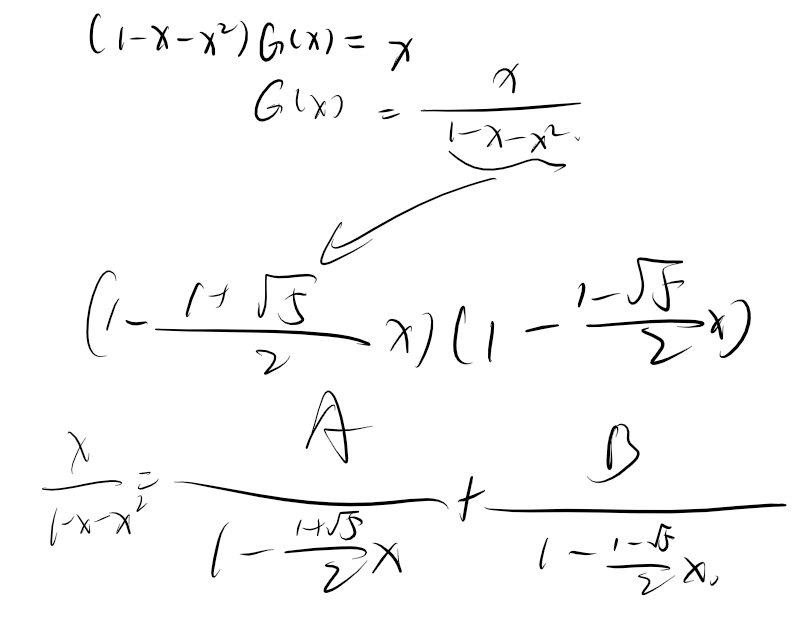
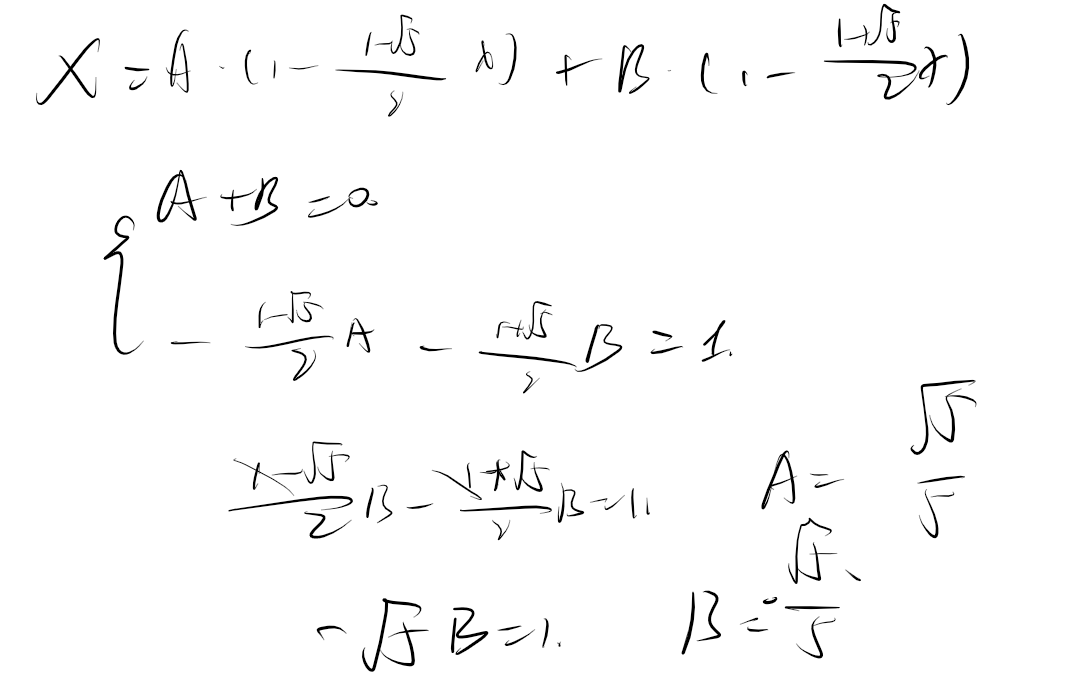
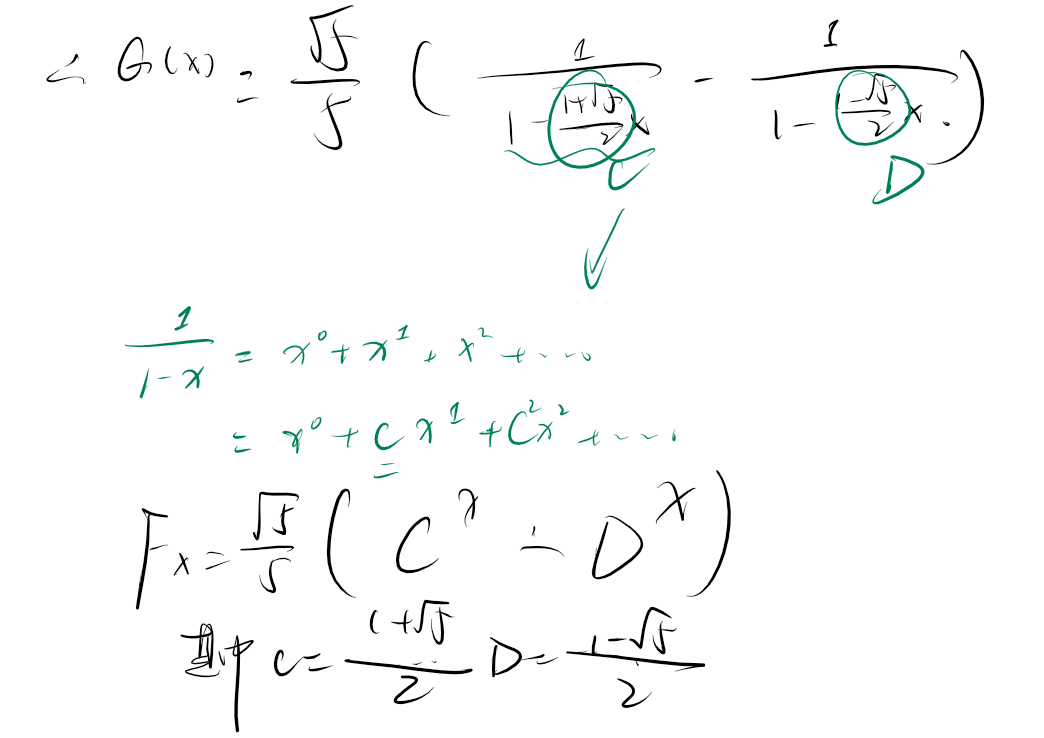
注意，最后要尽可能划到 \(\cfrac{?}{1-x}\) 的样子，其中 \(?\) 是乘法，保留在原函数的通项公式中。

斐波那契一些常用性质要知道，还有一个 gcd 的是 \(\gcd(F_n,F_m) = F_{gcd(n,m)}\)。

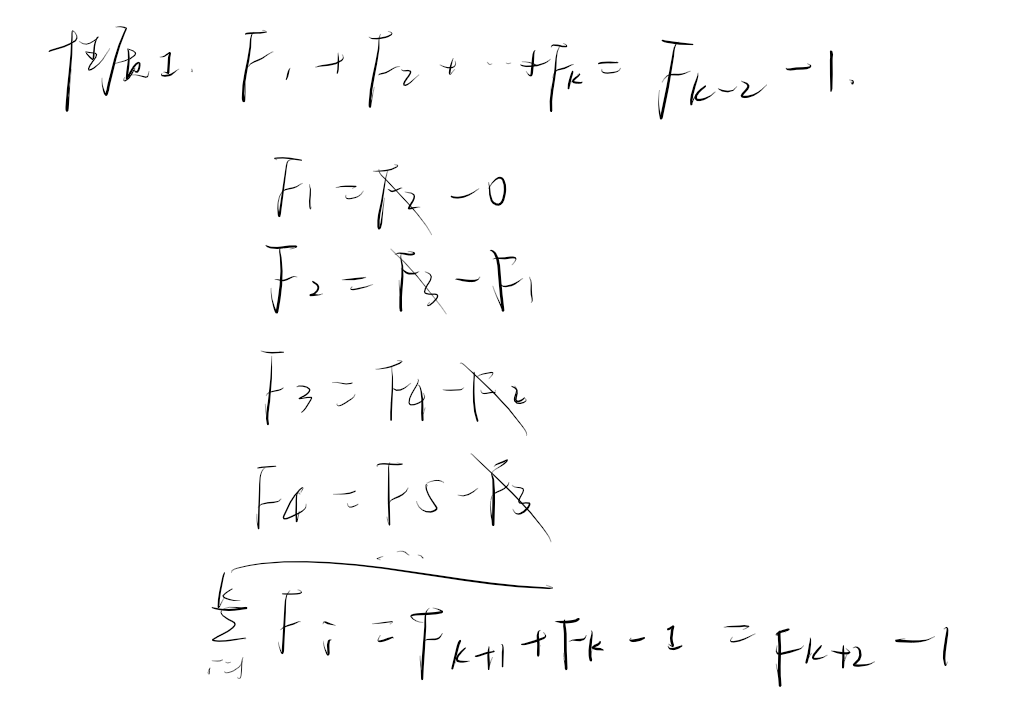
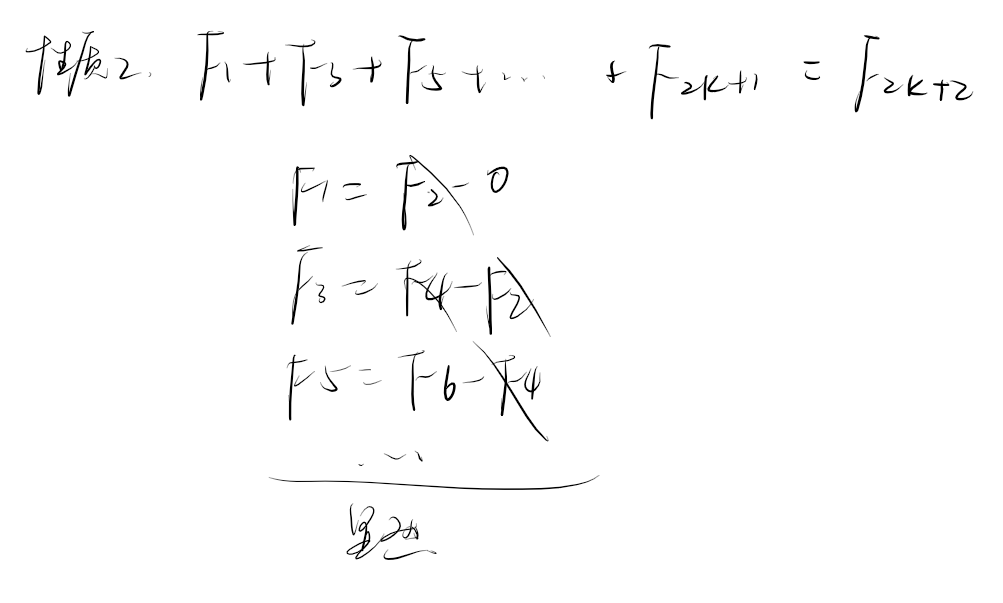
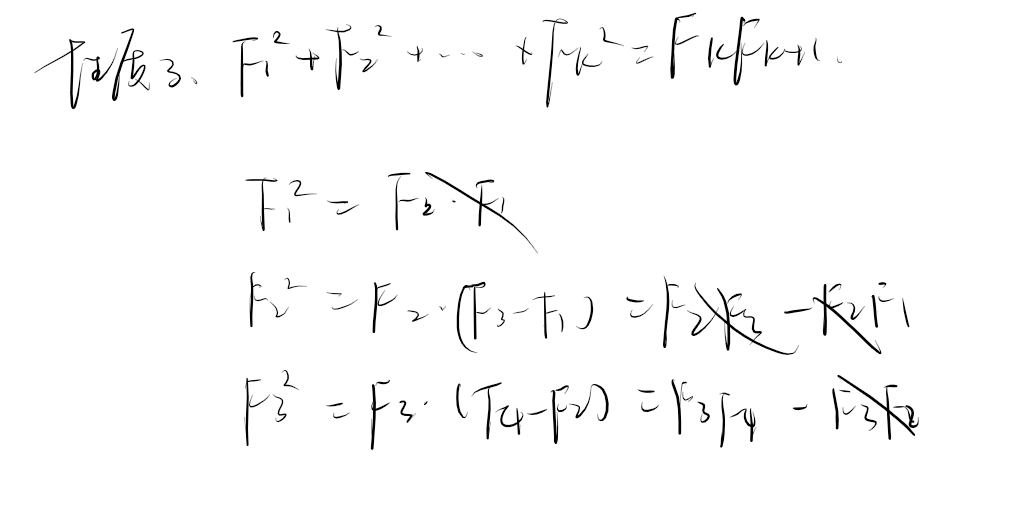
一些经典的变换：\(m^0x^k+m^1x^{k+1}+m^2x^{k+2}+... = \cfrac{x^k}{1-mx}\)。

指数型生成函数

定义为

\[C(x) = \sum_{i \ge 0} C_i \times \cfrac{x^i}{i!} \]

具体什么用，第一是可能 OGF 不能导出某个封闭形式（完全发散），第二是下面说的关于有没有标号的问题。

组合对象

组合计数问题中，我们把满足某一个性质的某一类图/树/串等的集合定义为组合对象 \(A\)，其中每个对象 \(a \in A\) 都被定义了一个大小 \(size(a) \in \N\)，可能代表节点数量、序列长度等。对于某一个固定的 \(n\)，满足 \(size(a) = n\) 的对象 \(a\) 的数量是有限的，记为 \(A_n\)。我们的任务通常是求 \(A_n\) 的数值。

根据不同问题的要求，组合对象可以分成有标号和无标号两类。

考虑两类无标号对象 \(A, B\)，定义 \(A(x)\) 为 \(A_n\) 的 OGF，\(B(x)\) 为 \(B_n\) 的 OGF。如果 \(A, B\) 交集为空，那么 \(A \cup B\) 的 OGF 是 \(A(x) + B(x)\)。

考虑他们的笛卡尔积 \(D = A \times B\)，其中每一个 \(D\) 中的元素 \(d\) 都是一个二元组 \((a, b)\)，其中 \(a \in A, b \in B\)，并且定义 \(size(d) = size(a) + size(b)\)。那么有

\[D_k = \sum \limits_{i + j = k} A_i B_j \]

于是 \(D\) 的 OGF 是 \(D(x) = A(x) \times B(x)\)。

考虑两类有标号对象 \(A, B\)，对于交集，公式不变，但是对于笛卡尔积，两个对象进行合并的时候重新赋标号，要求两个对象内部标号大小不变化。那么需要乘以组合数：

\[D_k = \sum \limits_{i + j = k} A_iB_j \cfrac{k!}{i!j!} \]

我们断言这样的积起来的 \(D\) 的 EGF 满足 \(D(x) = A(x) \times B(x)\)。

考虑 \([x^k]A(x) \times B(x)\) 的取值。它等于 \(\sum \limits_{i + j = k} A_i \cfrac{1}{i!} B_j \cfrac{1}{j!}\)。

而 EGF 要求 \([x^k]A(x) \times B(x) = D_k \times \cfrac{1}{k!}\)，于是满足了。

不是说所有有标号问题的生成函数结合都是这样的，只是合并的时候重新标号才是这样的，如果没有重新标号，不是这样的。这点要注意一下。

乘法逆元

对于多项式，\(\epsilon = 1\)。当 \(A(x)B(x) = 1\) 的时候，称 \(A(x), B(x)\) 互为乘法逆元，可以写作 \(A(x) = B(x)^{-1} = 1 / B(x)\)。

例如

\[\cfrac{1}{1 - x} = 1 + x + x^2 + x^3 + ... \]

这个等式可以用来做前缀和。对于数列 \(a_0, a_1, ...\)，定义 \(s_n = \sum \limits_{i = 0}^n a_i\)，那么 \(S(x) = \cfrac{1}{1-x} A(x)\)。

就是你把展开的东西乘一下，原来每一项系数都会贡献到后面。

还有一个式子

\[\cfrac{1}{(1-x)^{n+1}} = \sum \limits_{i \ge 0} \dbinom{n + i}{n} x^i \]

这可以用插板法进行理解，对于展开形式出现组合数的式子可以这样化为封闭形式。

关于第一个方法，是一个往后贡献的巧妙方法很常见，例如一个式子：

\[f_i = \sum \limits_{j > 0, j \in D} f_{i - j} \]

这个式子你考虑生成函数是什么，其实你可以定义 \(D(x) = \sum \limits_{i > 0, i \in D}x^i\) 然后等式右边 \(\sum \limits_{i \ge 0} \sum \limits_{j > 0, j \in D} f_{i - j}\) 可以认为是 \(F(x) \times D(x)\)。

回到主题，接下来看乘法逆元怎么求。

\(A(x)\) 存在乘法逆元的充要条件是 \(A(x)\) 的常数项存在逆元，因为 \([x^0]A(x) [x^0]B(x) =1\)。

然后对于 \(i \ge 1\)，需要 \(\sum \limits_{t = 0}^i A^tB^{i-t} = 0\)。

采用牛顿迭代法。

首先求得 \(A(x)\) 的常数项逆元 \(b\)，并且令 \(B(x)\) 的初始值为 \(b\)。

假设已经求得满足

\[A(x)B(x) \equiv 1(\bmod x^n) \]

这个 \(\bmod\) 有两个含义，一个是取前 \(n\) 项满足，还有一个是如果带入合适的 \(x\)，该式子是一个数值上成立的同余方程。

那么

\[A(x)B(x) - 1 \equiv 0 (\bmod x^n) \\ (A(x)B(x) - 1)^2 \equiv 0(\bmod x^{2n}) \\ A(x)(2B(x)-B(x)^2A(x)) \equiv 1(\bmod x^{2n}) \]

我们只需要算出 \(2B(x) - B(x)^2 A(x)\) 并且赋值给 \(B(x)\) 即可。

时间复杂度为，\(T(n) = T(n/2) + O(n \log n) = O(n \log n)\)。

序列计数

你有若干种颜色不同的面条，其中大小为 \(i\) 的共有 \(a_i\) 种。用面条不重不漏铺满长度为 \(n\)，一共有几种方法？

枚举使用的骨牌数量 \(k\)，设 \(A(x) = \sum \limits_{i \ge 0}a_ix^i\)，那么显然有 \(ans = [x^n]\sum\limits_{k\ge 0}A(x)^k = [x^n] \cfrac{1}{1 - A(x)}\)。

求 \(1 - A(x)\) 的乘法逆元，可以得到答案。

一般地，对于一类组合对象 \(A\)，由任意个 \(A\) 中元素组成的新对象 \(B\) 的生成函数为

\[B(x) = \cfrac{1}{1 - A(x)} \]

这就是这个式子的意义。

对数和指数运算

形式导数

对于 \(A(x) = \sum \limits_{i \ge 0}a_ix^i\)，定义其形式导数为

\[A'(x) = \sum \limits_{i \ge 1} i a_i x^{i - 1} \]

这个导数就是正常把多项式看成函数的导数，其是一个多项式，但是看成关于 \(x\) 的函数之后确实是一个导数。所以其运算律和普通导数一样（其实只是把函数写成多项式，多项式的所有运算和函数的效果都一样，没改变什么别的，自然是一样的）

有

\[(cA(x))' = cA'(x) \\ (A(x) \pm B(x))' = A'(x) \pm B'(x) \\ (A(x)B(x))' = A(x)B'(x) + A'(x)B(x) \\ (\cfrac{1}{A(x)})' = -\cfrac{A'(x)}{A(x)^2} \\ (A(B(x)))' = A'(B(x)) B'(x) \]

这些是导数的基本法则。

有了多项式导数，我们可以逆推出原函数，但是会丢失常数项：

\[[x^i]A_x = [x^{i-1}]A'(x) / i(i \ge 1) \]

泰勒展开

常见的泰勒展开公式：

\[e^x = 1 + x + \cfrac{x^2}{2!} + ... = \sum \limits_{i \ge 0}\cfrac{x^i}{i!} \\ \ln(1-x) = -1 - x - \cfrac{x^2}{2} - ... = - \sum \limits_{i \ge 1}\cfrac{x^i}{i} \\ \ln(1+x) = x - \cfrac{x^2}{2} - ... = - \sum \limits_{i \ge 1}(-1)^{i-1} \cfrac{x^i}{i} \]

注意第三个公式中符号。

将给定的多项式和麦克劳林级数复合：

\[\ln(1 - A(x)) = - \sum \limits_{i \ge 1} \cfrac{A(x)^i}{i} \\ \exp(A(x)) = \sum \limits_{i \ge 0} \cfrac{A(x)^i}{i!} \]

求对数和指数

对数函数：
给定 \(A(x) = 1 + \sum \limits_{i \ge 1} a_i x^i\)。令 \(B(x) = \ln(A(x))\)。

那么因为对数函数的导数是 \(1/x\)，所以

\[\cfrac{\mathrm dB(x)}{\mathrm dA(x)} = \cfrac{1}{A(x)} \\ \mathrm dB(x) = \cfrac{\mathrm dA(x)}{A(x)} \]

两边同时除以 \(\mathrm dx\) 得到

\[B'(x) = \cfrac{A'(x)}{A(x)} \]

需要求出 \(A(x)\) 的乘法逆元。时间复杂度 \(O(n \log n)\)。

指数函数：

类似地有

\[B'(x) = B(x) A'(x) \]

比较系数得（别忘记 exp 和 ln 也是对多项式在数值上成立）

\[b_0 = 1 \\ b_i = \cfrac{1}{i} \sum \limits_{1 \le k \le i} ka_kb_{i-k} (i \ge 1) \]

第二个式子可以比较容易推导得到：

\[\begin{array} \left [x^i]B'(x) = (i + 1) B_{i + 1} \\ ~~~~~~~~~~~~~~= \sum \limits_{a + b = i} [x^a]B(x)[x^b]A'(x) \\ ~~~~~~~~~~~~~~= \sum \limits_{a + b = i + 1} B_a b A_b \end{array} \]

使用分治 FFT，做到 \(O(n \log^2 n)\)，如果用 \(\ln\) 求 \(\exp\) 牛顿迭代是 \(O(n \log n)\) 的。