连通分量

tarjan 算法对无向图连通性的应用：

• 求割点 -> 点双连通分量 -> 缩点建圆方树
• 求割边 -> 边双连通分量 -> 缩点建树

tarjan 算法对有向图连通性的应用：

• 求强连通分量，但是 kosaraju 比较自然。

主要思想

无向图的 dfs 树里面不会出现横叉边。容易证明。于是只有返祖边会形成环。环是双连通分量出现的基础。

考虑一个子树去除了其根节点的部分叫做“余子树”（也就是所有儿子的子树构成的集合），那么对于一个点，其子树的每一个节点都能经过非树边到达这个子树（根是自己）之外的其他节点，那么这个点连向其父亲的边就不是割边。如果对于一个点，其余子树都能经过非树边到达这个子树（根是自己）之外，那么这个节点就不是割点。

一个子树 dfn 连续。因此某一个子树的 dfn 的范围是 \([dfn_{root}, ?]\)。因此子树之外的 dfn 范围是 \([1, dfn_{root}) \cup (?, +\inf]\)，余子树之外的 dfn 范围是 \([1, dfn_{root}] \cup (?_{son}, +\inf]\)。

因此考虑对于一个点，记录其能绕（指不经过树边）到的最小 dfn 是多少（为什么是最小，因为试图跳出子树之外；并且只要有返祖边，那么连到的位置一定比自己小，所以不用考虑比自己大的 \(dfn\)。），这个叫 \(low\)。然后沿着树边上传，因为每一个节点影响范围都是它的所有祖先。

因此对于一个节点的子树，更新 low。否则更新 dfn，就一目了然了。

无向图 k-连通分量

途径：一个点和边的交错序列 \(w = [v_0, e_1, v_1, ..., e_k, v_k]\)。

回路和圈（环）：是特殊的途径，满足 \(v_0 = v_k\)，并且回路指除了首尾不经过同一条边的途径；圈（环）指除了首尾不经过同一个点的途径（圈包含回路）对于途径上点和边的导出子图，回路也叫欧拉回路，圈也叫哈密顿回路。本文里为了方便统一使用欧拉回路和哈密顿回路的叫法，但是原文用的是回路和圈。

迹和路径：迹是保证没有两个 \(e\) 相同的途径，也叫欧拉路。路径是不保证 \(v_0 = v_k\)，但是保证除了首尾不经过同一个点的途径。也叫哈密顿路。为了方便后文也只使用欧拉路和哈密顿路这两种叫法。

k-连通：\((i,j)\) k-点/边连通的意思是，\((i, j)\) 之间可以有 \(k\) 条不交的哈密顿路连接，这些路径都不经过同一个点/边。

Menger 定理：\((i,j)\) k-点/边连通，可以看做在无向图中跑 \(i \rightarrow j\) 的，点流量/边流量限制为 \(1\) 的最大流 \(\ge k\)。也即，不存在大小 \(< k\) 的点/边割集使得 \(i, j\) 分开。

等价关系：在某集合 \(S\) 中定义的二元关系集合 \(T = \{(i, j) | i \in S, j \in S\}\)，满足自反性（\((i, i) \in T\)）无向性（\((i, j) \in T \rightarrow (j, i) \in T)\)）和传递性 （\((i, j) \in T, (j, k) \in T \rightarrow (i, k) \in T\)），那么称这个关系是等价关系，集合 \(S\) 可以根据这个关系划分成若干个中间没有边的团。

k-边连通分量对点是等价关系。
证明：对于 \((i, j), (j, k)\) 满足其 k-边连通，考虑 \((i,k)\) 的边割集，\(j\) 包含于 \(i\) 或者 \(k\) 集合，那么其也是 \((i, j)\) 或 \((j, k)\) 的边割集。矛盾。因此原命题成立。

边双连通分量：2-边连通分量。
点双连通分量：2-点连通分量，但是对 \(K_2\) 的点连通度定义不同，定义为 \(2\)，也就是说，\(K_2\) 认为是一个点双连通分量。

双连通分量的特殊性质：如果两个点在同一个边/点双连通分量上，那么这两个点属于同一条欧拉回路/哈密顿回路。于是，这条欧拉回路/哈密顿回路上所有点均双连通（边双不过同一边，点双不过同一点）。所以，双连通分量一定是一个连通块，而 k \(\ge 3\) 的时候不一定，例如：

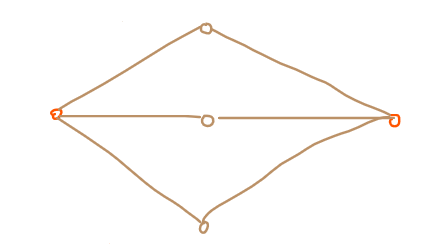
黄色的点是一个 3-点连通分量。

这个性质让我联想到哈密顿回路，\(n \ge 3\) 的哈密顿回路是所有点属于同一个环，所以如果一张 \(n \ge 3\) 的图不是一个点双的话，一定没有哈密顿回路。

点双连通分量对边是等价关系。
考虑 \(e_1, e_2\) 在一个点双中，\(e_3, e_2\) 在一个点双中，那么 \(e_1, e_3\) 也在一个点双中。
\(e_1, e_2\) 在一个点双中，当且仅当他们在同一个哈密顿回路中。但是一个点双不一定有哈密顿回路，因为可以是若干个哈密顿回路的嵌套：

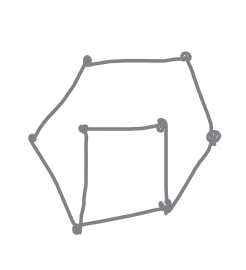
求点双和边双：

打上 //1, //2 ... 是需要注意的地方。
注意两个前提分别是 \(low_v = v\), \(low_u \ge v\)，第二个尤其要注意，有桥边的存在。

然后点双弹栈只能弹到 \(u\)，而不是 \(v\)，这个一定要注意。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr  << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
    string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; } 
    reverse(s.begin(), s.end()); cerr << s << endl; 
    return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍！
//use std::array.
int to[4000020], dfn[500050], low[500050]; int cnt = 0; int ecnt = 0;
vector<int> t[500050];
vector<vector<int>> dcc;
stack<int> stk;
void dfs(int x, int k) {
    stk.push(x);
    dfn[x] = low[x] = ++cnt; //1
    for(int i : t[x]) {
        if(i == (k ^ 1)) continue;
        else if(!dfn[to[i]]) {
            dfs(to[i], i); //2
            cmin(low[x], low[to[i]]);
        }
        else {
            cmin(low[x], dfn[to[i]]);
        }
    }
    if(low[x] == dfn[x]) {
        vector<int> v;
        while(!(stk.top() == x)) {
            v.push_back(stk.top());
            stk.pop();
        }
        v.push_back(stk.top());
        stk.pop();
        dcc.push_back(v);
    }
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    //freopen();
    //freopen();
    //time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    int n, m; cin >> n >> m;
    f(i, 1, m) {
        int u, v; cin >> u >> v;
        to[ecnt] = v; t[u].push_back(ecnt++);
        to[ecnt] = u; t[v].push_back(ecnt++); //4
    }
    f(i, 1, n) if(dfn[i] == 0) dfs(i, -1); //3
    cout << dcc.size() << endl;
    for(vector<int> v : dcc) {
        cout << v.size() << " ";
        for(int i : v) {
            cout << i << " ";
        }
        cout << endl;
    }
    //time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}
/*
2023/x/xx
start thinking at h:mm


start coding at h:mm
finish debugging at h:mm
*/

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr  << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
    string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; } 
    reverse(s.begin(), s.end()); cerr << s << endl; 
    return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍！
//use std::array.
vector<int> g[500500];
vector<vector<int>> dcc;
int dfn[500500], low[500500]; int dcnt = 0;
stack<int> stk;
void dfs(int x, int k) {
    stk.push(x);
    dfn[x] = low[x] = ++dcnt;
    for(int i : g[x]) {
        if(i == k) continue;
        else if(!dfn[i]) {
            dfs(i, x);
            cmin(low[x], low[i]);
            if(low[i] >= dfn[x]) {
                vector<int> v;
                while(stk.top() != i) {
                    v.push_back(stk.top());
                    stk.pop();
                }
                v.push_back(i); //2
                stk.pop();
                v.push_back(x);
                dcc.push_back(v);
            }       
        }
        else {
            cmin(low[x], dfn[i]);
        }
    }
    // cout << x << " " << dfn[x] << " " << low[x] << endl;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    //freopen();
    //freopen();
    //time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    int n, m; cin >> n >> m;
    f(i, 1, m) {
        int u, v; cin >> u >> v;
        if(u == v) continue;
        g[u].push_back(v); g[v].push_back(u);
    }
    f(i, 1, n) {
        if(g[i].empty()) {dcc.push_back({i});}
        else if(!dfn[i]) dfs(i, 0);
    }
    cout << dcc.size() << endl;
    for(vector<int> v : dcc) {
        cout << v.size() << " ";
        for(int i : v) {
            cout << i << " ";
        }
        cout << endl;
    }
    //time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}
/*
2023/x/xx
start thinking at h:mm


start coding at h:mm
finish debugging at h:mm
*/

关于圆方树：

两个点双的点交集至多为 \(1\)。所以我们把每一个点双建成虚点，把每一个在点双上的点向点双连边，得到的就是一棵树。没有那么复杂的建立，只是连边即可。

省选联考 2023 D1T2

【题意】
在这个国度里面有 \(n\) 座城市，一开始城市之间修有若干条双向道路，导致这些城市形成了 \(t≥2\) 个连通块，特别的，这些连通块之间两两大小差的绝对值不超过 \(0≤k≤1\)。为了方便城市建设与发展，\(n\) 座城市中的某 \(t\) 座城市在这 \(t\) 座城市之间额外修建了至少一条双向道路，使得所有城市连通。

现在已经知道额外修建后的所有道路，你需要算出有哪些双向道路集合 \(E′\)，满足这些道路有可能是后来额外修建的，请输出答案对 \(998,244,353\) 取模的结果。
【分析】
主要讲讲学到了什么。

首先无向图图论题目，连通性问题就是想到 dfs 树上，基本没有其他做法了。可以发现，某一个块是 dfs 树上的一个连通块。

然后你可以想一下树，但是对于这样的树形 dp，一定要搞清楚。我们是要把树划分为若干个部分，其中每个部分大小差别最大 \(1\)。而且两个部分之间的连边组成了一棵树。注意到如果钦定一个根，那么每一个块之间交接的点都有若干个儿子属于自己这一块，若干个儿子是别的块的根。考虑树形 dp 根。这里可以考虑先按照 size sort 一下子树，然后有两个讨论，所以一定要先写在纸上写清楚了然后再开始写。

然后考虑扩展到图。我们需要发现另一个性质：对于一个点双（这里要考虑一下是 2-点（如果 2-点，那么求出来点双特判一下大小为 2，然后直接对两个孤立点连边，注意这时候圆圆之间有连边，是割边） 还是 点双，但是这题是一样的），要么每个点都属于不同的块，要么都属于同一个块。然后建圆方树之后，需要把它切开，每一块有 \(x\) 个圆点。注意分类，这两种点分别怎么切：

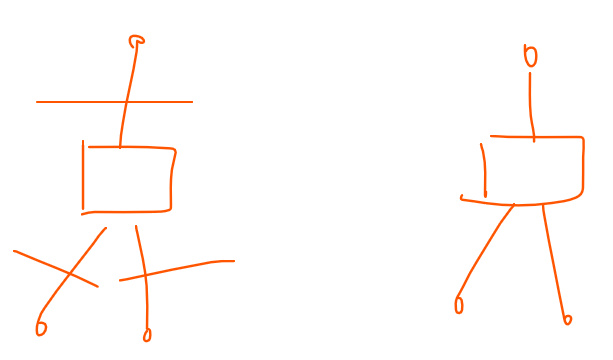
不难定义方点的 dp 值为其所有儿子 dp 值的乘积，这是因为如果这么定义，第一种切割方式会算进父亲的 dp 里，第二种 dp 值没有用。

然后就可以树上 dp 了。

主要的两点是考虑到性质高度挂钩于圆方树，还有写好树形 dp。

强连通分量

Kosaraju 算法：
该算法依靠两次简单的 DFS 实现：

第一次 DFS，选取任意顶点作为起点，遍历所有未访问过的顶点，并在回溯之前给顶点编号，也就是后序遍历。

第二次 DFS，对于反向后的图，以标号最大的顶点作为起点开始 DFS。这样遍历到的顶点集合就是一个强连通分量。对于所有未访问过的结点，选取标号最大的，重复上述过程。

两次 DFS 结束后，强连通分量就找出来了，Kosaraju 算法的时间复杂度为 \(O(n+m)\)。

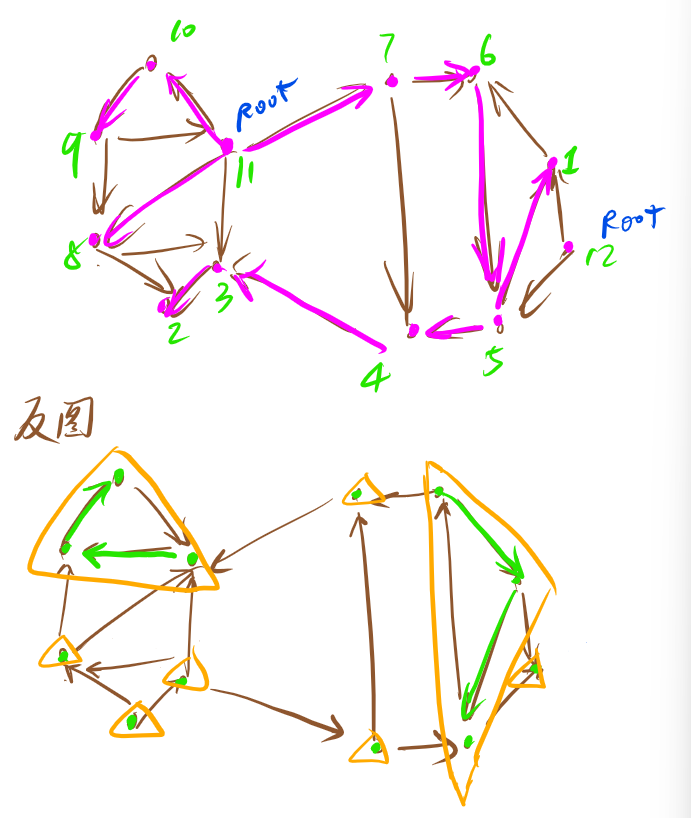
这个算法的思想是很直接的，就是考虑一个强连通分量是一个非简单环，而环的反图还是环，但非环的反图不是环。正反走两遍都能到的话，说明就是一个环。

对于标号，其标记的是 scc 缩点后的拓扑序（tarjan 标记的是反拓扑序）。