线性空间
参考资料:
《线性代数》第三章
https://www.acwing.com/video/2274/
《进阶指南》
update 2023.2.3: 优化板子。
定义
-
称 \((a_1,a_2,...,a_k)\) 为 \(k\) 维向量 \(\bold{a}\),其中 \(a_i \in \R\) 称为 \(k\) 维实向量。每个维度之间没有关系。
-
若干个同维数向量的组合称为向量组。向量组可以是无限的。
-
向量的线性运算包括数乘和加减运算,具有所有运算律。
-
若存在向量 \(\bold{b}\) 可以由向量组 \(\bold{a_1,a_2,...}\) 通过线性运算表示出来,则称 \(\bold{b}\) 能被 \(\bold{a}\) 线性表出。
-
对于向量组 \(\bold{a_1,a_2,...}\),所有能被它表出的向量构成一个向量线性空间,它称为 \(\bold{a_1,a_2,...}\) 的子空间。\(\bold{a_1,a_2,...}\) 称为该空间的生成子集。
-
若向量组 \(\bold{a_1,a_2,...}\) 中任意元素都可以被向量组 \(\bold{b_1,b_2,...}\) 表出,那么显然向量组 \(\bold{b_1,b_2,...}\) 中任何元素也可以被向量组 \(\bold{a_1,a_2,...}\) 表出。称它们等价。
-
若向量组 \(\bold{a_1,a_2,...}\) 满足对于非全零的 \(k_1,k_2,...\) 使得 \(\sum \bold{a_i} k_i = \bold{0}\) 成立,那么称 \(\bold{a_1,a_2,...}\) 线性相关。否则称 \(\bold{a_1,a_2,...}\) 线性无关。
- 与之等价的定义:对于任意的 \(i\),有 \(\bold{a_i}\) 可以被向量组 \(\bold{a_1,a_2,...}\) 中其他的向量构成的向量组表出,则称 \(\bold{a_1,a_2,...}\) 线性相关。否则,一定不存在 \(i\) 满足该结论,称 \(\bold{a_1,a_2,...}\) 线性无关。
-
一个向量组 \(\bold{a}\) 的极大线性无关组的定义:从 \(\bold{a}\) 中可以找到若干个向量组成新的向量组 \(\bold{a'}\),并且 \(\bold{a'}\) 满足:
- 其线性无关。
- 将任何一个除 \(\bold{a'}\) 中元素之外的向量加入该组,该组均变得线性相关。
-
向量组 \(a_1 = \{1,...,0\}, a_2 = \{0,1,...,0\},...\}\) 线性无关。
证明:考虑构造非全零的 \(k_1,k_2,...\) 使得 \(\sum \bold{a_i} k_i = \bold{0}\) 成立。那么我们将向量组看成一个按行分块的矩阵,其系数为 \(k_i\),右边加上一堆零生成的增广矩阵也就是原线性方程组。那么进行任意次矩阵的线性变换之后,该矩阵表示的向量组均与原向量组等价。- 因此对于该分块矩阵,解出唯一解为 \(k_1=k_2=...=0\),因此不成立。故原向量组线性无关。
-
对于向量组,我们可以对其生成的按行分块的矩阵进行高斯消元化成简化阶梯形矩阵后,留下的所有非零向量构成的向量组都为原方程组的极大线性无关组。
- 证明:反证。如若不然,则第一个元素可以被后面其他的该行元素线性表出。(注意维度之间没有关系,若干个向量加起来是 \(\bold{0}\),也就是说这些向量每一个维度的和都是 \(0\),这点由零向量的定义 \(\bold{0} = (0,0,...,0)\) 得出。)
注意高斯消元针对的是向量构成的行矩阵本身,而非求解线性方程组。得出来的分块矩阵就是高斯消元之后的结果,是一个极大线性无关组。而证明它是极大线性无关组才需要利用到方程。
- 证明:反证。如若不然,则第一个元素可以被后面其他的该行元素线性表出。(注意维度之间没有关系,若干个向量加起来是 \(\bold{0}\),也就是说这些向量每一个维度的和都是 \(0\),这点由零向量的定义 \(\bold{0} = (0,0,...,0)\) 得出。)
-
一个向量组的极大线性无关组不唯一,但其内元素个数都相等。也即,一个线性空间的基底的元素个数固定。
- 高斯消元过程中无论如何切换元素,自由元的个数是一样的,也就是说非零行的个数一样,也就是极大线性无关组内个数一样。
- 这个个数称作这个向量组的秩(rank),记作 \(R(\bold{a_i,a_2,...})\)。
-
向量组 \(\bold{a_i,a_2,...}\) 线性无关的充要条件是 \(R(\bold{a_i,a_2,...,a_m}) = m\)。对于一个线性相关组,其秩为 \(m\),那么从中挑选任意 \(m+1\) 个向量构成的组都线性相关。
-
异或空间上的一些数能够表出的数的个数是 \(2^m\)。(如果不承认空集表出 \(0\),那么可能是 \(2^m\) 或者 \(2^m - 1\)。)
应用
例如给定 \(10^5\) 个向量的 \(60\) 维向量组,那么它的生成子空间的基底包含的向量数量 \(\le 60\)。因此可以极大地简化向量组的所含信息。并且此时对分块矩阵高斯消元的时间复杂度为 \(O(10^5 \times 60 \times 60)\),也就是 \(O(nm^2)\)。
我们可以类似地定义异或空间。若 \(b\) 可以被 \(a_1,a_2,...,a_n\) 经过异或运算表出,那么 \(b\) 在 \(\{a\}\) 的生成子空间里。我们把每个数拆成二进制之后相当于一个 \(k\) 维向量,维数等于 \(\log{a_i}\)。这也就是我们 OI 里通常所说的“线性基”。在高斯消元的排序和消除步骤中,由于可以对整个数进行操作,相当于压位操作,可以优化一个 \(m\),那么时间复杂度为 \(O(nm)\)。
acwing 3164
题意:给定 \(n\) 个整数,需要从中挑选任意个整数,使得异或和最大。
分析:建立完线性基之后,得到的矩阵形如下图:
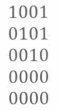
重要性质:从前到后,线性基的某一位的最高非零位为第 \(j\) 位的话,之后所有位置的第 \(j\) 位均为 \(0\)。
因此从前到后贪心。维护答案 \(ans\),若枚举到了第 \(i\) 个数,其最高非零位为 \(j\),那么如果 \(ans\) 的第 \(j\) 位为 \(0\),那么选择这个数异或上 \(ans\),使其第 \(j\) 位变成 \(1\),一定更优。否则不选择。为了代码简便,可以比较 \(ans \oplus a[i]\) 与 \(ans\) 的大小。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {
if(x < y) x = y;
}
void cmin(int &x, int y) {
if(x > y) x = y;
}
int a[100010];
int ans;
int m=63;
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n;
cin >> n;
f(i,1,n)cin>>a[i];
int h=1,l=m;
int ans =0;
for( ; l>=0; l--) {
//找非零元素
f(i,h,n) if((a[i] >> l)&1) {
swap(a[h],a[i]);
break;
}
if(!((a[h]>>l)&1)) continue;
f(i,h+1,n)if((a[i]>>l)&1)a[i]^=a[h];
if((ans^a[h])>ans) ans^=a[h];
h++;
}
cout << ans << endl;
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
acwing210
求第 \(k\) 小的能异或出的值。
分析:
线性基中任何数不会被其他数表出,那么如果取数的方案不同,那么一定会生成不一样的数。并且走到第 \(i\) 位的时候,不管选了什么,选第 \(i\) 个的方案一定比不选的方案优(或者劣),方案不重复。那么可以走到下一位,并查询对应的 \(rank\)。
ans 每次询问都要清空。多测时没清空的 a_i 会对 a_c 的判断造成影响,这个要注意!
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
int a[100010];
int m = 63;
int r, c;
int pow2[65];
int ans = 0;
void find(int now, int rnk) {
if(now == c)return;
int mid=pow2[c-1-now];
if(rnk > mid) {
if((a[now] ^ ans) > ans) ans ^= a[now];
find(now + 1, rnk-mid);
}
else {
if((a[now] ^ ans) < ans) ans ^= a[now];
find(now + 1, rnk);
}
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int T; cin >> T;
pow2[0]=1;
f(i,1,m)pow2[i]=pow2[i-1]*2;
int cnt=0;
while(T--) {
ans=0;
cout<<"Case #"<<++cnt<<": \n";
int n; cin >> n;
f(i, 1, n) cin >> a[i];
r=m,c=1;
for(;r>=0;r--){
f(i,c,n)if((a[i]>>r)&1){
swap(a[i],a[c]);break;
}
if(c>n||!((a[c]>>r)&1)) continue;
f(i,c+1,n)if((a[i]>>r)&1)a[i]^=a[c];
c++;
}
int q; cin >> q;
f(i,1,q){
ans=0;
int x;cin>>x;
if(c-1 == n)x++;
if(x>pow2[c-1])cout<<-1<<endl;
else {find(1,x);cout<<ans<<endl;}
}
}
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
更好的写法
有另外一种构造方式,可以实现每次动态插入数的过程。不仅动态,而且好写非常多。
这种线性基,第 \(i\) 个数的最高位就是第 \(i\) 位,或者不存在这个数。
插入过程是:从大到小枚举位数,目标是使得剩下插入的这个数没有办法被其他数表出,那么如果该位已经有数字了,那么直接异或掉。
void insert(bas &x, int k) {
for(int j = 31; j >= 0; j --) {
if((k >> j)) {
if(x.b[j] == 0) {
x.b[j] = k;
break;
}
k ^= x.b[j];
}
}
}
时间复杂度不会变。
以后都要这样写。
线性基可以合并,像摩尔投票一样,可以封装起来用线段树维护它。线性基合并的时间复杂度是 \(O(|base_1||base_2|)\),通常是两个 \(\log\) 级别。
CF587E
【题意】
给定一个序列,有两个操作:
- 区间异或某个数
- 查询区间内的数能够异或表达出的数的个数,包括空集 \(0\)。
\(n \le 2 \times 10^5, q \le 4 \times 10^4\)
【分析】
我们考虑线段树维护,最难做的是信息和标记合并。也就是某区间异或上某个数后,线性基的变化。需做到 \(\mathrm{polylog}\)。
我们考虑异或空间里的数,如果奇数个数能够组成 \(x\),那么改变之后能够组成 \(x \oplus d\),如果偶数个数能够组成 \(x\),那么改变之后能够组成 \(x\)。
对于异或空间里的数,同时被奇数和偶数个数组成的数存在(一旦存在就所有数都是)当且仅当存在奇数个数表示出 \(0\)。
于是我们线性基里面额外维护是否能够奇数个数表出 \(0\),并且维护每一个元素被几个原数组里的数表示出来即可。
做异或的时候,分奇偶讨论,最多分出 \(2 \log\) 个数。
(注意合并的时候重新分配奇偶,而原来的奇数个数表出 \(0\) 在异或之后不起作用,重新算)
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
const int bit = 31; int pow2[40]; int a[200010]; int n, q;
struct lbs {
pii b[32]; bool d; //b: [奇数还是偶数个数能够表示, 数]:如果第二个数是0,第一个数未定义。
lbs() {f(i, 0, bit) {b[i] = {0, 0};} d = 0; } //d:是否能够通过奇数个数表出0.
int cnt() {
int res = 0;
f(i, 0, bit) if(b[i].second != 0) res ++;
return res;
}
void insert(pii x) {
for(int i = bit; i >= 0; i --){
if((x.second >> i) & 1) {
if(b[i].second != 0) {
x.second ^= b[i].second;
x.first ^= b[i].first;
}
else {
b[i] = x; return;
}
}
}
if(x.first == 1) d = 1;
}
void change(int op) {
if(op == 0) return;
// cerr << "change : " << op << endl;
pii c[64] = {{0, 0}};
if(d == 1) {
f(i, 0, 31) c[i] = {0, b[i].second};
f(i, 32, 63) c[i] = {1, b[i - 32].second ^ op};
}
else {
f(i, 0, 31) {
if(b[i].first == 0) {c[i] = b[i];}
else {c[i] = {b[i].first, b[i].second ^ op};}
}
}
bool td = 0;
// cerr << "c: "<<endl;
// f(i, 0, bit + 1) if(c[i] != 0) pofe(c[i],bit);
f(i, 0, bit) b[i] = {0, 0};
f(x, 0, 2 * bit + 1) {
for(int i = bit; i >= 0; i --){
if((c[x].second >> i) & 1) {
if(b[i].second != 0) {
c[x].second ^= b[i].second;
c[x].first ^= b[i].first;
}
else {
b[i] = c[x]; break;
}
}
if(i == 0) {
if(c[x].first == 1) td = 1;
}
}
}
// assert(d == 0 || td == 1);
d = td;
}
lbs merge(lbs op) {
lbs t = *this; t.d = d | op.d;
for(int i = bit; i >= 0; i --) {
if(op.b[i].second != 0) t.insert(op.b[i]);
}
return t;
}
// void bl() {
// for(int i = 0; i <= bit; i ++) {
// if(b[i].second != 0) {cerr << b[i].first << ", ";
// pofe(b[i].second, bit);
// }
// }
// }
};
struct sgt {
lbs xxj[1000010];
int tag[1000010];
void pushdown(int now) {
xxj[now * 2].change(tag[now]);
xxj[now * 2 + 1].change(tag[now]);
tag[now * 2] ^= tag[now];
tag[now * 2 + 1] ^= tag[now];
tag[now] = 0;
}
void add(int now, int l, int r, int x, int y, int k) {
if(l >= x && r <= y) {
xxj[now].change(k); tag[now] ^= k;
return;
}
if(l > y || r < x) return;
int mid = (l + r) >> 1; pushdown(now);
add(now * 2, l, mid, x, y, k);
add(now * 2 + 1, mid + 1, r, x, y, k);
xxj[now] = xxj[now * 2].merge(xxj[now * 2 + 1]);
return;
}
lbs query(int now, int l, int r, int x, int y) {
if(l >= x && r <= y) return xxj[now];
if(l > y || r < x) return lbs();
int mid = (l + r) >> 1; pushdown(now);
return query(now * 2, l, mid, x, y).merge(query(now * 2 + 1, mid + 1, r, x, y));
}
int ask(int l, int r) {
lbs tt = query(1, 1, n, l, r);
// cerr << "query result: the inside is: " << endl;
// tt.bl();
return pow2[tt.cnt()];
}
void build(int now, int l, int r) {
xxj[now] = lbs();
if(l == r) {
// cerr << "insertion: " << 1 << " " << l << " " << a[l] << endl;
xxj[now].insert({1, a[l]});
// cerr << "can odd 0 ? " << xxj[now].d << endl;
return;
}
int mid = (l + r) >> 1;
build(now * 2, l, mid); build(now * 2 + 1, mid + 1, r);
xxj[now] = xxj[now * 2].merge(xxj[now * 2 + 1]);
}
// void dfs(int now, int l, int r) {
//
// cerr << "node [" << now << "], range from [" << l << ", " << r << "], size = " << xxj[now].cnt() << endl;
// cerr << "can / can't get 0 with odd numbers: " << xxj[now].d << endl;
//cerr << "the inside is: " << endl;
//xxj[now].bl();
// if(l == r) return;
// dfs(now * 2, l, (l + r) / 2);
// dfs(now * 2 + 1, (l + r) / 2 + 1, r);
// }
}xds;
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
pow2[0] = 1; f(i, 1, bit) pow2[i] = pow2[i - 1] * 2;
cin >> n >> q;
f(i, 1, n) cin >> a[i];
xds.build(1, 1, n);
f(i, 1, q) {
int op; cin >> op;
if(op == 1) {
int l, r, k; cin >> l >> r >> k; xds.add(1, 1, n, l, r, k);
}
else {
int l, r; cin >> l >> r; cout << xds.ask(l, r) << endl;
}
//xds.dfs(1, 1, n); cerr << endl;
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at h:mm
start coding at h:mm
finish debugging at h:mm
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号