高斯消元

普通高斯消元

高斯消元是求解线性方程组的方法。对于一个 \(m\) 个等式 \(n\) 个未知数的方程组，我们可以将其写成 \(m \times (n + 1)\) 的增广矩阵的形式：

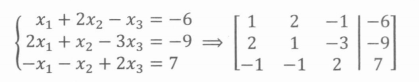
对于这个矩阵我们可以进行三种“初等行变换”操作：

• 对一行内的所有元素乘以一个非零实数 \(k\)。（乘以 \(0\) 也成立，但是没有意义，算不出解）
• 交换两行的元素。
• 把其中一行的若干倍加到另一行上。

做完之后矩阵依旧正确。（对于行列式也是这三种，但是它们对行列式的数值分别有不同的影响。）

我们考虑通过将增广矩阵运用初等行变换操作的方式解出所有解。

具体步骤如下：

• 遍历还没有处理的第 \(i\) 行。
  • 考虑目前需要消掉第 \(j\) 个元，也就是目标是让处理之后 \(i+1 \sim m\) 行里面第 \(j\) 个元的系数都是 \(0\)。
  • 先找到一个非零元素作为主元，将其所在的一行与第 \(i\) 行交换。如果有精度问题，那么当这个非零元素的绝对值为最大时（对于有模数或者无论如何进行初等行变换都是整数矩阵的时候不需要；但是你很容易发现如果用小的，那么会出现问题，所以你记不住的话大小都试试！），期望精度最好（因为如果用最小的，那么减掉的时候要减掉 $ k \times a_i$，这个 \(k\) 很大，这时候乘法精度很不好）。利用 fabs(x) 函数计算浮点数 \(x\) 的绝对值。如果不存在非零元素，那么已经处理好第 \(j\) 个元，此时在不增加 \(i\) 的情况下处理第 \(j+1\) 个元。
  • 将第 \(i\) 行（也就是主元所在的一行）的第 \(j\) 个系数变为 \(1\)，也就是整行除以这个系数。（这对 double 的精度很有帮助）
  • 对于第 \(i+1 \sim m\) 行，每行减去该行内 \(j\) 的系数乘以第 \(i\) 行。
  • 如此，这些行都满足了要求。
• 如此，矩阵变成了一个上三角矩阵。如下图所示。
  
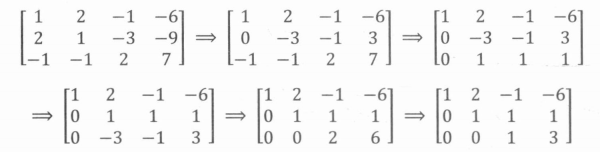
• 现在要从底部一一代入已经求解好的值，从而把矩阵变成一个对角矩阵：
  
• 考虑解的个数。
  • 如果是上图的矩阵格式，那么有唯一解，也就是 \(x_1 = 1, x_2 = -2, x_3= 3\)。
  • 否则考虑零行。（也就是系数均为 \(0\) 的一行）。如果存在常数不为 \(0\) 的零行，那么无解。如果不是无解，那么自由元的个数就是总元的个数减去非零行的个数。
    例如下图，当 \(x_1\) 确定为任何值的时候，都有一个 \(x_2\) 可以使得满足条件。也就是说存在一个自由元。（也就是一个非零行锁定一个元）
    
    

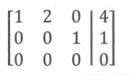
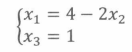
对于 \(n\) 个等式 \(m\) 个元组成的矩阵，时间复杂度为 \(O(nm\min(n,m))\)。（jiangly 的指正，因为如果有主元的元素才会执行 \(O(nm)\) 的算法，其他情况直接退出了。）

书写高斯消元的时候强烈建议先在纸上列一遍伪代码。（4.27，没有写伪代码但是一遍敲对了。）

---

代码实现：

其中 b[n][n + 1] 是增广矩阵，其中第 n+1 列是常数。
这里保证一定有唯一解。
（source：acwing 207）

void gauss() {
    //消成上三角矩阵
    f(i, 1, n) {
        //枚举把哪一列的元素求出，也就是哪一行换成上三角形式
        //找绝对值最大的元素作为非零元素（可以提升精度）
        int maxj = 0;
        f(j, i, n) if(fabs(b[j][i]) > fabs(b[maxj][i])) maxj = j;
        //交换
        f(j, i, n + 1) swap(b[i][j], b[maxj][j]);
        //归一，因为要用到最初的元素，所以倒着处理，下同
        for(int j = n + 1; j >= i; j--) b[i][j] /= b[i][i];
        //相减
        f(j, i + 1, n) for(int k = n + 1; k >= i; k--) b[j][k] -= b[i][k] * b[j][i]; 
    }
    //消成对角矩阵
    for(int i = n; i >= 1; i--) {
        f(j, 1, i - 1) {
            b[j][n + 1] -= b[j][i] * b[i][n + 1];
            b[j][i] = 0;
        }
    }
}

不保证唯一解。此时消去哪一行要和计算哪一个元的标号区分开。

（source：acwing 208）

void out() {
    //调试技巧，写成函数
    f(i, 1, n) f(j, 1, n + 1) cout << b[i][j] << " \n"[j == n + 1]; 
}
int gauss() {
    int h, l;
    for(h = 1, l = 1; l <= n; l++) {
        //h: 现在消哪一行。l: 现在消哪一个x。
        //异或，整数解，不关心精度问题
        //只需要找到第一个非零元素即可作为主元。
        int zy = 0;
        f(j, h, n) if(b[j][l]) {zy = j; break;}
        //没有非零元素就退出
        if(zy == 0) continue;
        
        //交换
        f(j, l, n + 1) swap(b[zy][j], b[h][j]); 
        //不用归一，因为一定是一
        //相减
        f(j, h + 1, n) for(int k = n + 1; k >= l; k--) {
            b[j][k] -= b[j][l] * b[h][k];
        } 
        h++;
    }
    //算答案，答案为 2 * 自由元个数，也就是 2 * 零行个数
    int ans = 1;
    if(h <= n) {
        f(i, h, n) {
            if(b[h][n + 1]) return -1;  //0 = !0, 无解
            else ans *= 2;  //多一个自由元
        } 
    }
    return ans;
}

ABC276Ex

灯泡题的化用。

一些特化的高斯消元

树上高斯消元

考虑这样一个方程组的高斯消元：有一棵树，每一个点所代表的方程式只包含其父亲，其自己，以及其儿子，特别地，根节点的式子只和其自己，以及其儿子有关；叶子节点的式子只和其父亲有关。这样的方程式可能由树形期望 dp 导出：

\[dp_i = a dp_{fa_i} + \sum \limits_{i \rightarrow j} b_j dp_{j} \]

这样的式子，可以做到线性高斯消元：
考虑某一个点能不能变式为 \(dp_i = a dp_{fa_i} + c\) 的形式。稍微思考发现是可以的：我们考虑遍历所有儿子，假设所有儿子都已经转化为了这个形式，那么将 \(a\) 移项到左边，然后 \(b\) 放进 \(c\) 即可。

发现这样进行下去之后，最后根节点会变成 \(dp_{root} = c\) 的形式，然后再往下代进去即可。

带状矩阵高斯消元

带状矩阵：只有一个特定区域有可能非 \(0\) 系数的矩阵，如下图：

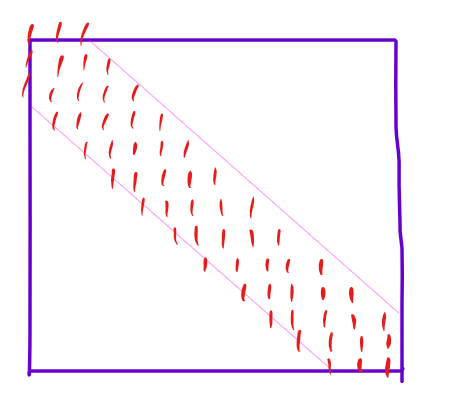
那么某一行往下只有 \(d\) 个位置需要消除，往右只有 \(d\) 个位置可能非 \(0\) 需要消除。如果一切正常那么时间复杂度是 \(O(nd^2)\)。

考虑如果遇到需要交换行的情况怎么办，也就是某一行没有主元，和其他行换一下的情况。

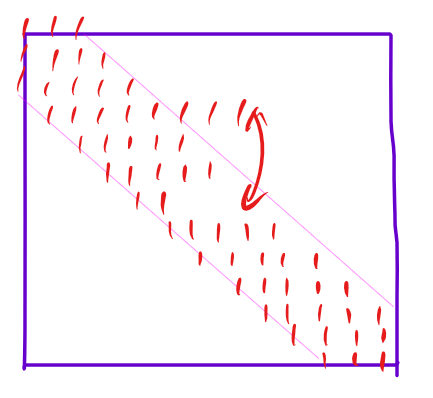
你会发现，这种情况下可能会破坏右边只有 \(d\) 个位置可以删除的性质。首先寻找主元的时候你依然只需要往下走 \(d\) 步，然后虽然破坏了性质但是依然往右只有 \(2d\) 个位置可能需要消除。

所以只需要每次往外找 \(2d\) 个即可，时间复杂度还是 \(O(nd^2)\)，常数为 \(2\)。

考虑最后还原的时候。你依然只需要向上找 \(2d\) 个数尝试代入。

如果右上角不保证不是 \(0\) 呢？那么你发现右边有 \(d\) 个数的性质没有了，但是下面只有 \(d\) 行的性质还在。因此可以 \(O(n^2d)\) 进行整个过程。

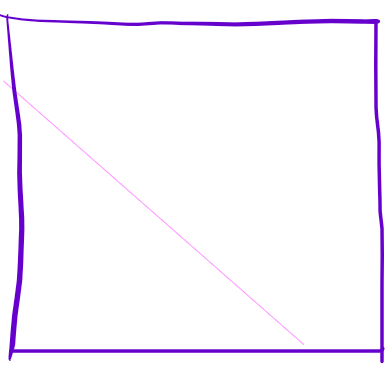
做前缀和

对于其他一些特异的矩阵，你也可以尝试找方法去优化高斯消元的过程。比如先对变量做一遍前缀和，体现在矩阵里面是对于每一行，系数做了一遍差分：

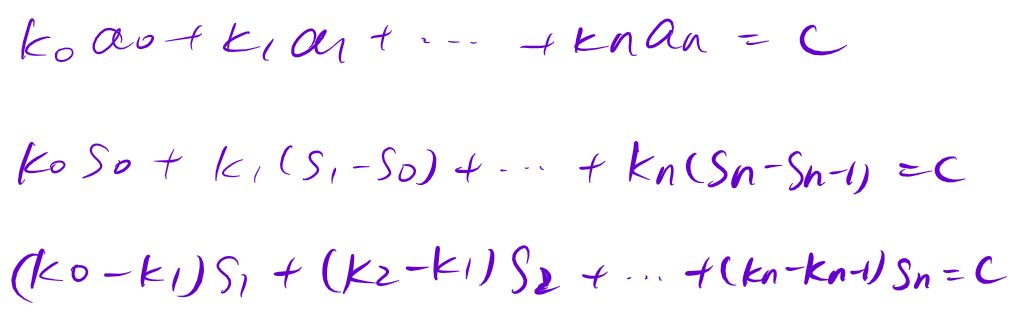
遇到一些比较平整的系数，可能会消成带状矩阵哦！