最短路图和最短路树

最短路图

对于点有点权的图 \(g= \{v,e\}\)，定义 \(i\) 到 \(j\) 的最短路径为所有 \(i\) 到 \(j\) 的路径中经过点权和。定义最短路图为 \(G=\{V,E\}\)，其中 \(V \subseteq v, E \subseteq e\)，并且 \(V\) 中的每条边都在至少一条 \(S \rightarrow T\) 的最短路上，\(E\) 中的每个点都在至少一条最短路上。

构建方案：考虑 \(dis\) 表示源点到该点的距离，\(sid\) 表示汇点到该点的距离，则 \(i -> j\) 存在于最短路图上当且仅当 \(dis[i] + sid[j] =\) 最短路距离。

这样构建出来的图是一个 DAG。在这个图上可以做一些事情。

Pjudge NOIP Round #3 Div.1B 抓内鬼

https://pjudge.ac/problem/21694

UR#24 的题面被内鬼偷走了！

为了找回丢失的题面，uoj 管理员决定和 pjudge 管理员合作，让内鬼无路可逃。

内鬼在一个 \(n\) 个点 \(m\) 条边的简单无向连通图上行走，他从 \(1\) 号点出发，目标是 \(n\) 号点。

uoj 和 pjudge 分别抓了 \(k\) 和 \(n−k\) 个壮丁。图上的每个点会恰好分配一个壮丁，负责盘问来往行人。因为人流量不同，一个人经过第 \(i\) 个点需要花费的时间是 \(t_i\) 。经过一条边的时间可以忽略不计。

uoj 的壮丁很清楚其他 uoj 的壮丁都是鸽子，pjudge 的壮丁也很清楚其他 pjudge 的壮丁都是鸽子，但他们相互不知道对方是不是鸽子。所以，只有当内鬼经过的一条边的两边的壮丁来自同一个 oj 时，他才会被抓住。

你需要构造一个分配壮丁的方案，使得对于任意一条 \(1\) 到 \(n\) 的最短路，内鬼走这条路都会被抓住。或者判断无解。

分析：

建出最短路图之后，按照拓扑排序，前 \(k\) 个给 U，其余的给 P 即可。

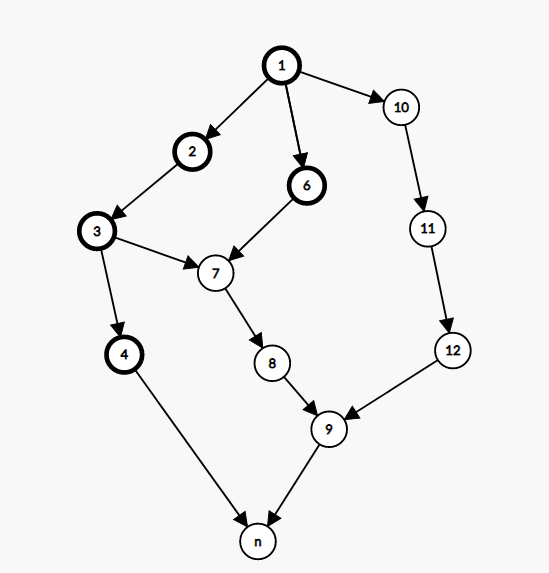
感性理解一下。只有最短路图是双层的，也就是 \(1,n\) 之间有连边并且 \(k=1\) 的时候这样才没有效果，这时我们要让 \(1\) 和 \(n\) 颜色一样。如果 \(n=2\)，那么 impossible。否则可以构造出解。

最短路树

考虑一个 \(n\) 点 \(m\) 边有向图，点 \(1\) 到每个点的最短路有且仅有一条。这时候所有包含于 \(1\) 到任何一个节点最短路的边一定组成一棵树。在这棵树上可以维护一些性质，转化为树上问题。

BZOJ1576

【题意】
考虑一个 \(n\) 点 \(m\) 边有向图，边有边权。点 \(1\) 到每个点的最短路有且仅有一条。对于 \(i \le [2,n]\)，求 \(1\) 到 \(i\) 不经过这条最短路的最后一条边（终点为 \(i\) 的）的路径中最短的一条的长度。

【分析】
我们建立最短路树，根节点为 \(1\)。发现所求路径一定是这样的：先向下沿着树边走一段，然后走一条非树边，然后向上沿着树边走一段。考虑每个非树边的贡献是两个端点在树上的整条简单路径，不包括 lca。并且有贪心策略，每个点只会被一个最小的非树边更新。于是可以用并查集路径压缩。