线段树合并

WC2013课件。

• 线段树：有一列元素 \(a_1, a_2,..., a_n \in S\)，\(S\) 上有二元运算 \(+\) 满足结合律，且对于任意 \(a,b \in S\) 都有 \(a+b \in S\)，且 \(+\) 可以高效完成，如 \(O(1)\)。那么线段树支持单点修改，支持给定 \(l,r\)，回答 \(a_l + a_{l + 1} + ... + a_{r}\)。
• 区间修改：有些问题中由于 \(+\) 的特殊性可以维护区间修改，但一般情况不一定能这么做。
• 一旦定义域确定，构造的线段树形态唯一。因此可以合并两棵范围相同的线段树 \(a,b\)：

merge(a,b)
	若 a,b 中有一个不含任何元素，返回另一个。
	若 a,b 是叶子，返回 merge_leaf(a,b)
	返回 merge(a->ls,b->ls) 与 merge(a->rs,b->rs) 执行 + 操作 pushup 之后的结果。

• 注意 merge_leaf 不等同于 \(+\) 操作，他是对两个 key 相同的元素进行一定的合并操作合并为同一个 key 的元素，而 \(+\) 操作则是对两个区间做合并形成大区间的答案。
• 为了方便确定一个集合是否为空，采用动态开点的方式，若某棵子树为空，则其父亲的对应指针为空。
• 例子：维护区间内数字个数。
  
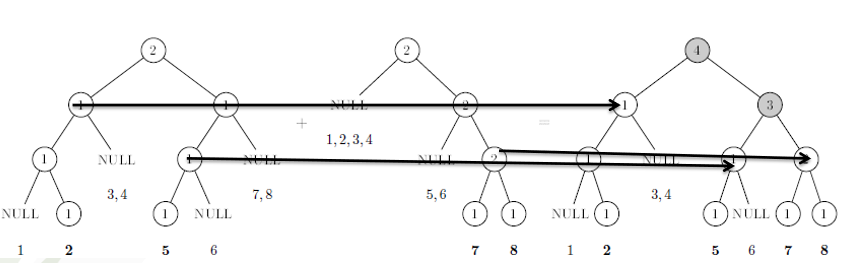
• 时间复杂度分析
  merge_leaf 和 \(+\) 都为 \(O(1)\) 则合并的开销正比于两棵树公共节点数。
  还有一个很有用的结论：若 \(n\) 棵含有单个元素的树，经过 \(n-1\) 次 merge 操作合并为 \(1\) 棵树，代价为 \(O(n \log n)\) 或 \(O(n \log U)\)（权值线段树），因为这样的操作不会比往一个空树中插入 \(n\) 个元素来得高。

P4556

回顾树上差分。我们定义树上前缀和为

\[s_i = \sum_{j \in subtree_i} a_j \]

那么

\[s_i = \sum_{j \in son_i} s_j + a_i \]

将 \(s,a\) 都降一级，那么可以将链上操作转化为单点操作。
于是我们需要在 \(q\) 时维护权值线段树的单点加，最后 dfs 一遍，将子树与自己线段树合并。由于所有点的线段树元素个数不超过 \(4n\)，所以总复杂度为 \(O(q \log n + n \log n)\)。（LCA）

注意 merge_leaf 操作是将单点计数器相加，而 \(+\) 运算是取 max。（这下能分清楚了吧）

LCA别写假了！

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int n, m; 
struct sgt {
    int ls, rs;
    int dat, ind;  //存储max和max的位置是哪个
}tree[6400010];
int root[100010], dep[100010];
vector<int> g[100010];
int anc[100010][32];
int cnt = 0;
int v = 100000;
void pre_lca(int i) {
    int k = log2(dep[i]);
    f(j, 1, k) {
        anc[i][j] = anc[anc[i][j - 1]][j - 1];
    }
}
void dfs(int now, int fa) {
    dep[now] = dep[fa] + 1;
    anc[now][0] = fa;
    pre_lca(now);
    f(i, 0, (int)g[now].size() -1 ) {
        if(g[now][i] != fa) dfs(g[now][i], now);
    }
}
int lca(int x, int y) {
    if(dep[x] < dep[y]) swap(x, y);
    int d = dep[x] - dep[y];
    int nbit = 0;
    while(d) {
        if(d & 1) x = anc[x][nbit];
        d >>= 1;
        nbit++;
    }
    if(x == y) return x;
    int k = log2(dep[x]);
    for(int i = k; i >= 0; i--){
        if(anc[x][i] == anc[y][i]) continue;
        else {
            x = anc[x][i];
            y = anc[y][i];
        }
    }
    return anc[x][0];
}
int newnode() {
    return ++cnt;
}
void pushup(int now, int ls, int rs) {
    if(tree[ls].dat >= tree[rs].dat) {
        tree[now].dat = tree[ls].dat; 
        tree[now].ind = tree[ls].ind;
    }
    else {
        tree[now].dat = tree[rs].dat; 
        tree[now].ind = tree[rs].ind;        
    }
}
void add(int now, int l, int r, int pos, int k) {
    if(l == r) {
        tree[now].dat += k;
        if(tree[now].dat > 0) tree[now].ind = pos;
        return;
    }
    int mid = (l + r) >> 1;
    if(pos <= mid) {
        if(tree[now].ls == 0) tree[now].ls = newnode();
        add(tree[now].ls, l, mid, pos, k);
    }
    else {
        if(tree[now].rs == 0) tree[now].rs = newnode();
        add(tree[now].rs, mid + 1, r, pos, k);
    }
    pushup(now, tree[now].ls, tree[now].rs);
    return;
}
int op(int now, int ls, int rs) {
    if(tree[ls].dat >= tree[rs].dat) {
        tree[now].dat = tree[ls].dat; 
        tree[now].ind = tree[ls].ind;
    }
    else {
        tree[now].dat = tree[rs].dat; 
        tree[now].ind = tree[rs].ind;        
    }    
    return now;
}
int merge(int xnow, int ynow, int l, int r) {
    //传指针
    if(xnow == 0) return ynow;
    if(ynow == 0) return xnow;
    if(l == r) {
        tree[xnow].dat = tree[xnow].dat + tree[ynow].dat;
        if(tree[xnow].dat > 0) tree[xnow].ind = l;
        return xnow;
    }
    int mid = (l + r) >> 1;
    return op(xnow, tree[xnow].ls = merge(tree[xnow].ls, tree[ynow].ls, l, mid), 
              tree[xnow].rs = merge(tree[xnow].rs, tree[ynow].rs, mid + 1, r));
}
int ans[100010];
void dfs_tree(int now, int l, int r) {

    cout << "index = " << now << ", range from:[" << l << ", " << r << "], the max number is: " << tree[now].ind << ", with " << tree[now].dat << " numbers.\n";
    if(now == 0 || l == r) return;
    int mid = (l + r) >> 1; dfs_tree(tree[now].ls, l, mid); dfs_tree(tree[now].rs, mid + 1, r);
}
void dfs_ans(int now, int fa) {
    f(i, 0, (int)g[now].size() -1 ) {
        if(g[now][i] != fa) {
            dfs_ans(g[now][i], now);
            root[now] = merge(root[now], root[g[now][i]], 1, v);
        }
    }
    ans[now] = tree[root[now]].ind;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    cin >> n >> m;
    f(i, 1, n - 1) {
        int u, v; cin >> u >> v;
        g[u].push_back(v); g[v].push_back(u);
    }
    dfs(1, 0);
    f(i, 1, m) {
        int x, y, typ; cin >> x >> y >> typ;
        int rt = lca(x, y); 
        if(rt != 1) {
            if(root[anc[rt][0]] == 0) root[anc[rt][0]] = newnode();
            add(root[anc[rt][0]], 1, v, typ, -1);
        }
        if(root[rt] == 0) root[rt] = newnode();
        add(root[rt], 1, v, typ, -1);
        if(root[x] == 0) root[x] = newnode();
        add(root[x], 1, v, typ, 1);
        if(root[y] == 0) root[y] = newnode();
        add(root[y], 1, v, typ, 1);
    }
    dfs_ans(1, 0);
    f(i, 1, n) cout << ans[i] << endl;
    time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}