后缀数组
做了 ABC270F,茅塞顿开。后缀排序,分明是抄的循环移位排序板子。
ABC270F
题意:给定两个长度为 \(n\) 的字符串 \(s,t\),求有多少个有序点对 \((i,j)\) 使得 \((s \rightarrow i) < (t \rightarrow j)\)。其中 \((s \rightarrow i)\) 表示 \(s\) 向右循环位移 \(i\) 位。其中 \(i,j \in [0,n-1]\)。
\(n \le 2 \times 10^5\)
分析:首先转化题意。将所有循环移位之后的字符串混在一起排序,所需要寻找的就是 \(rank_{(s\rightarrow i)} \le rank_{(t\rightarrow j)}\) 的个数。也就是说,混排找到 \(rank\) 就完事了。
其实后缀排序抄的循环移位排序板子。循环移位是本质。
思想就是要利用好“循环”的性质:以 \(c_i\) 开头,长度为 \(2^k\) 的字符串的后半部分也就是以 \(c_{i + 2^{k-1}}\) 开头,长度为 \(2^{k-1}\) 的字符串。
定义“第 \(i\) 层”为排好以每个位置为开头, \(2^i\) 为长度的字符串。这时我们就可以利用上一层求出的 rank,求出这一层一个 pair,也就是左半边和右半边的 rank,其中右半边的 rank 是从别的地方拿来的(合理利用信息)。
注意并不一定是 \(n=2^k\) 的才可以排序,我们最后一次排序可以类似 ST 表,有一定的重合,比如 \(n=6\),那么我们使用 \(1234~3456\) 作为上一层的 pair 的来源。可以证明这个是对的。(怎么证明:考虑讨论两个字符串中是第几位存在大小不一样的关系,然后分别看看能不能检验出来)
然后算答案,有可能会踩坑(atcoder 的数据水的要命,踩坑了也能过几十个点)。正确的做法是,先把 \(s\) 里所有 rnk 拍到桶里做前缀和,然后用 \(t\) 里的元素去找。
赛时写的是没有优化的 \(O(n \log^2 n)\) 算法。如果用基数排序可以做到 \(O(n \log n)\)。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int n;
int rnk[500010];
int pow2[500010];
vector<pair<char, int>> init;
vector<pair<pair<int, int>, int>> pk; //后缀排序用的
int calc(int i, int len) {return (i<n ? (i+len)%n : n+((i-n+len)%n));}
int cc[500010];
int ss[500010];
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin >> n;
// cout << calc(4, 2);
pow2[0]=1;
f(i,1,n)pow2[i]=pow2[i-1]*2;
string s,t;cin>>s>>t;
s += t;
int x = log2(n);
//重新标号,从 0~n-1,n~2n-1
//len=1
f(i,0,2*n-1){
init.push_back({s[i],i});
}
sort(init.begin(),init.end());
int now=0;
f(i,0,2*n-1){
if(i != 0 && init[i].first == init[i-1].first) rnk[init[i].second]=rnk[init[i-1].second];
else rnk[init[i].second]=++now;
}
// cout << "k=0"<<endl;
// f(i,0,2*n-1)cout<<rnk[i]<<" \n"[i==2*n-1];
f(k, 0, x - 1){
//排序长度为2^k
int len=pow2[k];
// cout << len << endl;
f(i,0,2*n-1){
pk.push_back({{rnk[i],rnk[(i<n ? (i+len)%n : n+((i-n+len)%n))]}, i});
}
sort(pk.begin(),pk.end());
now=0;
f(i,0,2*n-1){
if(i!=0&&pk[i].first==pk[i-1].first) rnk[pk[i].second]=rnk[pk[i-1].second];
else rnk[pk[i].second]=++now;
}
pk.clear();
// cout << "k="<<k<<endl;
// f(i,0,2*n-1)cout<<rnk[i]<<" \n"[i==2*n-1];
}
int lft = n - pow2[x];
f(i,0,2*n-1){
pk.push_back({{rnk[i],rnk[(i<n ? (i+lft)%n : n+((i-n+lft)%n))]}, i});
}
sort(pk.begin(),pk.end());
now=0;
f(i,0,2*n-1){
if(i!=0&&pk[i].first==pk[i-1].first) rnk[pk[i].second]=rnk[pk[i-1].second];
else rnk[pk[i].second]=++now;
}
f(i,0,n-1)cc[rnk[i]]++;
// f(i, 0, 2*n-1) cout<<rnk[i]<<" \n"[i==2*n-1];
// cout<<now<<endl;
f(i, 1, now) ss[i] = ss[i-1]+cc[i];
int ans=0;
f(i, n,2*n-1)ans+=ss[rnk[i]];
cout<<ans<<endl;
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
基数排序
注意 32 位机器下 define int long long 的运行有两倍常数。
基数排序和桶排序差不多。注意要保持编号的 index 从相同的位置开始,否则很难做区分!

#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
#define cerr if(false)cerr
#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
string s;
int sa[1000100], cn[1000100], rnk[1000100], y[1000100], lst[1000100], rng[1000100], dn[1000100];
void suf(){
int n = s.size(); s = s + '$'; int m = 127; //m = 字符集大小 + 5
f(i, 0, m) cn[i] = 0;
cn[0] = -1;
f(i, 0, n) cn[(int)s[i]]++;
f(i, 1, m) cn[i] = cn[i-1] + cn[i];
for(int i = n; i >= 0; i--) { rnk[i] = (cn[(int)s[i]]); }
for(int i = n; i >= 0; i--) { sa[cn[(int)s[i]]--] = i; }
f(i, 0, n) { y[i] = (sa[i] == 0 ? n : sa[i] - 1); }
f(i, 0, n) lst[i] = rnk[i];
for (int k = 1; k <= n; k <<= 1) {
f(i, 0, n) rng[i] = -1;
f(i, 0, n) cn[i] = 0;
f(i, 0, n) cn[rnk[y[i]]]++;
f(i, 0, n) cn[i] = cn[i - 1] + cn[i];
f(i, 0, n) dn[i] = cn[i] - 1;
for(int i = n; i >= 0; i --) {
rnk[y[i]] = ( cn[lst[y[i]]] -= (lst[(y[i]+k>=n+1 ? y[i]+k-n-1 : y[i]+k)] != rng[lst[y[i]]]) );
rng[lst[y[i]]] = lst[(y[i]+k>=n+1 ? y[i]+k-n-1 : y[i]+k)];
}
for(int i = n; i >= 0; i --) { sa[dn[lst[y[i]]]--] = y[i];}
f(i, 0, n) {y[i] = sa[i] < (k << 1) ? sa[i] + n + 1 - (k << 1) : sa[i] - (k << 1);}
f(i, 0, n) lst[i] = rnk[i];
}
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin >> s; suf(); int n = s.size(); f(i, 1, n - 1) {cout << sa[i] + 1 << " ";} cout << endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
后缀排序
后缀排序为什么抄的循环节排序?
考虑后缀和循环的差别是什么。后缀结束了就不会有下一个了,于是例如 \(ab\) 和 \(a\) 比较的时候因为 \(a\) 的第二位没有了,所以直接判定 \(a\) 比较小。这一点如果用循环移位在 \(a\) 之后加上个什么东西可就两说了。
所以我们为了能够统一每个字符串的长度,在每个后缀结束的时候加上一个 \(\$\) 符号,表示一个比所有字母都小的符号。然后把后面的循环补上来,可以发现最终排序的就是一堆循环移位字符串。
后缀数组的应用
后缀排序后的数组能解决的问题还很有限,但是如果加上一个名为 \(height\) 的数组,那么就能发挥后缀数组的强大功效了。
\(height_i\),表示 \(i\) 与 排序过后 \(suff_i\) 的上一个串之间的最长公共前缀。
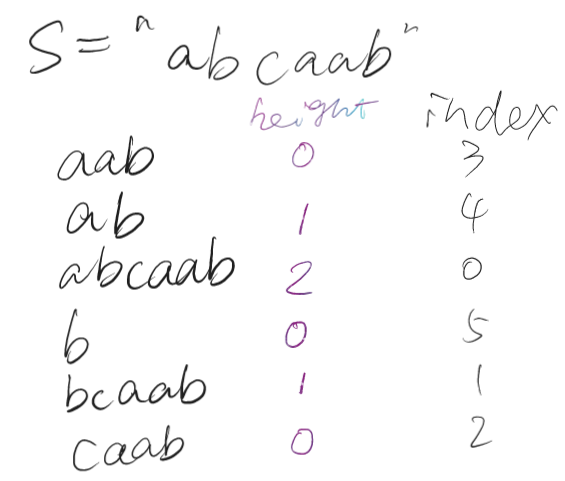
暴力求显然为 \(O(n^2)\)。但是有一个性质使得我们可以 \(O(n)\) 构建:\(\forall i \ge 1, height_i \ge height_{i - 1} -1\)。首先考虑正确性证明。考虑第 \(i - 1\) 个后缀。它前面的一个串和它的前 \(k\) 个字符都相同。那么令这个字符串为 \(t\)。如果 \(k = 0\) 或者 \(k = 1\),那么显然成立。否则,考虑 \(t\) 去掉首字母之后和第 \(i\) 个后缀一定有 \(k-1\) 的相似度。并且如果存在同样靠前且相似度更大的串,靠前的相似度更小的串一定不会排在相邻的位置。
因此我们从 \(0 \sim n - 1\) 来求 \(height_i\)。由于指针只会往回跳 \(O(n)\) 次,和 KMP 的证明类似,时间是 \(O(n)\) 的。
来看应用。
求 \(s\) 两个后缀的最长公共前缀
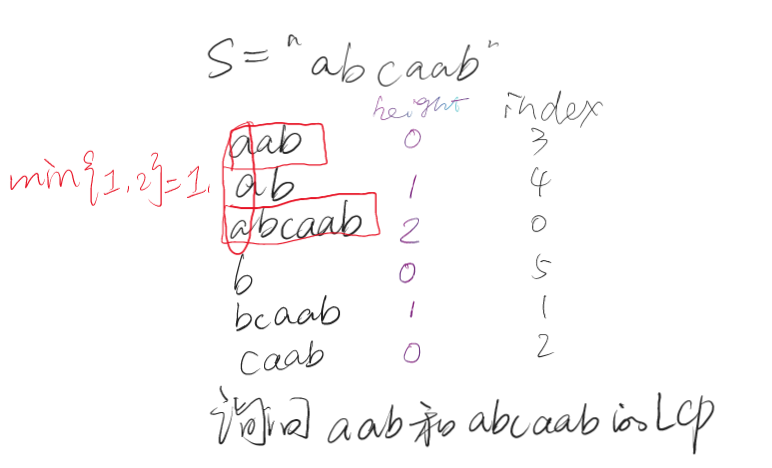
只需找到排完序之后两个数的位置,然后做区间 RMQ 即可。由于相似度问题,排在它俩中间的串,与它俩之间任何一个串的公共前缀不会比它俩之间的小。并且也不会所有它俩中间的串的 \(height\) 比最长公共前缀还长。
求最长重复子串(可重叠)
也就是 \(height\) 的最大值。
求最长重复子串(不可重叠)
二分答案。对于 \(k\),检验的时候把所有 \(height \ge k\) 的分成一段,看这一段里面有没有 \(index\) 相差超过 \(k\) 的。

找具体的串是简单的。
求重复 \(k\) 次的子串(可重叠)
分段之后,考虑是否有超过 \(k\) 个元素的段。


