面积相关公式与定理
正弦定理
在任意 \(△ABC\) 中,角 \(A、B、C\) 所对的边长分别为 \(a、b、c\),三角形外接圆的半径为 \(R\),直径为 \(D\)。则有:
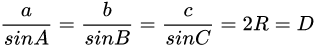
余弦定理

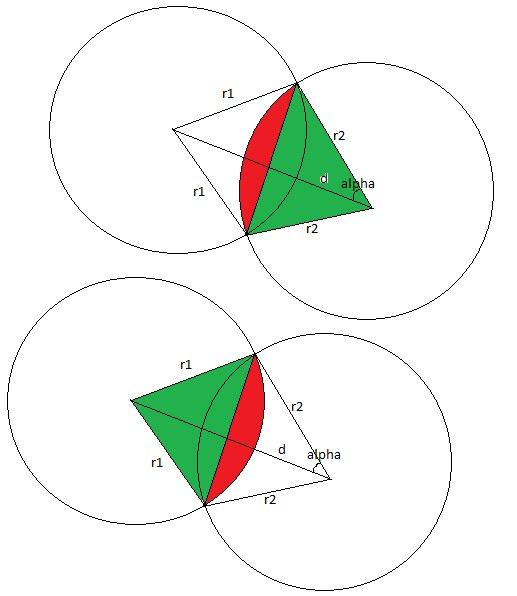
圆形面积交
CF600D
求圆形面积交。
如果相离或内含,随便求即可。
如果相交:
设 \(d\) 表示连心线长度。
在三角形 \(r1-r2-d\) 中由余弦定理有 \(\alpha = \arccos(\cfrac{-r_1^2 + r_2^2 + d^2}{2r_2 d})\)。
那么 \(S_交 = S_{扇1} + S_{扇2} - S_{▲1} - S_{▲2}\)
\(S_{扇2} = \alpha r_2^2,S_{▲2} = \frac{1}{2} r_2^2 \sin \alpha\)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for (int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(), i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef long double ld;
const int inf = 1e9;
ld pi = acos(-1);
ld deg(ld x) { return x * 180 / pi; }
ld dis2(ld x1, ld x2, ld y1, ld y2)
{
return (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
// think twice,code once.
// think once,debug forever.
cout << fixed << setprecision(12);
ld x1, y1, r1, x2, y2, r2;
cin >> x1 >> y1 >> r1 >> x2 >> y2 >> r2;
if (r1 > r2)
{
swap(x1, x2);
swap(y1, y2);
swap(r1, r2);
}
if (dis2(x1, x2, y1, y2) >= (r1 + r2) * (r1 + r2))
{
cout << 0 << endl;
}
else if (dis2(x1, x2, y1, y2) <= (r2 - r1) * (r2 - r1))
{
ld s = pi * r1 * r1;
cout << s << endl;
}
else
{
ld s = 0;
ld d = sqrtl(dis2(x1, x2, y1, y2));
ld alpha = 2 * acos((r1 * r1 + d * d - r2 * r2) / (2 * r1 * d));
s += (1.0 / 2 * alpha * r1 * r1 - 1.0 / 2 * r1 * r1 * sin(alpha));
ld beta = 2 * acos((r2 * r2 + d * d - r1 * r1) / (2 * r2 * d));
s += (1.0 / 2 * beta * r2 * r2 - 1.0 / 2 * r2 * r2 * sin(beta));
cout << s << endl;
}
time_t finish = clock();
// cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}


