斜率优化

斜率优化是将一类 \(O(n^2)\) 的 DP 状态转移优化至 \(O(n \log n)\) 甚至 \(O(n)\) 的方法。

用一个 atcoder dp contest 的最后一题来讲解：

dp_z Frog-3

https://atcoder.jp/contests/dp/tasks/dp_z

题意：有 \(n\) 个石头，一只青蛙初始站在第 \(1\) 块上。它可以执行若干次以下操作：

• 跳到第 \(j(i < j \le n)\) 块石头上，并花费 \((h_i - h_j) ^ 2 + c\) 的代价。

求青蛙到达第 \(n\) 块石头的最小代价。

\(2 \le n \le 2 \times 10^5, 1 \le c \le 10^{12}, \mathbf{1 \le h_1 < h_2<...<h_n\le 10^6}\)

分析：

令 \(dp_i\) 表示走到第 \(i\) 块石头的最小代价。

不难写出状态转移方程：

\[dp_i = \min_{j < i} \{dp_j + (h_j - h_i)^2 + c\} \]

也就是找到在这个式子 \(dp_i = dp_j + (h_j - h_i)^2 + c\) 中使得 \(i\) 最小的 \(j\)。

为了使用斜率优化，我们需要将其转化为 \(y = kx + b\) 的形式，其中 \(x\) 和 \(y\) 是只和 \(j\) 有关的式子，\(k\) 是只和 \(i\) 有关（已知）的式子。而 \(b\) 和 \(dp_i\)（未知）有关，需要最小化。也就是说，在平面上分布有若干个点 \((x_j, y_j)\)，需要找到一个点，使得经过这个点的直线与 \(y\) 轴的交点最小。（截距最小）

即：

\[\color{red}{dp_j + h_j^2} = \color{blue}{2h_j}\color{green}{h_i}+\color{purple}{dp_i - h_i - c} \]

\[\color{red}y = \color{blue}k \color{green}x + \color{purple}b \]

例如这个题目假设 \(h_1 = 1,h_2 = 2\)，我们求出了 \(dp_1 = 0, dp_2 = 7\)，那么平面上分布有两个点 \((x_1,y_1)=(1,1)\) 和 \((x_2,y_2)=(2,11)\)：

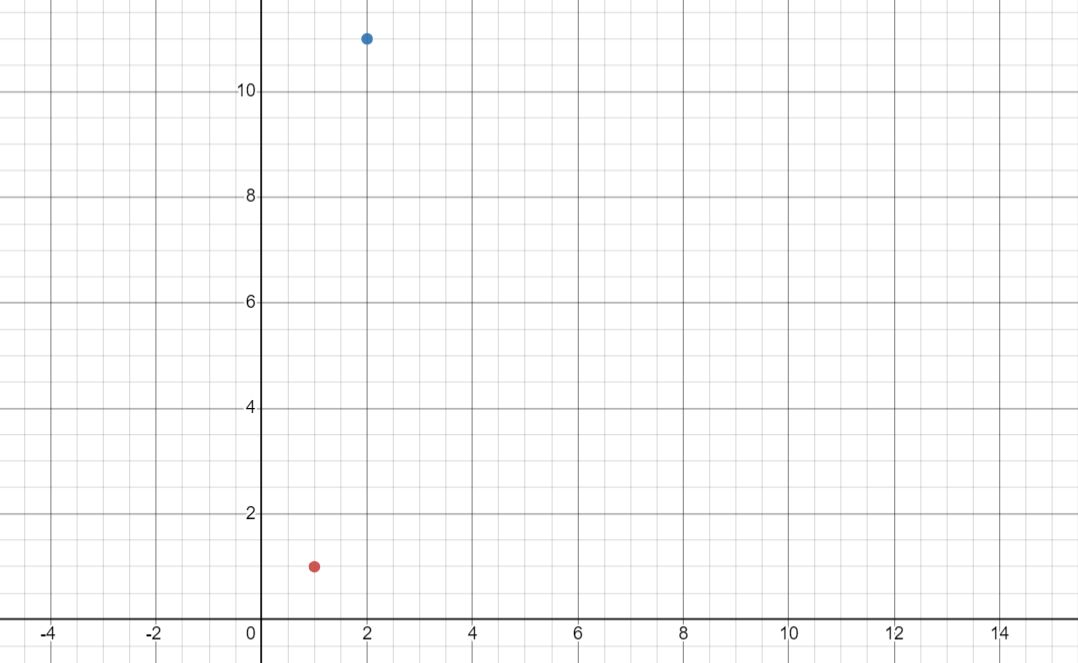
现在要求出 \(dp_3\)，并且 \(h_3 = 3\)。以 \(2h_3=6\) 为斜率，画出两条线，分别是 \(j=1\) 和 \(j=2\) 时候对应的线：

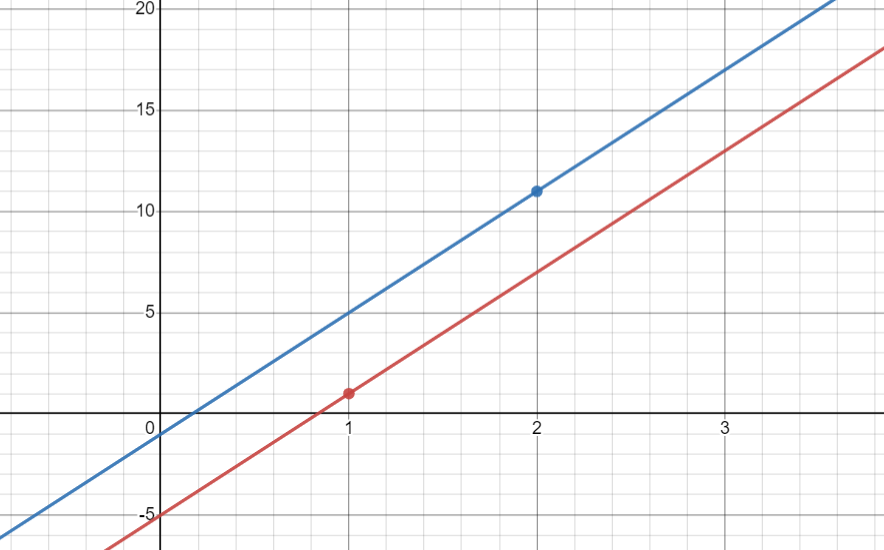
可以发现是 \(j=1\) 的时候斜率更小，因此更优的决策点应该是 \(j=1\)。

咱们连接一下这两个点，会发现因为两个点的斜率比 \(k_3\) 大，所以第一个点是最优决策点。如果换一个斜率比两点之间斜率大的点，那么第二个点会变成最优决策点。

再往外探索，发现如果三个点长成下图这样，那么 \(B\) 点一定不会是最优决策点：

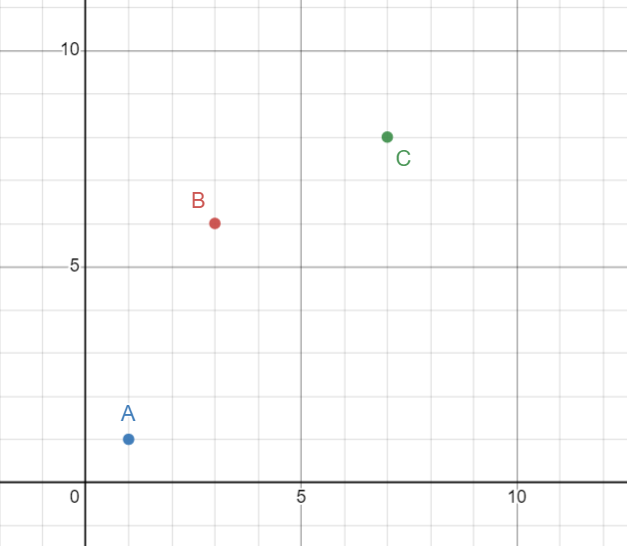
因为 \(k_{AB} > k_{BC}\)，或者说，\(B\) 不在凸包上。那么我们考虑维护一个凸包（下凸壳），即若干个点的集合，其中每相邻两个点的斜率依次递增。如下图，凸包就是 \(\{A,D,C,E\}\)。

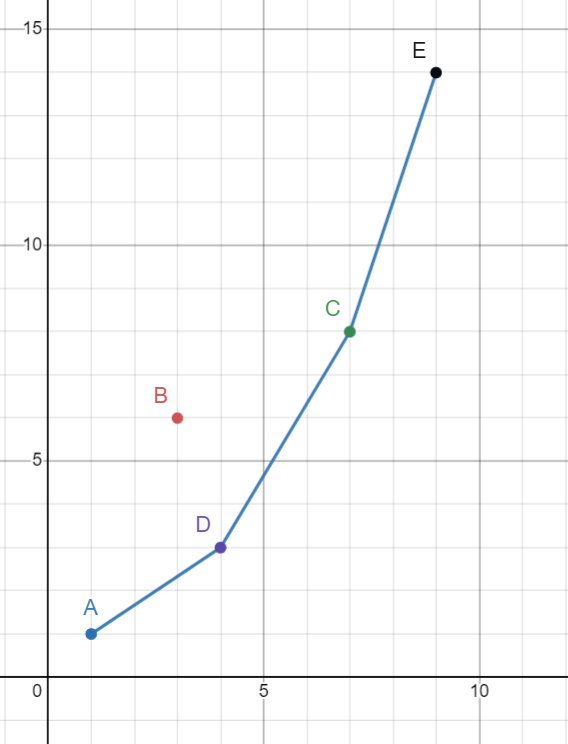
当我们想要求一个新的直线 \(y = k_px + b\) 的最优决策点时（决策点不止一个，也就是凸包必然包含两个以上点的时候），需要找到点 \(i\) 使得 \(k_{i-1,i} < k\) 且 \(k_{i,i+1} > k\)。（这里如果不存在这样的点，那么如果 \(k_{12}>k\) 那么 \(1\) 是最优决策点，如果 \(k_{m-1,m} < k\) 那么 \(m\) 是最优决策点（\(m\) 为现有凸包大小））这个可以使用二分做到。

算完 \(p\) 的 \(dp\) 值，在队尾加入这个新点的时候，为了维护凸包不断弹出队首直到：\(k_{m-1,m} < k_{m,(x_p,y_p)}\) 或 \(m=1\)（\(m\) 为现有凸包大小）

如此这样算下去，我们就做完了整个 DP 过程，时间复杂度 \(O(n \log n)\)。

一般化的使用场景

对于

\[dp_i = b_i + \max_{j \le R_i} \{x_jk_i + y_j\} \]

（即 \(y_j = -k_ix_j + dp_i - b_i\)）
其中 \(R_i\) 是 递增序列，\(x_j\) 是递增序列时可以使用斜率优化将 \(O(n^2)\) 的转移优化至 \(O(n \log n)\)。

要点

• 比较斜率时，应使用十字相乘法，避免精度丢失。
• 应将初始元素先放进凸包去，如这题的 \(dp_1 = 0\)，就应该放进 \((h_1,h_1^2)\)；
• 可以用 \(O(n^2)\) 的暴力对拍。
• 在“一般化的使用场景”下，当 \(k\) 有单调性的时候，可以不用二分查找，例如 \(k\) 单调增的话，每次直接删除队头的元素直到 \(k_{1,2}>k\)，因为如果 \(k_{1,2} < k\)，之后更不会用到第 \(1\) 个点做最优决策点。然后直接取队头元素即可。\(k\) 单调减的话取队首即可，相类似。此时的复杂度可以优化到 \(O(n)\)。
• “一般化的使用场景”还可以继续扩展：
  如果 \(x_j\) 不是单调递增序列，那么相当于是要在凸包的中间插入点。如下图：
  
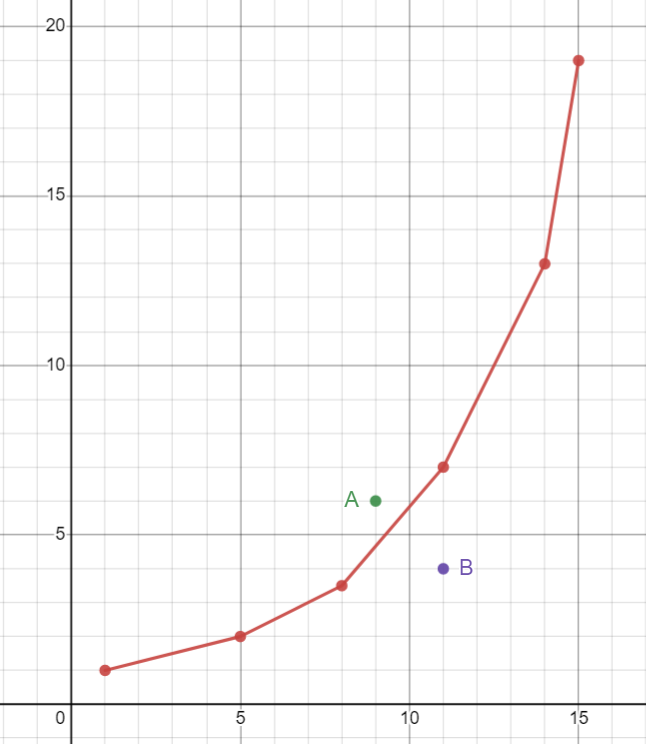
  这时需要使用一个平衡树维护，以 \(x\) 为第一关键字：
  我们首先判断这个点在不在凸包上。找到左边和右边的点，看看斜率是否是左边大于右边。如果不是的话（例如点 \(A\)）那么它不在凸包上，不需要插入。
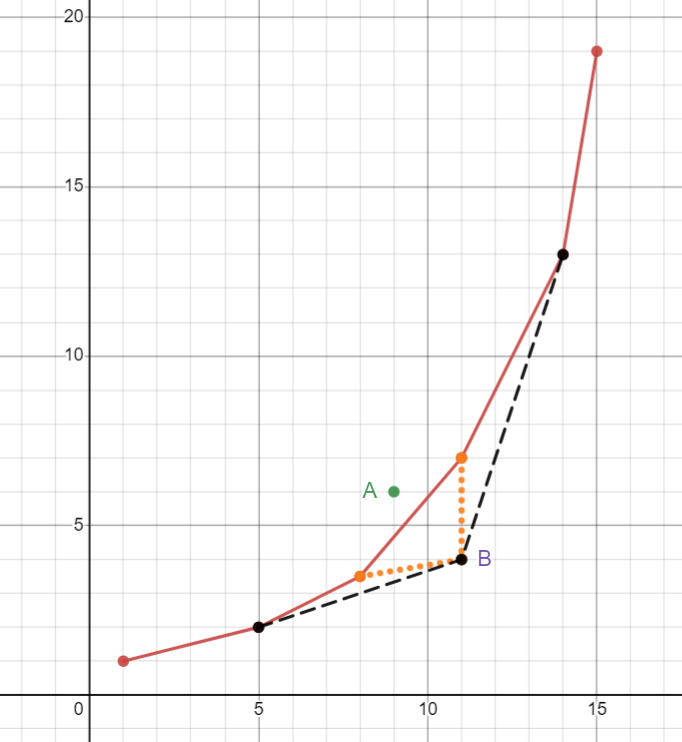
  如果是的话，那么需要找到左边和右边的后继节点，分别在平衡树上二分，判定条件是左边的斜率小于右边的斜率。如下图，黑色的边是新的凸包中的边。
  时间复杂度 \(O(n \log n)\)。
  
  如果 \(R\) 不是单调递增序列，写主席树+线段树二分，等作者水平提高再来学习。