基础数论
lcm 不能用作变量名。
下文中 \(a/b\) 指整数除法,即 \(a=kb+r\) 那么 \(a/b=k\)。
常见转化(有启示意义)会用 \(\mathbf{mathbf}\) 加重显示。
1 基础工具
1.1 缩系
对于整数 \(p\),记 \(S = \{x|(x,p) = 1\}\) 为 \(p\) 的缩系。
性质:缩系中任意两个元素相乘,结果仍在缩系中。
证明:\((x,p) = 1, (y,p) = 1 \rightarrow (xy, p) = 1 \rightarrow (xy \% p, p) = 1\)
性质:缩系整体乘上 \(x \in S\),仍然构成缩系。
证明:由上一个结论得知,乘法之后的任意一个数仍在缩系中。现在证明这些数不会重复:
假设 \(ax \equiv bx(\bmod p)\),那么有 \((a-b)x + kp = 0\)。注意这里 \((a-b), p, k\) 都是变量。又因为 \((x, p) = 1\),故 \(((a-b), p) = 0\),也就是 \(a\) 和 \(b\) 相同。
1.2 欧拉定理
对于 \(\gcd(a, n) = 1\),有 \(a^{φ(n)} \equiv 1(\bmod n)\)。证明:
考虑 \(n\) 的缩系 \(\{S_1,S_2,...,S_m\}\),有 \(S_1a \times S_2 a \times ... \times S_m a \equiv S_1S_2...S_m(\bmod m)\)(缩系性质)
1.3 扩展欧拉定理
\(a^{2φ(n)} \equiv a^{φ(n)}(\bmod n)\)。
也就是:
这两个可以相互推导。我们先看看应用:光速幂。
对于 \(a,n\) 固定的 \(a^b \bmod n\),我们有 \(O(\sqrt n)\) 预处理,\(O(1)\) 解决的方法,也就是用欧拉定理降幂。
考虑降到 \(b < 2φ(n)\) 的范围。然后考虑分块,类似 BSGS 的思想,\(a^b = a^{(k \times \lceil\frac{b}{k} \rceil)} \times a^{b \bmod k}\)。预处理 \((a^k)^j\) 和 \(a^j\) 即可。
考虑证明。
https://www.bilibili.com/video/BV1tu411Z7Bj/
感性理解:都是像这样的一个环状结构:

例如:\(p = 120, a = 18\) 的时候,\(\{a^i\} = :\)
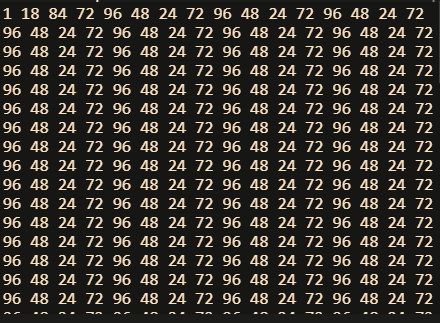
1.4 逆元
给定 \(a,b\),求 \(a \times a^{-1} \equiv 1(\bmod b)\) 的解,即为 \(a\) 模 \(b\) 意义下逆元。其存在当且仅当 \(\gcd(a, b) = 1\) 成立(裴蜀定理)。
那么一切满足该条件的数,逆元可以使用 exgcd 求出。(P1082)
另外,可以用欧拉定理求出,因为 \(a^{φ(p)} \equiv 1(\bmod p)\),所以 \(a \times a^{φ(p)-1} \equiv 1(\mod p)\),所以 \(a^{-1} \equiv a^{φ(p)-1}(\bmod p)\)。如果 \(O(n)\) 预处理,还是得 \(\log n\) 快速幂,和 exgcd 一样。
特别地,当 \(p\) 为素数时,有 \(φ(p) = p-1\),这样就可以 \(O(\log n)\) 直接快速幂求。
我们还可以线性求一串数的逆元,公式:
- \(1^{-1} \equiv 1(\mod p)\)
- 现在要求 \(i\) 模 \(p\) 下的逆元,设 \(p = i \times k + r, k = p / i, r = p \% i\)。
则 \(i \times k + r \equiv 0(\mod p)\)
等式两边同时乘 \(i ^ {-1} \times r ^ {-1}\) 得:
\(k \times r^{-1} + i^{-1} \equiv 0(\mod p)\)
即:
\(i^{-1} = -(p / i) \times (p \% i)^{-1} (\mod p)\)。
那么我们可以由比 \(i\) 小的数的逆元推得 \(i^{-1}\)。
代码:
int n, p;
int inv[3000010];
int main() {
cin >> n >> p;
inv[1] = 1;
cout << inv[1] << endl;
f(i, 2, n) {
inv[i] = ll(p - p / i) * inv[p % i] % p;
cout << inv[i] << endl;
}
return 0;
}
逆元的性质:对于质数 \(p\),其缩系 \([1,p-1]\) 中逆元为自身的(\(x \times x \equiv 1(\bmod p)\)) 的数只有 \(1\) 和 \(-1\),其余 \(p-3\) 个数的逆元两两对应。
证明:由上述知道 \(x\) 模 \(p\) 的逆元一定存在,且模 \(p\) 唯一。(为何唯一?考虑 \(x \times x^{-1} + p \times y = 1\) 的通解形式为 \(x^{-1} = x^{-1}_0 + ap\))故如果“逆元为自身的(\(x \times x \equiv 1(\bmod p)\)) 的数只有 \(1\) 和 \(-1\)” 成立那么原命题成立。
事实上,这句话是成立的。考虑因式分解:\((x-1)(x+1) \equiv 0(\bmod p)\)。对于 \(p\) 是素数,只可能这两个的其中一个模 \(p\) 余 \(p\),否则没有其他方法。于是只有 \(x = 1\) 或者 \(x = -1\)。
事实上,这个东西可以引申出“二次探测定理”:如果 \(x\) 不是质数,那么还可能有其他方案,比如 \(8 = 2 \times 4\),那么有 \((3-1)(3+1) \equiv 0(\bmod 8)\),那么 \(3\) 也是一个解。如果存在这样的解,那么一定不是素数。该定理构成了 Miller-Rabin 算法的其中一部分。
一种简单好用的求任意互质 \(a, b\) 间 \(\rm {inv}(a, b)\) 的方式:
int inv(int a, int b) {
return a > 1 ? b - inv(b % a, b) * b / a : 1;
}
首先重申 \(\rm{inv}(a, b) = \rm{inv}(a % b, b)\)。你首先放进去的 \(a\) 确保它处于 \([1, b - 1]\),不管是什么做法都需要先做这个,否则爆 ll。
然后考虑上面这个代码的原理。假设你求出了 \(\rm{inv}(b,a) = t\)。那么令 \(q = \cfrac{tb - 1}{a}\),有 \(aq + 1 \equiv 0(\bmod b)\),所以 \(-q\) 是逆元。
因为 \(\cfrac{bw}{a} = \cfrac{bw-1}{a}\),所以上式是对的。
一个题外话:C++ 除法向 0 舍入,所以不管把上面理解为 b - inv(b % a, b) * b / a 还是 b + (- inv(b % a, b) * b / a) 都有一样的结果,除法这块很关键,别向下取整给写成向 0 舍入就寄了。
1.5 \(O(n + \log p)\) 求 \(n\) 个数关于 \(p\) 的逆元
考虑先求出 \(s = \prod a_i\) 的逆元,然后乘上一段前缀积和后缀积即可。
这个可以运用到预处理阶乘逆元中,代码如下:
f(i,1,V+1) {jc[i]=jc[i-1]*i%mod;} inv[V+1]=qpow(jc[V + 1], mod - 2);
for(int i = V; i >= 1; i --) inv[i] = inv[i + 1] * (i+1) % mod;
这十分重要,对于值域 \(10^7\) 的阶乘逆元需要这个。
1.6 Exgcd (扩展欧几里得算法)(求解二元一次不定方程/单个线性同余方程)
引理 1:\(gcd(a,b)=gcd(b,a \bmod b)\)
证明:
令 \(gcd(a, b) = g\),设 \(a=g \times k_1, b = g \times k_2\)。
那么 \(\mathbf{a \% b = (k1 \% k2) \times g}\)。
因为都有公因子 \(g\),所以 \(b\) 和 \(a \bmod b\) 之间一定有公因子 \(g\)。
要证最大公因数是 \(g\) 只需证 \(k1 \% k2\) 和 \(k2\) 互质。
反证法:假设它们之间有公因数 \(t>1\),设 \(k1 \% k2 = t \times q, k2 = t \times p\)。
那么 \(a = g \times (ktp+tq)\) 有因子 \(t\),同时 \(b = g \times tq\) 也有因子 \(t\),与假设矛盾。
故原命题成立。
或者使用 \(gcd(a, b)=gcd(a, a+b)\) 推得。
现在我们要做的事情是解同余方程 \(ax \equiv k \pmod b\),其等价于二元一次不定方程 \(ax + by = k\)。
引理 2(即 exgcd 原理):上述方程对于 \(k | gcd(a, b)\) 总有整数解,否则总没有整数解。
证明:
第二句话显然成立,不论 \(x,y\) 取得什么值,\(ax+by\) 一定会有因子 \(g\)。
为了证明第一句话,并求出这个方程的解,我们考虑 \(k = gcd(a, b)\)。
我们已经证明出引理 \(1\),那么可以将 \(ax + by = gcd(a, b)\) 规约成另一个方程 \(bx' + (a\%b)y' = gcd(b, a \% b)\),方便递归计算:
我们现在假设求出了第二个方程的解,那么 \(bx' + (a - (a/b)
\times b)y' = g\)
也即 \(ay' + b(x' - (a/b)y') = g\)
因此第一个方程的解为:
\(x = y'\)
\(y = x' - (a/b)y'\)
当 \(b=0\) 时,\(x=1,y=0\) 即函数出口,因此可以得出解。
当 \(k = k' \times gcd(a, b)\) 时,只需要将 \(x,y\) 的值都对应乘上 \(k\) 即可。
以下为模板(传引用是为了在求解第二个方程之后直接把 \(y'\) 写入 \(x\),把 \(x'\) 写入 \(y\),那么只需要改一个值,就是 \(y -= (a-b) \times x\) 即可。
考虑一般的二元一次不定方程 \(ax+by=c\),考虑将方程两边同事除以 \(\gcd(a,b)\),解不变,因此有原方程的通解等同于方程 \(\cfrac{a}{\gcd(a,b)}x + \cfrac{b}{\gcd(a,b)}y = \cfrac{c}{\gcd(a,b)}\) 的解。求出该方程的特解 \(x_0, y_0\)(也就是 \(\cfrac{c}{\gcd(a,b)} \times\) (\(\cfrac{a}{\gcd(a,b)}x + \cfrac{b}{\gcd(a,b)}y = 1\) 的解),则有通解
注意,exgcd 求出的解其实是有性质的!
性质是什么呢?
对于 \(ax +by = \gcd(x, y)\),其解 \(a_0, b_0\) 满足 \(|a_0| \le y, |b_0| \le x\)。因此只需要判断是否小于 \(0\) 并做最多一次加法即可。
我们这样写,分两步走,可以求出 \(a_0,b_0, T_a, T_b\) (或者最小非负 \(a_0\),这个对一些最优性问题很重要):
const int inf = 1e9;
struct jie {
int x, y, tx, ty;
jie() {x = -inf, y = -inf, tx = 0, ty = 0;} //这是无解返回的情况。
jie(int x, int y, int tx, int ty): x(x), y(y), tx(tx), ty(ty) {}
};
void exgcd(int a, int b, int &x, int &y) {
if(!a){x=0,y=1; return;}
else {exgcd(b%a, a, y, x); x -= (b/a) * y;}
}
jie eqfc(int a, int b, int x, int y, int k) { //ax + by = k, ab 是常数,a<b
int g = __gcd(a, b);
if(k % g != 0) {return jie();}
else {
int xz, yz; exgcd(a, b, xz, yz); if(xz < 0) xz += b / g, yz -= a / g; //这里是为了让 xz 非负并且最小
return jie(xz, yz, b / g, a / g);
}
}
P1082
求 \(ax \equiv 1 \pmod b\) 的最小正整数解。
\(a,b \le 2 \times 10^9\)
也就是上面介绍过的 exgcd 求逆元。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int g, x, y;
void exgcd(int a, int b, int &x, int &y) {
if(b == 0) {
x = 1; y = 0; g = a;
return;
}
exgcd(b, a % b, y, x);
y -= (a / b) * x;
return;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int a, b; cin >> a >> b;
if(a <= b) {
exgcd(a, b, x, y);
cout << ((x % b + b) % b) << endl;
}
else {
exgcd(b, a, x, y);
cout << ((y % b + b) % b) << endl;
}
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
1.7 中国剩余定理(CRT)(解一次同余方程组)
中国剩余定理用于解决形如
在 \(m_1,...,m_n\) 互质的情况下,这个方程可以用中国剩余定理解出,具体是像拉格朗日插值公式那样构造其他项都和一个式子的答案无关,只有一项和这个式子的答案有关的东西。
我们记 \(M_i\) 为 \(\prod \limits_{j = 1} ^ n [j \neq i] m_i\)。这个东西有什么性质?它是 \(m_1,m_2,...,m_{i-1},m_{i+1},...,m_n\) 的倍数,却不是 \(m_i\) 的倍数。
我们令 \(t_i\) 为 \(M_i\) 模 \(m_i\) 的逆元。由于 \(\gcd(M_i,m_i)=1\),逆元一定存在。这个东西有什么用?\(M_it_i \equiv 1(\bmod M_i)\)。
于是当 \(x = \sum \limits_i ^ n M_i t_i a_i\) 的时候,显然满足所有式子。
考虑解的周期是什么。对于 \(x',x\) 两个解,一定满足:\(m_i|x'-x,i \in [1,n]\)。因此 \(\operatorname{lcm}(m_i)=\prod m_i | (x'-x)\) 成立。
或者用二维循环坐标系的角度看待。假设出生点在 \((0, 0)\),最小走几步可以走回去呢?这中间的每一步到达的位置都不同。显然走 \(\mathrm{lcm}\) 步可以到达。
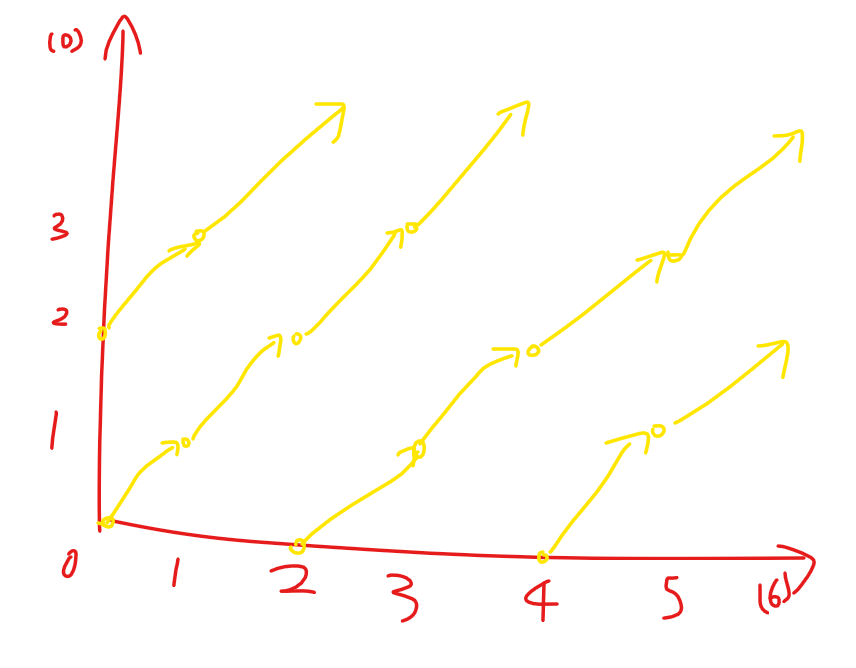
也可以看出一些斜线上的位置可以到达,一些斜线上的不能到达。斜线由 \(x - y = k\) 表示,那么 \(k | \gcd\) 的斜线是可以到达的。
(二维循环坐标系是具象化了两个质数一起构成的剩余系里面坐标移动的规律,要知道考虑)
那么通解为:
如果 \(m_i\) 不互质?由于没有办法用逆元,需要用别的方法。考虑合并两个式子可以不可以:
有解的充要条件是存在 \(k_1,k_2\) 使得
那么考虑扩展欧几里得解出 \(k_1,k_2\)。
根据上述 exgcd,需要直接解出
的解。(记得扩欧解出来的解需要放大 \(\cfrac{a_{i+1}-a_i}{\gcd(m_i,m_{i+1})}\) 倍)假设为 \((p,q)\)。那么:
其中 $ \cfrac{m_im_{i+1}}{\gcd(m_i,m_{i+1})} =\operatorname{lcm}(m_i,m_{i+1})$,因此可以化简:
很简洁。
注意两个地方:
- 当 \(\gcd(m_1, m_2) | (a_2 - a_1)\) 的时候无解。
- \(\mathrm{lcm}\) 是不可能为 \(0\) 的,如果你发现要特判 \(0\),应该是搞错了 \(a\) 和 \(m\) 的位置。
另外对于三个数以上的 exCRT 是否有解的问题,应该在多维循环坐标系上考虑,应该不会有能够比较快速计数的方式,所以一直合并是足够的。(指的是相比之下,CRT 的有解数的个数更方便计数这样)
1.8 BSGS(Baby Step Giant Step)(解未知数在指数位置且模数为质数的同余方程)
BSGS 算法用于解决形如 \(b^x \equiv n \pmod p\) 的 \(x\) 的问题或报告无解,其中 \(p\) 为质数。
怎么做呢?考虑暴力。我们可以暴力枚举指数,枚举到哪里呢?
首先我们有 \(b^0 \equiv 1\pmod p\),然后我们有欧拉定理 \(b^{φ(p)} \equiv 1 \pmod p\)。因此 \(\mathbf{b^x \pmod p 的值对 x 有循环节 φ(p) + 1}\)。
所以我们只需要枚举 \([0,p-1]\) 即可。时间复杂度 \(O(p)\),但我们可以优化算法:
假设方程的解 \(x = i \sqrt p - j(j \in [1, \sqrt p])\),那么有 \(b^{i \sqrt p - j} \equiv n \pmod c\)。两边同除 \(n\),得:\(\cfrac{b^{i \sqrt p}}{b^j \times n} \equiv 1 \pmod p\),即 \(b^{i \sqrt p} \equiv b^j \times n \pmod p\)。
右边的 \(j \in [1,\sqrt p]\) 可以 \(O(\sqrt p)\) 预处理到哈希表里(key 为数值,value 为 \(j\)),枚举 \(i \in [1, num]\) 的时候如果哈希表 key 为左边的表内有 value,那么找到了一个解。(类似分块的思路,其中块长 \(len = \sqrt p\),块数 \(num = \frac{p}{\sqrt p} + [\sqrt p \nmid p]^?\)
其中预处理阶段就是 \(\mathtt{Baby Step}\),枚举阶段就是 \(\mathtt{Giant Step}\),时间复杂度 \(O(\sqrt p \log n)\),如果使用 map 则多乘一个 \(\log p\)。
那么通解就是所有找到的在 \([0,n-1]\) 的解加上 \(k \times p(k \in \Z)\)。
需要指出的是,由于欧拉定理的适用条件为 \(\gcd(b, p) = 1\),所以只要 \(\gcd(b, p) = 1\) 都使用 BSGS 算法。
P3846
题意:求该方程的最小非负整数解,并判断无解。
\(2 \le b,n < p < 2^{31}\)。
分析:如果是要求找最小非负整数解,那么在哈希表上直接把后面的覆盖前面的即可(因为需要 \(-j\) 最小),并且找到解了直接退出即可。一直没有找到解就是无解。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int p, b, n;
map<int, int> h;
int qpow(int x, int k){
int ans=1;
while(k){
if(k&1)ans=ans*x%p;
x=x*x%p;
k>>=1;
}
return ans;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin >> p >> b >> n;
int len = sqrt(p);
int num = p / sqrt(p);
if(num * len < p) num++;
f(i, 1, len) {
h[qpow(b, i) * n % p] = i;
}
int ans = -1;
f(i, 1, num) {
int key = qpow(b, i * len);
if(h.count(key)) {
ans = i * len - h[key];
cout << ans << endl;
return 0;
}
}
if(ans == -1) cout << "no solution\n";
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
P4861
题意:求 \(k^x \equiv 1 \pmod p\) 的最小正整数解,其中 \(p\) 不一定是质数。
\(k, p \le 2 \times 10^9\)
分析:没有保证 \(\gcd(k, p) = 1\),不符合费马小定理的条件怎么办?
其实如果有解都保证 \(\gcd(k, p) = 1\)。为什么?引理 \(1\)!
我们的式子相当于 \(k \times k^{x-1} + p \times q = 1\),那么只有 \(\gcd(k, p) = 1\) 的时候有解。
因此还是可以使用 BSGS。
P3306&ABC270F
题意:有递推式
求使得 \(X_i \equiv g\) 的最小 \(i\)。
分析:
- 推一推式子可以推出通项公式。
- 然后移项转化为 \(a^i \equiv ... \pmod p\) 的形式,然后就可以用 BSGS。
- 注意 \(a=0\) 和 \(a=1\) 的时候等比数列公式不一样,要特判。
- 其中 \(a=1\) 的时候用逆元或者 exgcd 可以求。
- 注意取模的时候一旦有乘法就 \(\%p\),一旦有减法就 \(+p\)。(被这东西坑了一早上)
1.9 gcd 相关
首先要熟悉几个转化:
\(\gcd (a,b) = \gcd(a, a + qb)\)
\(\gcd (a, b) = \gcd(a, a - b)\)
\(\gcd (a, b) = \gcd(a, a \% b)\)
这几个转化很常见。
还有:
\(\operatorname{lcm}(a, \gcd(b, c)) = \gcd(\operatorname{lcm}(a, b), \operatorname{lcm}(a, c))\)
\(\gcd(a, \operatorname{lcm}(b, c)) = \operatorname{lcm}(\gcd(a, b), \gcd(a, c))\)
主要是依据 \(p\) 进赋值序列。
CF1717E
求 \(\sum \limits_{a+b+c=n} \operatorname{lcm}(c, \gcd(a, b))\)。
暴力枚举 \(c\),然后 \(a+b=n-c\)。利用第一个转化发现原式 \(= \sum \limits _{a \in [1, n - c - 1]} \operatorname{lcm}(c, \gcd(a, n - c))\)。
这时候要用到一个经典的例题(本题重中之重):计算 \(a \in [1, n-c-1], \gcd(a, n-c)\) 为各个数的 \(a\) 的方案数。
首先,\(\gcd(a, n-c)\) 肯定是 \(n-c\) 的因子。那么我们枚举 \(\gcd\),假设为 \(g\),那么如果 \(\gcd(a, n-c) = g\),\(a\) 要满足:\(a | g, (a / g) ⊥ ((n-c) / g)\)。
刚好,我们把 \(1 \sim n-c-1\) 中所有整除 \(g\) 的数除了 \(g\) 之后的取值映射到 \(1 \sim (n-c) / g\) 中,并且需要与 \((n-c) / g\) 互质。方案数显然是 \(\phi((n-c)/g)\)。
需要注意,当 \(g = n-c\) 时算出来的 \(\phi\) 为 \(1\),但这个 \(1\) 其实是 \(a = n - c\) 贡献的,不符合要求,不能计算。
1.10 因子个数
https://codeforces.com/contest/1744/problem/E2
CF1744E.Divisible Numbers
一般我们估计复杂度的时候认为因子数的上界是 \(O(\sqrt n)\),但是这个上界是比较松的。
\(10^{18}\) 以内的数最多有 \(103680\) 个因子,\(10^9\) 以内的数最多有 \(1344\) 个因子。
为什么呢?我们不妨考虑估计一个更紧的上界。
对于 \(x = p_1^{\alpha_1}...p_k^{\alpha_k}\),其因子个数为 \(\prod \alpha_i\)。如果我们给 \(x\) 乘以一个它已经拥有的质因子 \(p_j\),那么因子个数会加上 \(\cfrac{\prod \alpha_{i}}{\alpha_{j}}\);如果乘上一个它没有的质因子 \(p_{k+1}\),那么因子个数会乘以 \(2\)。
因此由于 \(10^{18} < 2 \times 3 \times ... \times 53\),而 \(2^6 > 53\),故只有很少几次会选择乘上已经拥有的因子。因此因子数上界为 \(O(2^{15})\)(\(47\) 是第 \(15\) 个质数),常数一般在 \(10\) 以下。故可以估计约为 \(3 \times 10^5\)。故可以暴力枚举并 \(O(1)\) 判断答案。
如果有多次询问用到每一个数的所有质因子,那么可以线性筛的时候记录每个数的最小质因子,然后一直跳转。
1.11 扩展辗转相除
关于辗转相除法,可以推广到幂次、斐波那契、周期等,而一般有辗转相除就可以证明 gcd 相关的东西。
- 求 \(\gcd(a^n - 1, a^m - 1)\)。
解:假设 \(n>m\)。
相当于辗转相除。因此等于 \(a^{\gcd(n,m)}-1\)。
- 求 \(\gcd(\operatorname{Fib}_n, \operatorname{Fib}_m)\)。
解:
引理一、\(\gcd(\operatorname{Fib}_n, \operatorname{Fib}_{n+1})=1\)。
证明:可以利用 \(\gcd(n,m)=\gcd(n,m-n)\) 规约到 \(\gcd(\operatorname{Fib}_1, \operatorname{Fib}_{2})=1\)。
引理二、
考虑
因此
类似辗转相除法。
因此等于 \(\operatorname{Fib}_{\gcd(n,m)}\)。
1.12 线性空间视角看辗转相除
考虑集合 \(a_1, ..., a_n\) 能线性表出的元素集合。显然等于 \(a_1 - a_2, ..., a_n\) 能线性表出的集合,因此我们有辗转相减,那么推出有辗转相除。并且一个数减到了 \(0\) 的时候也就没有任何作用了。最后留下来的一个数就是这一个系列的单位元,可以表出的数字的集合就是 \(k\epsilon\)。可以证明这个数是 \(\gcd(a_1,...,a_n)\)。
如果要求 \(x_1a_1 + x_2a_2 + ... + x_na_n = k\) 的解怎么办?首先 \(\epsilon | k\),也就是 \(\gcd(a_1,...,a_n) | k\),然后我们考虑右边是 \(\gcd\) 的情况。考虑递归处理。如果我们有 \(x_2'a_2 + ... + x_n'a_n = \gcd(a_2,...,a_n)\),那么可以解方程 \(x_1a_1 + t \gcd(a_2,...,a_n) = \gcd(a_1,...,a_n)\),一个解就是 \((x_1, x_2't, x_3't, ..., x_n't)\)。
如果是二维平面上呢?
二维平面上向量线性空间可达问题
给定一些平面上的整数向量,求是否能给每个向量配一个非负系数,使得乘积之和可以覆盖所有整点。
\(T \le 20000, n \le 100, -100 \le x_i, y_i \le 100\)。
首先对于系数是任意实数的问题,如果有一对不共线的向量,则可以表出所有平面上的向量。
其次考虑整数系数的问题。
我们定义向量的减法了,那么我们依然有辗转相减法则正确。注意这时我们并未丢失任何可达点,只是做恒等变换而已。考虑先对 \(x\) 坐标尽量减到 \(0\),也就是前面都是 \(0\),只有最后一个可以不是 \(0\)。这样构成的向量组可以组成的点的横坐标一定被 \(x_n\) 整除。(注意不是每一个横坐标被 \(x_n\) 整除的点都能表出,不是充分条件)
这时考虑前 \(n-1\) 个 \(y\) 轴上的向量。如果它们的 \(y\) 值 \(\gcd\) 等于 \(1\),那么它们可以表出 \(y\) 轴上任意一个向量。于是加上最后一个向量显然可以表出 \(x\) 轴上的单位向量。于是所有整点都可以表出了。否则,它们无法表出 \((0, 1)\),一定不可以。
再考虑非负数系数的条件。
考虑能否将一个向量的加法可逆。(转化操作的重要思想一定要试试)
如果所有的向量均在一个半平面上(注意边界问题,这里可以是退化的三角形,因此半平面是可以有恰好等于 \(\pi\) 的),那么一定表出的全是这个半平面上的向量,显然 NO。否则,考虑某一个向量,一定能找到两个向量与其三点能够组成一个不退化的三角形。于是能找到一个向量的逆元。因此转化为了可以是负数的。
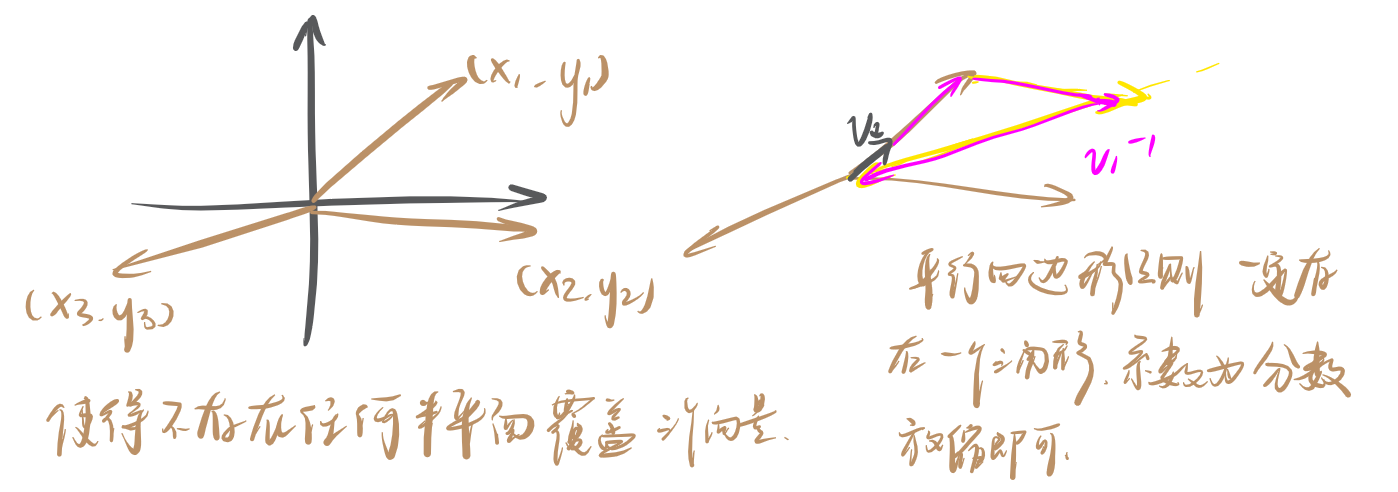
考虑一些边角料证明:首先这些向量组成三角形的系数一定是有理数(一定有一组解),这个是因为高斯消元在有理数域内封闭,并且通过几何直观证明了一定有非负数解,因此证完。其次为什么一定能找到三个向量满足条件。任意选择两个向量,则其反夹角上一定存在一个向量。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
struct vec {int x, y; } a[210];
typedef pair<vec, vec> pvv;
vec operator- (vec x, vec y) { return (vec){x.x - y.x, x.y - y.y}; }
vec operator+ (vec x, vec y) { return (vec){x.x + y.x, x.y + y.y}; }
pvv exgcd(vec x, vec y) {
if(x.x == 0) {return {x, y};}
else {
int d = y.x / x.x;
return exgcd((vec){y.x - d * x.x, y.y - d * x.y}, (vec){x.x, x.y});
}
}
pvv operator% (vec x, vec y) {
if(x.x < 0) {x.x = -x.x; x.y = -x.y;} if(y.x < 0) {y.x = -y.x; y.y = -y.y;}
if(x.x > y.x) swap(x, y);
return exgcd(x, y);
}
bool cmp(vec x, vec y) {
return atan2(x.y, x.x) < atan2(y.y, y.x);
}
const long double pi = acos(-1); //half pi
const long double eps = 1e-10;
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
// freopen("sparse.in","r",stdin);
// freopen("sparse.out","w",stdout);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int T; cin >> T;
while(T--) {
int n; cin >> n;
f(i, 1, n) {
cin >> a[i].x >> a[i].y;
}
sort(a+1,a+n+1,cmp);
bool ok = 1;
f(i, 1, n - 1) {
if(atan2(a[i + 1].y, a[i + 1].x) - atan2(a[i].y, a[i].x) >= pi - eps) {
ok = 0; break;
}
}
if(atan2(a[n].y, a[n].x) - atan2(a[1].y, a[1].x) <= pi + eps) {
ok = 0;
}
if(!ok) {
cout << "No\n"; continue;
}
else {
for(int i = 1; i <= n - 1; i ++) {
pvv res = a[i] % a[i + 1];
a[i] = res.first; a[i + 1] = res.second;
}
if(abs(a[n].x) != 1) {
cout << "No\n"; continue;
}
int gcd = 0;
f(i, 1, n - 1) {gcd = __gcd(gcd, a[i].y);}
if(abs(gcd) == 1) {
cout << "Yes\n"; continue;
}
else {
cout << "No\n"; continue;
}
}
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at h:mm
start coding at h:mm
finish debugging at h:mm
*/
如果 \(x, y\) 都做一遍使得最后的结果都是 \(1\) 可以吗?实际上不行,因为上面的结论并不必要。事实上有可能会是这样的情况:
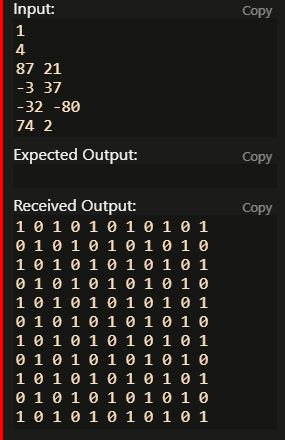
1.13 一个 trick
若 \(b|a\)(要算的东西是整数),那么有:
考虑这个东西为什么是对的:
令 \(a=(km+c)b\),那么我们需要求的是 \(c\)。
注意 \(bm\) 的范围很可能要用 int128 存。
1.14 两个 trick
对于某一个答案在 \([0, 10^{23}]\) 或者什么范围的数,模数不是质数,可能不好写,怎么办?可以采用三模合并的做法。具体地,选择三个质数,求出答案 \(\% p_1, p_2, p_3\) 的结果 \(ans_1, ans_2, ans_3\),然后使用 CRT 合并,得到一个范围在 \([0, p_1p_2p_3]\) 的数 \(t\),意义为 \(ans \bmod p_1p_2p_3 = t\)。然后如果答案范围在 \(p_1p_2p_3\) 之内,就可以这样算啦!
需要注意的是,如果答案要求 \(\bmod 2^{64}\) 之类的,那么你依然需要先 \(\mod p_1p_2p_3\) 算出真实答案,然后再去取模。否则很难调!
还有就是,快速幂的模数在这里因为是求逆元是 mod \(p\),要改。
uint64_t crt(int id) {
__int128_t res = 0;
__int128_t md[3] = {998244341, 998244353, 998244389};
__int128_t bm = md[0] * md[1] * md[2];
f(i, 0, 2) {
mod = md[i];
res += (__int128_t) ys[i][id] * (bm / md[i]) % bm * qpow(bm / md[i], md[i] - 2) % bm;
}
res %= bm;
res %= mt;
return res;
}
这里 \(ys_{i, id}\) 表示的是 \(\bmod p_i\) 的结果。
1.15 模 \(m\) 分类讨论
一个同余系统,形如:
其中 \(S_i\) 是包含于 \(m_i\) 的剩余类里面的集合,\(m_i \le 100\)。
考虑这个同余系统怎么维护解的个数。(显然 \(\bmod \mathrm{lcm}\) 是一个周期)
对于多个这样的式子,用 crt 合并它们是很困难的。(因为集合里面什么数都有,如果每一个式子的 \(m\) 的剩余类里面选一个数组合起来,有的组合有解,有的没有解)这么做的时候时间复杂度是 \(O(\mathrm{lcm} \{S_i\})\) 的。
但是有一些比较好处理的情况:如果所有 \(m_i\) 都互质,那么解的个数就是 \(\prod |S_i|\),因为任何一组组合都是合法的。然后一般情况下 \(O(\mathrm{lcm} \{S_i\}) = O(\prod S_i)\),但是如果某一个 \(S_i\) 是所有数的 \(\mathrm{lcm}\),那么会变成 \(O(S_i)\)。这是可接受的。
有一个思路很厉害:考虑定义一个 \(b\),其值为 \(2^3 \times 3^2 \times 5 \times 7(2520)\),也即 \(\sqrt {100}\) 以下所有 \(p^k\) 的乘积。我们考虑模 \(b\) 分类讨论,然后有一个性质是:假设 \(a \equiv 0 (\bmod b)\),那么 \(a \bmod q = t\) 可以改写成一个形如其 \(\cfrac{a}{2^3\times 3^2 \times 5 \times 7}\bmod (q / \gcd(b, q)) = t'\) 的式子,而这个模数是 \(1\) 或者 \(p^k\)。(当 \(t'\) 不是整数的时候,说明 \(\bmod b = 0\) 的数没有 \(\bmod q = t\) 的)例如 \(q = 2^4 \times 3\),那么 \(q / \gcd(b, q) = 2\)。如果 \(a \equiv k(\bmod b)\),那么只需维护 \(a-k\) 需要满足的限制即可。
这样所有式子都可以改写为 \(\cfrac{x}{2^3\times 3^2 \times 5 \times 7} \bmod p_i^{k_i} \in S_i'\),维护这个集合是可以做的。只需要考虑记录目前每一个质数出现的最大倍数即可,然后记录每一个 \(\bmod p_i^{maxpower_{p_i}}\) 的数是否位于 \(S\) 内。
关于 \(t'\) 怎么求:首先 \(t'\) 的最小正周期是 \(\gcd(b, q)\):
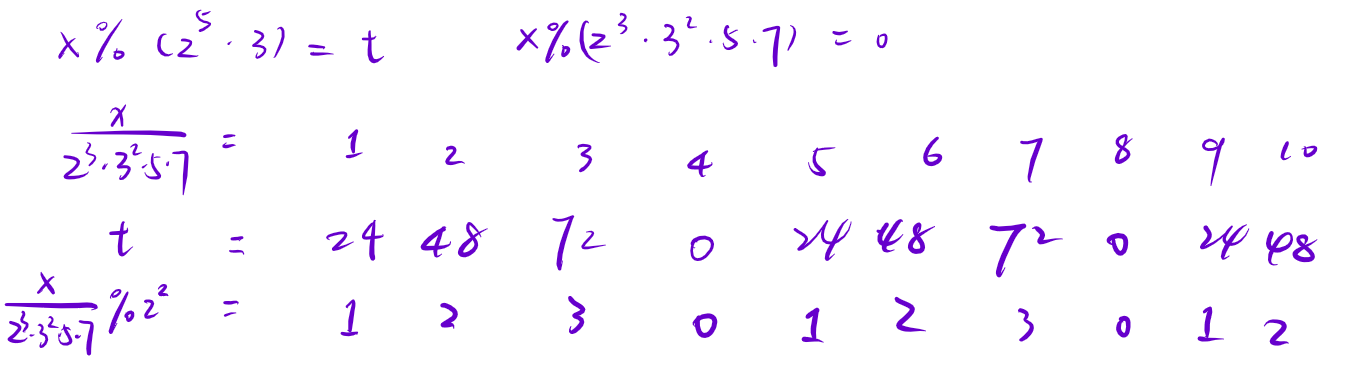
这是为什么呢?因为 \(\gcd(b, q) \times b | q\),而小于它的数不行;并且显然有 \((x + \gcd(b, q)) \times b \equiv x \times b (\bmod q)\)。所以一定有 \(t'\) 的最小正周期是 \(\gcd(b, q)\)。
但是我能不能认为 \(24, 48, 72\) 这样的话一定是 \(q / i\) 呢?是不能的。因为 \(4 \times t \equiv 0(\bmod p)\),不一定 \(t \equiv 1(\bmod p)\)。事实上 \(p = 11\) 的时候就不成立。
所以我们可以预处理:如果我们发现某个数模 \(q\) 余数是 \(t\),那么这个数除以 \(b\) 模 \(\gcd\) 为多少。时间复杂度是 \(O(100^2)\),不是瓶颈。
2 多项式的数论性质
2.1 \(p\) 次方和引理
引理:对于任意数 \(p\) 有:
\((a+b)^p \equiv a^p + b^p (\bmod p)\)
证明:
\((a+b)^p = a^p + \dbinom{p}{1} a^{p-1}b^1 +... + \dbinom{p}{p-1} a^1b^{p-1} +b^p \equiv a^p + b^p\)
loj577 简单算术
【题意】给定 \(n\) 次多项式 \(\sum \limits_{i = 0} ^ n a_i x^i\),求其 \(m\) 次幂的 \(k\) 次项系数模 \(p\),\(p\) 是质数。
多组询问,\(p\) 固定。
\(n, p \le 50, T \le 50000, m, k \le 10^{18}\)
【分析】
记多项式为 \(A\)。
运用这个定理我们可以发现 \(A^p\) 形如:
\(A[0],0,0,...,0,A[1],0,0,...,0,A[2],0,0,...,0, ..., A[n]\) 它只有 \(n\) 个有效项。
对于 \((A^p)^t,t < p\),其有 \(tn\) 个有效项。
考虑将 \(m\) 进行 \(p\) 进制分解,然后式子的答案变成了 \(\log_p m\) 个有 \(\le (p-1)n\) 个有效项的多项式相乘。
我们考虑从小到大乘还是从大到小乘。其实从小到大乘是可以做的,因为我们可以把 \(k\) 也 \(p\) 进制分解,然后假设乘到了第 \(i\) 位,我们之前乘积的有效项也只有 \(n\) 个,就是模 \(p^i\) 余数和 \(k\) 相同的项!(因为之后不可能乘上模 \(p^i\) 不为 \(0\) 的项了)
我们可以预处理 \(A^t\),\(A^{pt}\) 和它长得一模一样。时间复杂度 \(O(n^2p^2)\)。
然后考虑每一位乘积怎么做。我们有一个 \(n\) 个元素的多项式,乘上一个 \(O(pn)\) 个元素的多项式,考虑第一个多项式某一项编号为 \(*\),第二个多项式编号为 \(\#\),记 \(k\) 后 \(i-1\) 位为 \(k'\)。那么乘起来的次数是 \(* \times p^{i}+k' + \# \times p^i\)。显然要满足 \(* + \# \equiv k_i(\bmod p)\)。枚举 \(*\),有 \(O(n)\) 个数满足限制。因此一次乘积的时间复杂度 \(O(n^2)\)。
于是总复杂度为 \(O(n^2p^2 + T \log_p m n^2)\),我们发现后一部分是主要瓶颈,并且 \(p\) 越大是越好的。因此我们只需要前面不超时,可以把 \(p\) 放到 \(p^t\),最后再模 \(p\),答案不变。(因为 \(A^{p^t}\) 和 \(A^p\) 同构)
令 \(p \le 256\),可以通过。
对于组合数模质数 \(p\) 问题,当 \(n,m\) 较大,\(p\) 较小的时候(\(n \ge p\)),有可能会出现 \(n!\) 没有逆元的情况。那么怎么处理这样的情况呢?这时候需要使用卢卡斯定理。
2.2 卢卡斯定理
也有另一个形式(展开之后的):将 \(n,m\) 拆位,假设从低到高有 \(0,...,k\) 位,那么
证明:(这个部分并不是非常自然)
考虑将其视为 \([x^m](1+x)^n\)。令 \(n = kp+ r\),其中 \(r \in [0, p)\)。
利用上面的引理我们发现 \((1+x)^n = (1+x^p)^k + (1+x)^r\)。
那么 \([x^m](1+x)^n = [x^{p\times \lfloor \frac{m}{p} \rfloor}](1+x^p)^k \times [x^{m \bmod p}](1+x)^r\)。
于是有 \(\dbinom{n}{m} \equiv \dbinom{\lfloor\frac{n}{p}\rfloor}{\lfloor\frac{m}{p}\rfloor} \times \dbinom{n \bmod p}{m \bmod p}(\bmod p)\)。


