树形背包
P2014
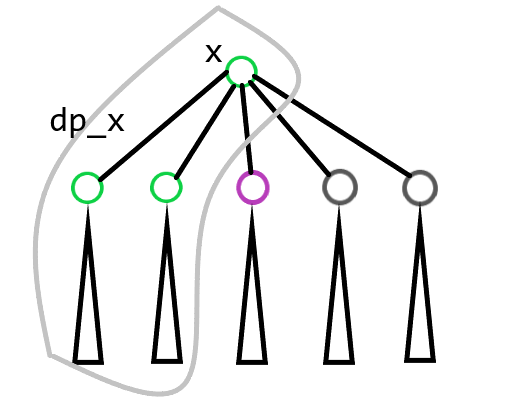
在树形 DP 的过程中,我们发现这个 DP 式子很类似背包。我们考虑在遍历子树的过程中把下图绿色部分的 \(dp\) 值和紫色部分的 \(dp\) 值合并到一起。
这样树形背包就写完了。时间复杂度 \(O(nk)\),证明见此:https://blog.csdn.net/lyd_7_29/article/details/79854245。
\(O(nk)\) 的证明繁琐,但是我们要知道它是一个平方算法,为什么呢?因为合并大小为a,b的子树复杂度是a*b,可以看成a子树内任选一点,b子树内任选一点进行匹配,不管怎么合并任意两个点只会在其lca匹配一次,所以是n^2的。
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = a; i <= b; i++)
#define mod9 998244353
#define mod1 1000000007
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
#define endl '\n'
#define cl(i, n) i.clear(), i.resize(n);
vector<int> g[310];
int dp[310][310];
int s[310];
int sz[310];
int n, m;
void dfs(int x) {
sz[x] = 1;
f(i, 0, (int)g[x].size() -1) {
dfs(g[x][i]);
for(int j = sz[x]; j >= 1; j--) {
for(int k = sz[g[x][i]]; k >= 1; k--) {
dp[x][j + k] = max(dp[x][j + k], dp[x][j] + dp[g[x][i]][k]);
}
}
sz[x] += sz[g[x][i]];
}
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
f(i, 1, n) {
int k; cin >> k;
g[k].push_back(i);
cin >> s[i];
}
memset(dp, 0xcf, sizeof(dp));
f(i ,0, n) dp[i][1] = s[i];
dfs(0);
int ans = 0;
ans= max(ans, dp[0][m+1]);
cout << ans << endl;
return 0;
}
CF1779F
【题意】
给定一棵树,点有点权 \(a_i\)。
可以进行 \(\le 2n\) 次操作,每次选定一个节点 \(i\),令其子树权值异或和为 \(x\),将其子树内所有权值都变为 \(x\)。
求使得所有点点权都变成 \(0\) 的方案,或者报告无解。
\(n \le 2 \times 10^5, a_i \le 31\)
【分析】
考虑如果一棵树的 size 是奇数,做一次操作不会改变异或和。否则,做一次操作会将子树异或和置 \(0\)。
考虑偶子树操作两次之后必定清 \(0\),因此如果 \(n\) 是偶数,一定可以直接操作两次。
否则,考虑需要将大小为奇数的树通过对若干棵偶子树进行操作(并且不能有重复操作的范围)把这个树的异或和变成 \(0\)。
也就是说,如果原树异或和为 \(xorsum\),那么要选出若干个偶子树使得其两两不交且异或和为 \(xorsum\)。
这个问题可以使用树形背包解决。记 \(dp_{i, j}\) 表示第 \(i\) 个子树内选出若干个偶子树使得其两两不交且异或和为 \(j\) 是否可行,并且记录方案。方案的大小不会太大(最小方案一定 \(\le 6\))
考虑转移过程。由于需要两两不交,要特别小心地转移。有这么些转移方式:
- 考虑一个子树 \(i\),如果它是偶子树,那么 \(dp_{i, xorsum(i)} = \{i\}\)。
- 其子树 \(j\) 上面已经可以组成的数字,\(dp_{i,k} \leftarrow dp_{j,k}\)。
- 背包过程中已经可以组成的数字 \(dp_{i,k}\),当前子树内可以组成的数字 \(dp_{j,l}\),可以组成 \(dp_{i,(k \oplus l)}\)。
首先,枚举子树的过程,第二种转移要一个一个地背上,不能先把第二种转移全背上然后再做第三种,可能会出现子树重复。
其次,第一种转移一定要是最后进行。
第三,也是最容易忽视的一个坑:\(j\) 从 \(0 \sim 31\) 枚举的时候,如果当前子树可以组成 \(j\),它是不能放在后面当 \(k\) 用的。因此需要枚举完毕再依次记录标记。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
struct node {
vector<int> son;
int sz;
int a;//xorsum
bool ok[32];
vector<int> pc[32];
node(){sz=1;f(i,0,31)ok[i]=0;}
}d[200100];
int mov[32];
void dfs(int now){
for(int i:d[now].son){
dfs(i);
d[now].a ^= d[i].a;
d[now].sz +=d[i].sz;
}
for(int i:d[now].son){
f(j, 0, 31) mov[j]=0;
f(j,0,31){
if(d[now].ok[j])continue;
else {
f(k,0,31){
if(!d[now].ok[k])continue;
else {
int tar = (k ^ j);
if(!d[i].ok[tar])continue;
else {
mov[j]=1;
for(int ppt : d[now].pc[k]) d[now].pc[j].push_back(ppt);
for(int ppt : d[i].pc[tar]) d[now].pc[j].push_back(ppt);
break;
}
}
}
}
}
f(j,0,31){
if(d[now].ok[j])continue;
if(d[i].ok[j]){
d[now].ok[j]=1;
for(int ppt : d[i].pc[j]) d[now].pc[j].push_back(ppt);
}
}
f(j, 0, 31) if(mov[j]) {d[now].ok[j] = 1;}
}
if(d[now].sz %2==0) {
if(!d[now].ok[d[now].a]) {
d[now].ok[d[now].a] = 1;
d[now].pc[d[now].a] = {now};
}
}
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n;cin>>n;
if(n%2==0){cout<<2<<endl<<1<<" "<<1<<endl;return 0;}
int xorsum = 0;
f(i,1,n){
cin>>d[i].a;
xorsum ^= d[i].a;
}
f(i,2,n){
int p;cin>>p;
d[p].son.push_back(i);
}
dfs(1);
if(xorsum == 0) {cout<<2<<endl<<1<<" "<<1<<endl;return 0;}
else if(!d[1].ok[xorsum]){cout<<-1<<endl;return 0;}
else{cout<<d[1].pc[xorsum].size()+2<<endl;for(int i:d[1].pc[xorsum])cout<<i<<" ";cout<<1<<" "<<1<<endl;}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}


