锦标赛问题

CF1717D

首先，编号之间没有区别，所以我们不妨设布置比赛的时候顺序布置，并让每场比赛中编号最小的选手获胜，如下图：

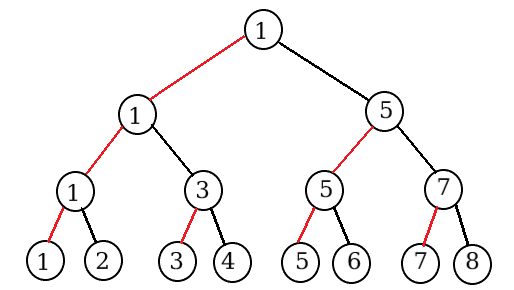
这样的比赛包含一个美妙的性质，其实是可以猜出来的：

如果把每个人的编号都 \(-1\)，变成 \(0 \sim 2^n - 1\)，然后转化为二进制，那么从右到左第 \(i\) 位是 \(0\) 就表示：这个选手所在的“\(2^i\) 个选手组成的区域”中的胜者在第 \(i+1\) 轮会赢，否则会输。

比如 \(2 = (010)_2\)，那么原来场上的 \(3\) 号选手在第一轮会赢，在第二轮会输，并且在第三轮中 \(3\) 号选手所在的 \(1 \sim 4\) 区域中胜者 \(1\) 号会赢。

这样就很容易操作了，发现把一个人保送到冠军的过程就是修改每一个 \(1\) 的位置，让他能赢。这样的话，只要 \(1\) 的个数不超过 \(k\)，那么就可以做到。

因此题意等价于：求 \(0 \sim 2^n - 1\) 里 \(\operatorname{popcount}(i) \le k\) 的 \(i\) 的个数，也就等于 \(\sum \limits_{i = 0} ^ k \C_n^i\)。这个东西直接算算就好了。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
const int mod = 1e9 + 7;
int qpow(int x, int k) {
    int ans = 1;
    while(k) {
        if(k & 1) ans = ans*x%mod;
        x=x*x%mod;
        k>>=1;
    }
    return ans;
}
int prod[100010], inv[100010];
int c(int n,int m){
    return prod[n]*inv[n-m]%mod*inv[m]%mod;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    
    int n, k; cin >> n >> k;
    if(k > n) k = n;
    prod[0]=inv[0]=1;
    f(i, 1, n) {
        prod[i]=prod[i-1]*i%mod;
        inv[i]=qpow(prod[i],mod-2);
    }
    int ans = 0;
    f(i,0,k){
        ans+=c(n,i);
        ans%=mod;
    }
    cout << ans << endl;
    time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}