背包 DP
changelog:
2022.8.29,添加了一道题目,主体还没有动工。
2022.10.24,主体开始动工。
如无特殊说明,本文中 \(v\) 表示 volume, \(w\) 表示 weight
1 经典背包模型
1.1 01 背包模型
令 \(dp_{i,j}\) 表示前 \(i\) 个物品取 \(j\) 的体积获得的最大收益。则有:
倒序枚举 \(j\) 滚掉第一维,时间复杂度 \(O(nm)\)。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
int dp[100010], v[110], w[110];
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n, k; cin >> n >> k;
f(i, 1, n) cin >> w[i] >> v[i];
f(i, 1, n) {
for(int j = k; j >= 0; j--) {
if(j - w[i] >= 0) cmax(dp[j], dp[j - w[i]] + v[i]);
}
}
int ans = 0;
f(i, 1, k) ans = max(ans, dp[i]);
cout << ans<<endl;
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
1.2 完全背包
每一件物品可选若干件。
01 背包的模板正序枚举即可。
1.3 多重背包
第 \(i\) 件物品最多选 \(c_i\) 件。
有三种做法,时间复杂度逐渐降低:
暴力拆分法
将每个物品拆分成 \(c_i\) 件,然后 01 背包。
时间复杂度 \(O(n \sum c_i)\)。
二进制拆分法
考虑物品拆成若干件之后仍可以组合成任何个数的原来的物品,并且不能组合成其他个数的物品。也就是拆成 \(2^0, 2^1, ..., 2^j, c_i - 2^{j+1} - 1\)。
时间复杂度 \(O(n \log \sum c_i)\)。
单调队列优化
单调队列可以优化的是决策区间单调移动的转移。考虑转移方程 \(dp_j \leftarrow \max \limits_{1 \le k \le c_i}\{dp_{j - k \times w_i} + k \times v_i\}\)。
虽然这样看看不出可以单调队列优化的样子,但是我们画出决策点的位置看看:
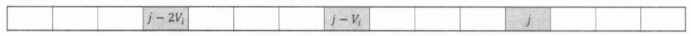
可以发现,在模 \(V_i\) 同余的意义下,不同余的状态之间不会发生任何转移:
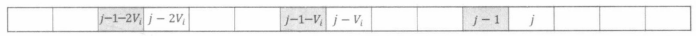
而同余的状态下,是明显的单调队列可以做的转移:

因此我们使用单调队列优化转移。
注意依然要倒序枚举!
其时间复杂度为 \(O(nm)\),也就是单层 \(i\) 循环中每个元素只会被入队和出队两次。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
int n, m;
int c[110], w[110], v[110];
int dp[100010];
int calc(int i, int u, int k) {
//i,u 是常数,calc 是单调队列排序的关键字。
return dp[u + k * v[i]] - k * w[i];
}
int q[210];
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin >> n >> m;
f(i, 1, n) cin >> c[i] >> v[i] >> w[i];
memset(dp, 0xcf, sizeof dp);
dp[0] = 0;
f(i, 1, n) {
f(u, 0, v[i] - 1) {
//模 v[i] 的余数类
int l = 1, r = 0; //单调队列,建议手写,不要用 deque
//倒序枚举
int maxp = (m - u) / v[i]; //类中的最大数的下标,下标等于数/v[i]。
//插入最初候选集合
for(int k = maxp - 1; k >= max(0ll, maxp - c[i]); k--) {
while(l <= r && calc(i, u, q[r]) <= calc(i, u, k)) r--;
q[++r] = k;
}
//倒序枚举状态
for(int p = maxp; p >= 0; p--) {
while(l <= r && q[l] > p - 1) l++;
//队列非空的话取队首决策
if(l <= r) cmax(dp[u + p * v[i]], calc(i, u, q[l]) + p * w[i]);
//插入新决策,维护队尾单调性
if(p - c[i] - 1 >= 0) {
while(l <= r && calc(i, u, q[r]) <= calc(i, u, p - c[i] - 1)) r--;
q[++r] = p - c[i] - 1;
}
}
}
}
int ans = 0;
f(i, 1, m) {
cmax(ans, dp[i]);
}
cout << ans << endl;
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
评价:二进制拆分法还是比较好写的。
Jury Compromise
题意:有 \(n\) 个人,每个人有得分 \(a_i,b_i\)。需要选择 \(m\) 个人,使得最小化 \(|\sum \limits_{j} a_j - \sum \limits_{j} b_j|\)。在此基础上,最大化 \(a_j + b_j\)。
\(n \le 200, m \le 20\)
分析:新定义“体积”和“价值”的好题。定义第 \(i\) 个人的体积为 \(a_i - b_i\)(这里不可以设为绝对值,不好转移),价值为 \(a_j + b_j\)。答案也就是 \(|a_i - b_i|\) 最小的时候 \(a_j + b_j\) 最大的一个。
由此可以看出来,\(dp\) 相当于记录了一个背包,并去重了本题意义上“等价”的东西。记录了之后我们再在背包里取用所需即可。
CF1716D
题意:给定 \(n,k\),可以从 \(0\) 开始,第一次加 \(k\) 的若干倍,第二次加 \(k+1\) 的若干倍...一直加到 \(n\)。对于 \(n=1,2,...,n\) 求方案数。
\(1 \le k \le n \le 2 \times 10^5\)
分析:是一道背包问题。对于 \(k,k+1,k+2,...,k+632\)(当 \(n=2 \times 10^5,k=1\) 时有上界 \(632\))取前一段物品,每一种物品可以取 \(1,...,\inf\) 个。是完全背包,但是需要加一个“强制跳转”的操作。
设 \(dp[i][j]\) 为只使用前 \(i\) 件物品(每一件都必须至少用一个)到达 \(j\) 的方案数。那么有如下转移:(先是像 01 背包那样强制(即覆盖之前的)往前跳一次,然后是完全背包)
dp[0]=1;
f(j,k,k+632){
for(int i = n; i >= 0; i--) {
if(i >= j) dp[i] = dp[i - j];
else dp[i] = 0;
}
f(i,1,n){
if(i-j<0)continue;
dp[i]=dp[i]+dp[i-j]; dp[i] %= mod;
ans[i] += dp[i]; ans[i] %= mod;
}
}
时间复杂度 \(O(n \sqrt n)\)(\(632 \sim \sqrt n\))
P6567 [NOI Online #3 入门组] 买表
题意:
Jimmy 到 Symbol 的手表店买手表,Jimmy 只带了 \(n\) 种钱币,第 \(i\) 种钱币的面额为 \(k_i\) 元,张数为 \(a_i\) 张。Symbol 的店里一共有 \(m\) 块手表,第 \(i\) 块手表的价格为 \(t_i\) 元。
Symbol 的手表店不能找零,所以 Jimmy 只能在凑出恰好的钱数时才能购买一块手表。现在对于店里的每块手表,Jimmy 想知道他能不能凑出恰好的钱数进行购买。
分析:
依然是先构建好背包,然后对于询问要什么给什么。
令 \(dp_i\) 表示能不能凑齐 \(i\) 元。是一个多重背包,体积就是面额。
这里采用二进制优化变成 01 背包,但是是 \(2000 \times 500000\) 的,爆炸了。没事,用个 bitset 大法。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
int cnt = 0;
int k[210], a[210], v[2010];
bitset<500010> dp;
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n, m; cin >> n >> m;
f(i, 1, n) {
cin >> k[i] >> a[i];
int pow2 = 1;
f(j, 0, 20) {
if(pow2 <= a[i] && pow2 * 2 > a[i]) {
v[++cnt] = (a[i] - pow2 + 1) * k[i];
break;
}
else {
v[++cnt] = pow2 * k[i];
pow2 *= 2;
}
}
}
dp[0] = 1;
f(i, 1, cnt) {
dp = dp | (dp << v[i]);
}
f(i, 1, m) {
int t; cin >> t;
if(dp[t]) cout << "Yes\n";
else cout << "No\n";
}
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
dp_e
题意:01 背包。
\(n \le 100, V \le 10^9, w_i \le 10^3\)
分析:
正常做是 \(O(nV)\),肯定会 T。
但是要有一个交换体积和权重的意识。毕竟体积就是权重,权重就是体积。
这道题把体积当成权重来看,把权重当成体积来看。
于是是 \(O(n^2 w_i)\) 的,能过。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
int dp[1000010];
int w[110], v[110];
int maxv = 100000;
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n, m; cin >> n >> m;
f(i, 1, n) cin >> w[i] >> v[i];
memset(dp, 0x3f, sizeof(dp));
dp[0] = 0;
f(i, 1, n) {
for(int j = maxv; j >= 0; j--){
if(j - v[i] >= 0) cmin(dp[j], dp[j - v[i]] + w[i]);
}
}
for(int j = maxv; j >= 0; j--) if(dp[j] <= m) {
cout << j << endl;
break;
}
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
2 背包优化
上次在看 He_Ren 的代码时候发现一个很重要的优化:dp 的时候记录目前背包体积和,然后只 dp 到这里,这个优化对常数的影响很大。
3 树上背包
CF440D Berland Federalization
一个大小为 \(n\) 的树,划分成若干个连通块,使得至少一个连通块包含恰好 \(k\) 个点,最小化块间的边数。
\(n,k \le 400\)
关于树上若干个连通块的问题可以考虑树形背包。
注意到只需要选出一个 \(k\) 点连通块,剩下的块就不割了。于是 \(dp_{i, j}\) 表示某几个连通块以 \(i\) 为根,\(i\) 所在的连通块大小为 \(j\),对于枚举的每一个儿子转移从 \(dp_{son, x}, dp_{i, y}\) 转移。
注意树形背包过程中 \(dp_{i, *}\) 可能会相互影响,所以比较好的方式是记录一个 \(tmp\) 数组,表示加入了这个子树之后 \(dp\) 数组的变化。待这个点全部转移完之后,再将 \(tmp\) 合并到 \(dp\) 中。
时间复杂度是 \(O(n^2)\) 的,需要记录方案,这题限制宽松可以直接 dp 里面带个 vector \(O(n^3)\) 记录,也可以使用传统的方法。
树上背包的输出方案,同样是对于每一个取用状态,判断是从哪一个状态转移来的(值等于那个状态转移过来的值)。但是问题是按照之前的记录方法,后面的会影响前面的 \(dp\) 值。应该怎么做呢?
可以换一种更好的方式记录 \(dp\) 值:\(dp'_{i,j,k}\) 表示算完 \(j\) 个儿子之后 \(dp_{i,k}\) 的值。为了保证时间复杂度,开不定长数组,那么状态数就等于原来的转移数 \(O(n^2)\)。同时这样就可以保留所有信息了。
还原的时候,考虑过程 \(\tt{getans(i,x)}\) 表示 \(dp_{i,x}\) 选的是哪 \(x\) 个点。倒序枚举儿子,注意找到一个符合条件的 \((j,r)\) 之后 \(x \rightarrow x-r\),递归到 \(\tt{getans(j,r)}\),并且 break 掉 \(j\) 的枚举。
本题转移还有其独特的一个可以学习的地方:这题记录的是连通块到外部的边数,我们可以不记录其根到父亲的那一条边,只记录子树内的边;初始时认为每个儿子都和自己断开,转移的时候如果连上一个儿子那么代价 \(-1\)。灵活设置使得转移变得简单,也是树上问题一个很重要的点。
要点:
- 一开始让 \(g\) 不包含父亲是个很好的选择。
- 注意倒序枚举。
- 注意 break。
- 注意 resize 写的对不对,不对的话可能会复杂度假掉。
vector<vector<int>> dp[401]; vector<int> g[401]; int sz[401];
int e[401][401]; vector<int> edge; pair<int, int> pre[401][401];
int ans=inf; bool vis[401]; int n, k; int lst; int anc[401];
void dfs(int now) {
sz[now]++; dp[now].resize(g[now].size() + 1); dp[now][0].resize(sz[now] + 1);
dp[now][0][1]=g[now].size(); int cnt = 0;
for(int i : g[now]){
dfs(i); dp[now][++cnt].resize(sz[now] + sz[i] + 1); fill(dp[now][cnt].begin(), dp[now][cnt].end(), inf);
f(x, 1, sz[now]) dp[now][cnt][x] = dp[now][cnt - 1][x];
f(x, 1, sz[i]) f(y, 1, sz[now])
if(dp[now][cnt][y+x] > dp[now][cnt - 1][y] + dp[i][g[i].size()][x] - 1) {
dp[now][cnt][y+x] = dp[now][cnt - 1][y] + dp[i][g[i].size()][x] - 1;
}
sz[now] += sz[i];
}
if((int)dp[now][g[now].size()].size() >= k + 1 && ans > dp[now][g[now].size()][k])
ans = dp[now][g[now].size()][k] + (now != 1), lst = now;
}
void getans(int now, int r) {
vis[now] = 1; if(r == 1) return; int cnt = g[now].size();
for(auto it = g[now].rbegin(); it != g[now].rend(); it++) {
int i = *it;
f(x, 1, sz[i]) {
if(r - x < 0 || (int)dp[now][cnt - 1].size() <= r - x) continue;
if(dp[now][cnt][r] == dp[now][cnt - 1][r - x] + dp[i][g[i].size()][x] - 1) {
getans(i, x); r -= x; break;
}
}
--cnt;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号