构造
构造题常常需要发现一些隐蔽的性质。提高观察力!
CF1670E
题目大意
给定一个 \(n = 2^p\) 个节点的树的形态,需要给每个点和每条边赋权值,一共 \(n\) 个点和 \(n-1\) 条边,权值在\([1, 2n-1]\) 里面选并且不能重复。然后钦定一个根节点。
需要使根节点到每个点和每条边的路径上的权值异或和的最大值最小\(^{*}\),求构造方案。
\(^{*}\) 比如下图,\(p=2\),根节点是权值为 \(3\) 的点:
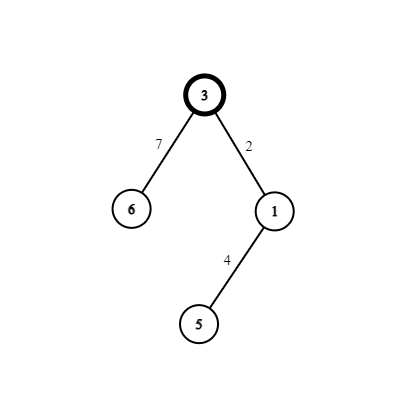
所有参与比较的异或和为:
\(3 ;\)
\(3⊕7=4;\)
\(3⊕7⊕6=2;\)
\(3⊕2=1;\)
\(3⊕2⊕1=0;\)
\(3⊕2⊕1⊕4=4;\)
\(3⊕2⊕1⊕4⊕5=1.\)
最大值为 \(4\),是该形态树的一个最优解。
题目分析
观察性质,可以看出这个最小的最大值(简记为答案)应该是 \(n = 2^p\):
由于存在 \(2^p \sim 2^{p + 1}\) 的权值并且每个权值至少贡献一次,所以当第一次碰到这类权值的时候,异或和的第 \(p+1\) 位是 \(1\),因此答案不会小于 \(2^p\)。
考虑如何构造一颗满足答案为 \(n\) 的树。
我们有如下做法:
- 任意取根节点,并将 \(n\) 作为根节点权值。
- 从根节点开始,每向下拓展一层,对于下一层的点和这两个点之间的连边做如下赋值操作:如果这一层的点权为 \(1 \sim n-1\), 那么将边权赋 \(n + k\), 下一层的点权赋 \(k\)(\(k \in [1, n - 1]\),不取重复值)
为什么此法可行?因为每一条链上的异或和都是形如
\(n\)
\(n ⊕ n+k_1 = k_1 < n\)
\(n ⊕ n+k_1 ⊕ k_1 = 0\)
\(n ⊕ n+k_1 ⊕ k_1 ⊕ k_2 = k_2 < n\)
\(n ⊕ n+k_1 ⊕ k_1 ⊕ k_2 ⊕ n+k_2 = n\)
\(n ⊕ n+k_1 ⊕ k_1 ⊕ k_2 ⊕ n+k_2 ⊕ n+k_3 = n ⊕ n+k_3 = k_3 < n\)
\(...\)
这样的东西,满足要求。
个人代码
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = a; i <= b; i++)
#define mod9 998244353
#define mod1 1000000007
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
#define endl '\n'
vector<vector<int>> g;
int cnt, n;
int node[300010], ver[300010];
map<pii, int> m;
void dfs(int x, int fa) {
f(i, 0, g[x].size() - 1) {
if(g[x][i] != fa) {
int nxt = g[x][i];
if(node[x] >= n) {
int v = m[make_pair(x, nxt)];
ver[v] = n + cnt; node[nxt] = cnt;
cnt++;
}
else {
int v = m[make_pair(x, nxt)];
ver[v] = cnt; node[nxt] = n + cnt;
cnt++;
}
dfs(nxt, x);
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
int t; cin >> t;
while(t--) {
int p; cin >> p; n = (1 << p);
g.clear(); g.resize(n + 5);
f(i, 1, n - 1) {
int u, v; cin >> u >> v; g[u].push_back(v); g[v].push_back(u);
m[make_pair(u, v)] = i; m[make_pair(v, u)] = i;
}
cnt = 1;
cout << 1 << endl;
node[1] = n;
dfs(1, 0);
f(i, 1, n) cout << node[i] << " \n"[i == n];
f(i, 1, n - 1) cout << ver[i] << " \n"[i == n - 1];
}
return 0;
}
AGC031C
【题意】
将 \(0\) ~ \(2^n-1\) 排成一个排列 \(P\) 满足:
-
\(P_1=A\)
-
\(P_{2^n}=B\)
-
\(P_i\) 与 \(P_{i+1}\) 在二进制表示下只相差 \(1\) 位。
若无满足条件的 \(P\),输出 \(\mathtt{NO}\)。
否则第一行输出 \(\mathtt{YES}\),第二行输出任意一个满足条件的序列。
【分析】
首先 \(A\) 和 \(B\) 一定要有奇数位不同。然后考虑构造方案。
考虑归纳,不同的位数为 \(k\)。\(k=1\) 时显然有解。\(k>1\) 时,考虑每次分两半,减少两位不一样的数。为了方便,我们把三位不一样的数放在最后三位,记去除最后一位之后的数为 \(A',B'\)。那么第一半我们把 \(A'\) 变成 \(A' \oplus 1\),分界线我们把最后一位变成它的相反数,第二半我们把 \(A' \oplus 1\) 变成 \(B'\)。可以发现总过程把前 \(n-1\) 位从 \(A'\) 变成 \(B'\),并且最后一位改变了,总共导致的结果是 \(A\) 变成了 \(B\)。前一半我们规约为 \(k'=1\) 的情形,后一半我们规约为 \(k'=k-2\) 的情形,都符合归纳假设。
AGC050A
【题意】
你有注意过 AtCoder 的这个部分吗?

这里的序号,是在考虑了提高任意两个页面间跳转的速度和每个页面不显示太多的选项这两个因素,并精心考虑之后选出来的。在这个问题,你需要在每个页面只有 两个链接 的前提下实现类似的功能。
Snuke 制作了一个有 \(N\) 个页面的网站,分别标号为 \(1\) 到 \(N\) 。对每个 \(i(1\le i \le N)\) ,选出两个正整数 \(a_i\) 和 \(b_i(1\le a_i \le N)\) ,把通往第 \(a_i\) 个页面和通往第 \(b_i\) 个页面的链接加入页面 \(i\) 。这个网站必须满足以下的要求:
- 你必须能够在最多点击 \(10\) 个链接后从任意的一个页面跳转到任意的另一个页面。
在这个问题的限制条件下,我们可以证明这是一定可行的。
\(N\le1000\)
【分析】
首先看到 \(10 = \log_2 1000\),会想到完全二叉树。但是叶子要往哪里连呢?很多想法都不管用。牛逼的招数来了。利用对称性。考虑 \(i \rightarrow 2i, 2i+1\),这样对于每一个点都是一棵完全二叉树。
AGC060B
【题意】
有一个 \(n\) 点 \(m\) 边的矩阵,要求给每一个格子填数。给定一个 \((1,1)\) 到 \((n,m)\) 只能向右边或者下面走的路线 \(p\),要求填的所有数字位数不超过 \(a\),并且对于所有 \((1,1)\) 到 \((n,m)\) 只能向右边或者下面走的路线 \(q\),如果 \(q=p\),那么 \(q\) 路径上点值的 \(\operatorname{xor}\) 和为 \(0\),否则不为 \(0\)。
【分析】
这种路径有一个性质,对于每一条路径,都会穿过每一条对角线各一次。因此,对某一条对角线上所有数做 \(\operatorname{xor} x\),每一条路径的异或和不变。(反思:寻找不变量?列表?)
因此考虑对 \(p\) 上每个点置 \(0\) 处理,不影响答案。
赛时也已经发现了,一对 \(\mathtt{RD}\) 之间可以交换。但是可以交换一串数,这个条件很不好搞。但是对于相邻的 \(\mathtt{RD}\),修改只会导致一个元素的交换。如果我们取一个最大的相邻集合,例如 \(\mathtt{D[DR)[DR)[DR)DD}\),例如这样:
三个 \(q\) 里面,任意一个子集都可以替换。考虑 \(p\) 里面都是 \(0\),那么三个 \(q\) 里面不能存在一个子集异或和为 \(0\)。借助线性基相关知识可以知道,\(a\ge3\)。
因此,如果我们有 \(k\) 个折线,必要条件是 \(a \ge k\)。猜想,这个也是充分条件。
证明:考虑折线的整个斜线染成 \(2^i\)。其他 “.” 都是 \(0\),如下。
两边任意折线不超过 \(k\) 种。这样我们就每一个线路至少经过一个 \(2^k\)。
再比如
怎么说呢,就牛逼!
省选计划 模拟赛 I B
【题意】
给定 \(m\) 和 \(n\),你需要求出有多少满足以下条件的整数数组 \(a_{1\sim n}\)。
- \(1 \le a_i \le m\)。
- \(a_1=1\),\(a_i<a_{i+1}(1\le i < n)\)。
- 你可以选定一个大小为 \(m/n\) 的集合 \(S\),使得对于所有 \(1\sim m\) 的正整数 \(x\),存在唯一的一对 \(1\le i\le n,j\in S\) 满足 \(a_i+j=x\)。
答案对 \(998244353\) 取模。
对于 \(n = 4, m = 12\),有以下合法的 \(a\) 数组:
- \(\{1,2,3,4\}\),此时 \(S=\{0,4,8\}\);
- \(\{1,4,7,10\}\),此时 \(S=\{0,1,2\}\);
- \(\{1,2,7,8\}\),此时 \(S=\{0,2,4\}\)。
故你应该输出 \(3\)。
【分析】
这题首先我们是观察一下,考场上发现了可能可以往子问题上化约,但是没有科学系统地思考。
dls说过,增量构造法也就是化约子问题,是很重要的思想。
先考虑长啥样。如果把 \(a_i\) 染成黑色,其他点染成白色,那么把他们分别平移(\(S\) 中的数)位,得到的东西覆盖整个 \(1 \sim m\)。
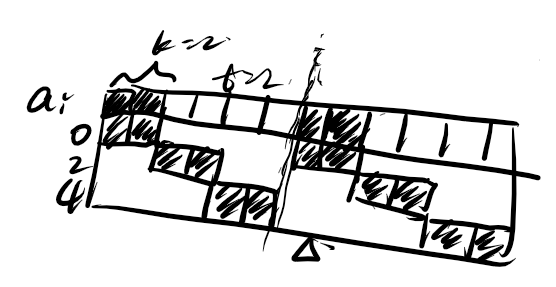
于是考虑一段连续的黑色块长度 \(k\) 是多少。这里要运用一些小 trick 或者是直觉来化约到子问题。
考虑 \(k>1\)。我们可以缩成 \((n/k,m/k)\) 的子问题,并且需要 \(k=1\):
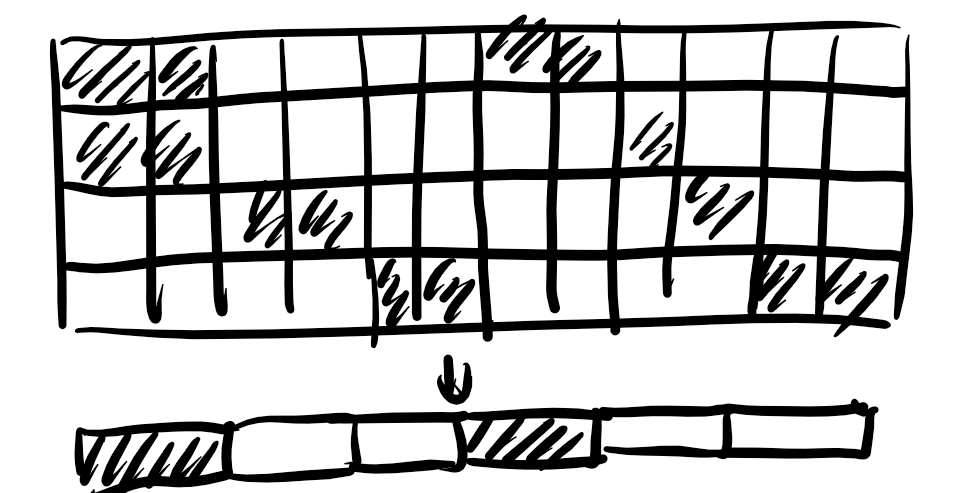
这是有理有据的,因为白色块的个数也必然是 \(k\) 的倍数。
\(k=1\),考虑一段连续白色块个数为 \(t-1 > 1\)。也可以缩成 \((n,m/t)\) 的子问题:
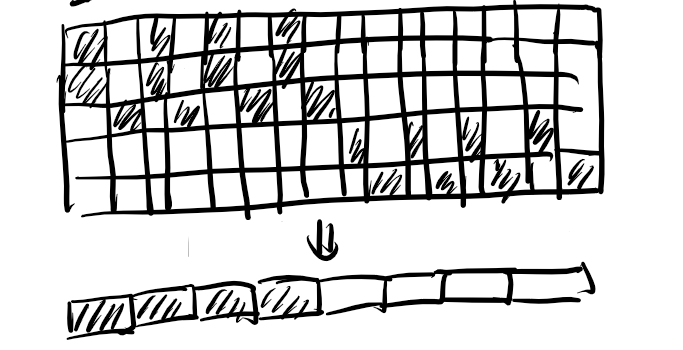
复杂度很玄学,但是感性分析一下很有必要记忆化搜索。然后就过了。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
const int mod = 998244353;
struct syz {
int x, y, z;
bool operator<(const syz opp) const {
if(x != opp.x) return x < opp.x;
if(y != opp.y) return y < opp.y;
return z < opp.z;
}
};
map<syz, int> mem;
//调不出来给我对拍!
int dp(int t, int n, int m) {
// cout << t << " " << n << " " << m << endl;
if(mem[(syz){t,n,m}]) return mem[(syz){t,n,m}];
if(n == 1) return (t == 1 ? 1 : 0);
int ans = 0;
if(t == 1) {
for(int i = n; i <= m / 2; i += n) {
if(m%i==0){
ans = (ans + dp(2, n, i)) % mod;
}
}
//m
mem[(syz){t,n,m}] = ans;
return ans;
}
else {
for(int i = 2; i * i <= n; i ++) {
if(n % i == 0) {
ans = (ans + dp(1, n / i, m / i)) % mod;
if(i * i != n) ans = (ans + dp(1, i, m / (n / i))) % mod;
}
}
ans = (ans + dp(1, 1, m / n)) % mod;
mem[(syz){t,n,m}] = ans;
return ans;
}
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n,m;cin>>n>>m;
cout<<(dp(1,n,m)+dp(2,n,m))%mod<<endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}

