分块

https://zhuanlan.zhihu.com/p/114268236

分块是一种思想，把一个整体划分为若干个小块，对整块整体处理，零散块单独处理。本文主要介绍块状数组——利用分块思想处理区间问题的一种数据结构。

块状数组把一个长度为 \(n\) 的数组划分为 \(a\) 块，每块长度为 \(\frac{n}{a}\) 。对于一次区间操作，对区间内部的整块进行整体的操作，对区间边缘的零散块单独暴力处理。（所以分块被称为“优雅的暴力”）

这里，块数既不能太少也不能太多。如果太少，区间中整块的数量会很少，我们要花费大量时间处理零散块；如果太多，又会让块的长度太短，失去整体处理的意义。一般来说，我们取块数为 \(\sqrt n\) ，这样在最坏情况下，我们要处理接近 \(\sqrt n\) 个整块，还要对长度为 \(O(\sqrt n)\) 的零散块单独处理，总时间复杂度为 \(O(\sqrt n)\) 。这是一种根号算法。

显然，分块的时间复杂度比不上线段树和树状数组这些对数级算法。但由此换来的，是更高的灵活性。与线段树不同，块状数组并不要求所维护信息满足结合律，也不需要一层层地传递标记。但它们又有相似之处，线段树是一棵高度约为 的树，而块状数组则可被看成一棵高度为3的树：

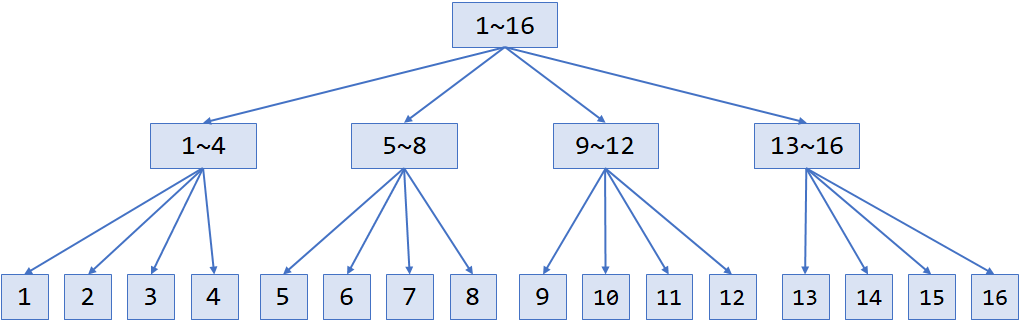
只不过，块状数组最顶层的信息不用维护。

预处理
具体地使用块状数组，我们要先划定出每个块所占据的范围：

int sq = sqrt(n);
for (int i = 1; i <= sq; ++i)
{
    st[i] = n / sq * (i - 1) + 1; // st[i]表示i号块的第一个元素的下标
    ed[i] = n / sq * i; // ed[i]表示i号块的最后一个元素的下标
}

但是，数组的长度并不一定是一个完全平方数，所以这样下来很可能会漏掉一小块，我们把它们纳入最后一块中：

ed[sq] = n;

然后，我们为每个元素确定它所归属的块：

for (int i = 1; i <= sq; ++i)
    for (int j = st[i]; j <= ed[i]; ++j)
        bel[j] = i; // 表示j号元素归属于i块

最后，如果必要，我们再预处理每个块的大小：

for (int i = 1; i <= sq; ++i)
    size[i] = ed[i] - st[i] + 1;

好了，准备工作做完了，后面的事情就很简单了。分块的代码量也许不比线段树小多少，但看起来要好理解很多，我们先来搞线段树模板题。

（洛谷P3372 【模板】线段树1）

题目描述
如题，已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 k。
求出某区间每一个数的和。

输入格式
第一行包含两个整数 n, m，分别表示该数列数字的个数和操作的总个数。
第二行包含 n 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。
接下来 m 行每行包含 3 或 4 个整数，表示一个操作，具体如下：
1 x y k：将区间 [x, y] 内每个数加上 k 。
2 x y：输出区间 [x, y] 内每个数的和。
这个题数据范围只有 ，可以用分块。我们用一个sum 数组来记录每一块的和，mark数组来做标记（注意这两者要分开，因为处理零散块时也要用到标记）。

读入和预处理数据

    int n, m; cin >> n >> m;
    f(i, 1, n) cin >> a[i];
    len = sqrt(n);
    int block_sum = (ceil)(n * 1.0 / len);
    f(i, 1, block_sum) {
        st[i] = len * (i - 1) + 1;
        en[i] = len * i;
    }
    en[block_sum] = n;
    f(i, 1, block_sum) f(j, st[i], en[i]) bl[j] = i, sum[i] += a[j];

区间修改
首先是区间修改，当x与y在同一块内时，直接暴力修改原数组和sum数组：

    if(bl[x] == bl[y]) {
        f(i, x, y) {
            a[i] += k; sum[bl[i]] += k;
        }
    }

否则，先暴力修改左右两边的零散区间：

        f(i, x, en[bl[x]]) {a[i] += k; sum[bl[i]] += k;}
        f(i, st[bl[y]], y) {a[i] += k; sum[bl[i]] += k;}

然后对中间的整块打上标记：

        f(i, bl[x] + 1, bl[y] - 1) {
            tag[i] += k;
        }

区间查询
同样地，如果左右两边在同一块，直接暴力计算区间和。

    if(bl[x] == bl[y]) {
        int ans = 0;
        f(i, x, y) ans += a[i] + tag[bl[x]];
        cout << ans << endl; 
        return;
    }

否则，暴力计算零碎块：

        int ans = 0;
        f(i, x, en[bl[x]]) ans += a[i] + tag[bl[x]];
        f(i, st[bl[y]], y) ans += a[i] + tag[bl[y]];

再处理整块：

	f(i, bl[x] + 1, bl[y] - 1) {
            ans += sum[i] + tag[i] * len;
        }

于是我们用分块A掉了线段树的模板题。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int a[100010];
int len;
int bl[100010], sum[1010], tag[1010], st[1010], en[1010];
void modify(int x, int y, int k) {
    if(bl[x] == bl[y]) {
        f(i, x, y) {
            a[i] += k; sum[bl[i]] += k;
        }
    }
    else {
        f(i, x, en[bl[x]]) {a[i] += k; sum[bl[i]] += k;}
        f(i, st[bl[y]], y) {a[i] += k; sum[bl[i]] += k;}
        f(i, bl[x] + 1, bl[y] - 1) {
            tag[i] += k;
        }
    }
}
void query(int x, int y) {
    if(bl[x] == bl[y]) {
        int ans = 0;
        f(i, x, y) ans += a[i] + tag[bl[x]];
        cout << ans << endl; 
        return;
    }
    else {
        int ans = 0;
        f(i, x, en[bl[x]]) ans += a[i] + tag[bl[x]];
        f(i, st[bl[y]], y) ans += a[i] + tag[bl[y]];
        f(i, bl[x] + 1, bl[y] - 1) {
            ans += sum[i] + tag[i] * len;
        }
        cout << ans << endl;
        return;
    }
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    int n, m; cin >> n >> m;
    f(i, 1, n) cin >> a[i];
    len = sqrt(n);
    int block_sum = (ceil)(n * 1.0 / len);
    f(i, 1, block_sum) {
        st[i] = len * (i - 1) + 1;
        en[i] = len * i;
    }
    en[block_sum] = n;
    f(i, 1, block_sum) f(j, st[i], en[i]) bl[j] = i, sum[i] += a[j];
    while(m--) {
        int typ; cin >> typ;
        if(typ == 1) {
            int x, y, k; cin >> x >> y >> k;
            modify(x, y, k);
        }
        else {
            int x, y; cin >> x >> y;
            query(x, y);
        }
    }
    time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}

对询问分块

这题还有一种做法：对询问分块。而这种分块方式也是非常精妙的：

我们单次处理 \(\sqrt n\) 个询问。
算法的核心：把输入进来的区间的 \(r\) 加一变成左开右闭区间，从而把序列切成一个一个块处理（一个块中只有第一个数是至少一个左开右闭区间的其中一个端点），也就是每个询问只是对若干个连续整块进行处理，并且块数不会超过 \(\sqrt n\)。
比如在 \([1,10]\) 的区间里面有几个询问，其左开右闭区间分别为：\([2,4),[4,7),[2,9)\)，那么这个区间分成如下几段：
\([1,1],[2,3],[4,6],[7,8],[9,10]\)，其中 \([1,1]\) 编号为 \(0\)（这里的板子里约定最前面一段没有被处理过的一大块编号为 \(0\)）
而三次询问分别是对哪几个连续整块处理？是 \(1\)；\(2\)；\(1,2,3\)。如果我们用 \(bl(i)\) 表示 \(i\) 所在块的标号，那么这个询问块区间的左右端点分别为 \(bl(l_i),bl(r_i) - 1\)。（这就是左开右闭区间的方便之处）

算法流程：

• 输入所有询问并存下来，r_i++，并对 \(l_i,r_i\) 打上 \(vis\) 标记（这个每块询问要清空），代表区间端点里有这个数。
• 遍历一遍 \(1 \sim n \color{red}{+1}\) 的整个区间，用一个变量 \(cnt\) 记录当前块的序号。对于 \(vis = 1\) 的数，cnt++，并初始化块内的一些属性。
• 遍历所有询问，这些询问都是对 \(bl(l_i),bl(r_i) - 1\) 进行操作的询问，依照题意模拟一下即可。

P3372：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int n, m; 
int a[100010], s[100010], dt[1010];
int sum[1010]; //处理块内sum
int bl[100010];  //块的编号
int typ[1010], l[1010], r[1010], k[1010];
int mp[1010];
bool vis[100010];
void solve(int m) {
    f(i, 1, m) {
        cin >> typ[i] >> l[i] >> r[i];
        r[i]++;
        if(typ[i] == 1) {
            cin >> k[i];
        }
        vis[l[i]] = vis[r[i]] = 1;
    }
    int cnt = 0;
    f(i, 1, n + 1) {
        if(vis[i]) {
            cnt++;
            mp[cnt] = i;
            dt[cnt] = 0;
            sum[cnt] = 0;
        }
        bl[i] = cnt;
        sum[bl[i]] += a[i];
    }
    f(i, 1, m) {
        if(typ[i] == 1) {
            f(j, bl[l[i]], bl[r[i]]-1)dt[j]+=k[i];
        }
        else {
            int ans = 0;
            f(j, bl[l[i]], bl[r[i]]-1)ans+=(sum[j]+dt[j]*(mp[j+1]-mp[j]));
            cout << ans << endl;
        }
    }
    f(i, 1, n) if(bl[i] != 0)a[i] += dt[bl[i]];
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    cin >> n >> m;
    int len = sqrt(m);
    f(i, 1, n) cin >> a[i];
    f(i, 1, n) s[i] = s[i - 1] + a[i];
    for(int i = 1; i <= m; i += len) {
        f(j, 1, n + 1) vis[j] = 0;
        solve(min(len, m - i + 1));
    }
    time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}

ABC265G

这个题目如果暴力做是 \(O(n^2)\) 的。

想法 1：

维护区间内的 \(0,1,2\) 分别有几个，并分治像归并排序那样求解逆序对。
这样的时间复杂度甚至是 \(O(n^2 \log n)\) 的。（当时复杂度判断失误，其实这样分治每个区间都要算一遍，而区间个数是 \(O(n)\) 级别的。）

想法 2：

直接维护区间内 \(0,1,2\) 个数和 \((0,0),(0,1),(0,2),...,(2,2)\) 每一组数对的个数，这样是可以 \(O(n \log n)\) 的，但是线段树写起来有亿点点麻烦。

#pragma GCC optimize ("O3")
#pragma GCC optimize ("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for (int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(), i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int n, q;
int a[100010];
int c[3][400010];
int t[3][400010];
int inv[3][3][400010];
void build(int now, int l, int r)
{
    if (l == r)
    {
        c[a[l]][now] = 1;
        f(i, 0, 2) t[i][now] = i;
        return;
    }
    int mid = (l + r) >> 1;
    build(now * 2, l, mid);
    build(now * 2 + 1, mid + 1, r);
    f(i, 0, 2) c[i][now] = c[i][now * 2] + c[i][now * 2 + 1];
    f(i, 0, 2) t[i][now] = i;
    f(i, 0, 2) f(j, 0, 2) inv[i][j][now] = inv[i][j][now*2]+inv[i][j][now*2+1]+c[i][now*2]*c[j][now*2+1];
}
void pushdown(int now)
{
    if (t[0][now] != 0 || t[1][now] != 1 || t[2][now] != 2)
    {
        //懒标记：这一层已经修好了，下一层还没有
        int num[3] = {0};
        int inum[3][3] = {0};
        f(i, 0, 2)
        {
            // now*2
            int cur = t[i][now * 2];
            if (cur == 0)
                t[i][now * 2] = t[0][now];
            else if (cur == 1)
                t[i][now * 2] = t[1][now];
            else
                t[i][now * 2] = t[2][now];
        }
        f(i, 0, 2)
        {
            f(j, 0, 2) {
                if (t[i][now] == j)
                    num[j] += c[i][now * 2];
            }
        }
        f(i, 0, 2) f(j, 0, 2) {
            //change to t[i][now]
            inum[t[i][now]][t[j][now]] += inv[i][j][now * 2];
        }
        f(i, 0, 2) c[i][now * 2] = num[i];
        f(i, 0, 2) f(j, 0, 2) inv[i][j][now * 2] = inum[i][j];
        f(i, 0, 2) num[i] = 0;
        f(i, 0, 2) f(j, 0, 2) inum[i][j] = 0;
        f(i, 0, 2)
        {
            // now*2
            int cur = t[i][now * 2 + 1];
            if (cur == 0)
                t[i][now * 2 + 1] = t[0][now];
            else if (cur == 1)
                t[i][now * 2 + 1] = t[1][now];
            else
                t[i][now * 2 + 1] = t[2][now];
        }
        f(i, 0, 2)
        {
            f(j, 0, 2) {
                if (t[i][now] == j)
                    num[j] += c[i][now * 2 + 1];
            }
            
        }
        f(i, 0, 2) c[i][now * 2 + 1] = num[i];
        f(i, 0, 2) f(j, 0, 2) {
            //change to t[i][now]
            inum[t[i][now]][t[j][now]] += inv[i][j][now * 2 + 1];
        }        
        f(i, 0, 2) f(j, 0, 2) inv[i][j][now * 2 + 1] = inum[i][j];        
        f(i, 0, 2) t[i][now] = i;
    }
}
void modify(int now, int l, int r, int x, int y, int ta, int tb, int tc)
{

    if (l >= x && r <= y)
    {
        int num[3] = {0};
        f(i, 0, 2)
        {
            int cur = t[i][now];
            if (cur == 0)
                t[i][now] = ta;
            else if (cur == 1)
                t[i][now] = tb;
            else
                t[i][now] = tc;
        }
        f(i, 0, 2)
        {
            if (ta == i)
                num[i] += c[0][now];
            if (tb == i)
                num[i] += c[1][now];
            if (tc == i)
                num[i] += c[2][now];
        }
        int inum[3][3] = {0};
        
        inum[ta][ta] += inv[0][0][now];
        inum[ta][tb] += inv[0][1][now];
        inum[ta][tc] += inv[0][2][now];
        inum[tb][ta] += inv[1][0][now];
        inum[tb][tb] += inv[1][1][now];
        inum[tb][tc] += inv[1][2][now];
        inum[tc][ta] += inv[2][0][now];
        inum[tc][tb] += inv[2][1][now];
        inum[tc][tc] += inv[2][2][now];
        
        f(i, 0, 2) c[i][now] = num[i];
        f(i, 0, 2) f(j, 0, 2) inv[i][j][now] = inum[i][j];

        return;
    }
    if (l > y || r < x)
        return;
    pushdown(now);
    int mid = (l + r) >> 1;
    modify(now * 2, l, mid, x, y, ta, tb, tc);
    modify(now * 2 + 1, mid + 1, r, x, y, ta, tb, tc);
    f(i, 0, 2)
    {
        c[i][now] = c[i][now * 2] + c[i][now * 2 + 1];
    }
    f(i, 0, 2) f(j, 0, 2) inv[i][j][now] = inv[i][j][now * 2] + inv[i][j][now * 2 + 1] + c[i][now*2]*c[j][now*2+1];
    return;
}

int query(int now, int l, int r, int x, int y, int op) {
    if (l >= x && r <= y)
    {
        return c[op][now];
    }
    if (l > y || r < x)
        return 0;
    pushdown(now);
    int mid = (l + r) >> 1;
    int ret = query(now * 2, l, mid, x, y, op) + query(now * 2 + 1, mid + 1, r, x, y, op);
    return ret;
}
int get(int now, int l, int r, int x, int y)
{
    //查询 [x,y] 中 op 的个数
    if (l >= x && r <= y)
    {
        return inv[2][0][now] + inv[2][1][now] + inv[1][0][now];
    }
    if (l > y || r < x)
        return 0;
    pushdown(now);
    int mid = (l + r) >> 1;
    int ret = get(now * 2, l, mid, x, y) + get(now * 2 + 1, mid + 1, r, x, y);
    f(i, 1, 2) f(j, 0, i - 1) ret += query(now * 2, l, mid, x, y, i) * query(now * 2 + 1, mid + 1, r, x, y, j);
    return ret;
}
void dfs(int now, int l, int r) {
    cout << "Vertex " << now << ", range:[" << l << ", " <<r<<"]:" << endl;
    cout << "cnt[(0,1,2)][now] = (" << c[0][now] <<", "<<c[1][now] << ", "<<c[2][now] << ")" << endl;
    cout << "tag[(0,1,2)][now] = (" << t[0][now] <<", "<<t[1][now] << ", "<<t[2][now] << ")" << endl;
    cout << "calculate the inversions:"  << endl;
    f(i, 0, 2) f(j, 0, 2) cout << "numbers of (" << i << ", " << j << ") = "<< inv[i][j][now] << endl;
    int mid = (l + r) >> 1; if(l == r) return; dfs(now * 2, l, mid); dfs(now * 2 + 1, mid + 1, r);
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    time_t start = clock();
    // think twice,code once.
    // think once,debug forever.
    cin >> n >> q;
    f(i, 1, n) cin >> a[i];
    build(1, 1, n);
    f(i, 1, q)
    {
        int typ, l, r;
        cin >> typ >> l >> r;
        if (typ == 1)
        {
            cout << get(1, 1, n, l, r) << endl;
        }
        else
        {
            int s, t, u;
            cin >> s >> t >> u;
            modify(1, 1, n, l, r, s, t, u);
        //    cout << "modify #"<<i<<", now the sgt looks like:" << endl;
        //    dfs(1, 1, n);
        }
    }
    time_t finish = clock();
    // cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}

（反正我写了大概 7k 左右，调了三天）

想法 3：
分块，块长为 \(100\)，并直接 \(O(100^3)\) 暴力做，时间复杂度 \(O(100^4)\)，比线段树好写。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int n, q; 
int a[100010];
int typ[1010], l[1010], r[1010], cg[3][1010];  //cg:query_j 让 i 变成什么
bool vis[100010];
int inv[3][3][1010];//记录第k块中前面为i，后面为j的对数
int num[3][1010];  //第j块里目前 i 的个数
int ncg[3][1010];  //现在第j块实际是 i 变成了什么
int dsc[1010], bl[100010];  //bl:第i个包含在第几块内？
void solve(int m) {
    //deal with m queries
    f(i, 1, m) {
        cin >> typ[i] >> l[i] >> r[i];
        r[i]++;
        vis[l[i]] = vis[r[i]] = 1;
        if(typ[i] == 2) {
            f(j, 0, 2) cin >> cg[j][i];
        }
    }
    //discrete
    int cnt = 0;
    f(i, 1, n + 1) {
        if(vis[i]) {
            cnt++;
            dsc[cnt] = i;
            f(j, 0, 2) ncg[j][cnt] = j;
            f(j, 0, 2) num[j][cnt] = 0;
            f(j, 0, 2) f(k, 0, 2) inv[j][k][cnt] = 0;
        }
        bl[i] = cnt;
        num[a[i]][cnt]++;
        f(j, 0, 2) if(j != a[i]) inv[j][a[i]][cnt] += num[j][cnt];
    }
    f(i, 1, m) {
        //deal with modifies
        if(typ[i] == 2) {
            f(j, bl[l[i]], bl[r[i]] - 1) {
                f(k, 0, 2) ncg[k][j] = cg[ncg[k][j]][i];
                int tmp[3] = {0};
                f(k, 0, 2) tmp[cg[k][i]] += num[k][j];
                f(k, 0, 2) num[k][j] = tmp[k];
            }
        }
        else {
            int ans = 0;
            //计算块间个数
            f(j, bl[l[i]], bl[r[i]] - 1) f(k, j + 1, bl[r[i]] - 1) {
                ans += num[2][j] * num[1][k] + num[1][j] * num[0][k] + num[2][j] * num[0][k];
            }
            //计算块内个数
            f(j, bl[l[i]], bl[r[i]] - 1) {
                f(x, 0, 2) f(y, 0, 2) {
                    if(ncg[x][j] > ncg[y][j]) {
                        ans += inv[x][y][j];
                    }
                }
            }
            cout << ans << endl;
        }
    }
    //do with real a_i
    f(i, 1, n) {
        if(bl[i] != 0) {
            a[i] = ncg[a[i]][bl[i]];
        }
    }
    return;
} 
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    cin >> n >> q;
    f(i, 1, n) cin >> a[i];
    for(int i = 1; i <= q; i += 100) {
        f(j, 1, n) vis[j] = 0;
        solve(min(100ll, (q-i+1)));
    }
    time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}