向量积
这个视频讲的很好,利用对称性揭示了向量积的本质。可以反复观看。
对于两个夹角为 \(θ\) 的 \(x-y\) 平面直角坐标系上的向量 \(\mathbf a\) 和 \(\mathbf b\),定义它们的点积为标量,数值等于 \(\mathbf {ab} \cos θ\);叉积为矢量,方向在 \(z\) 轴上,\(z\) 坐标为 \(\mathbf {ab} \sin \theta\)。
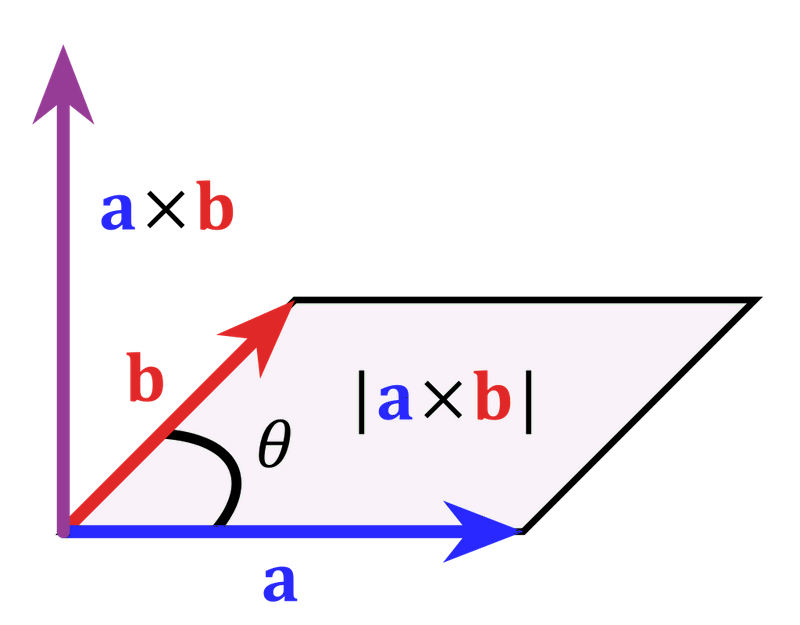
如何推出在二维坐标下两个向量的叉积公式?使用和差化积公式对这两个数值进行变形。
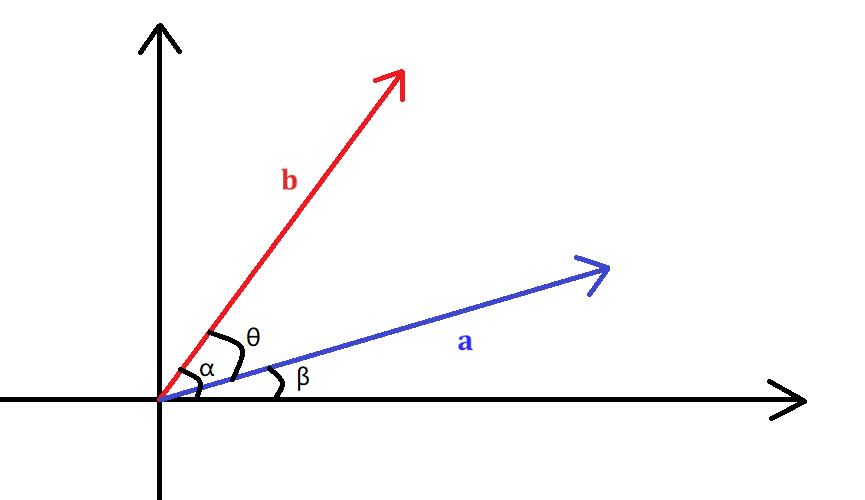
\(\mathbf {ab} \cos \theta = \mathbf {ab} \cos (\alpha - \beta) = \mathbf {ab} \cos \alpha \cos \beta + \mathbf {ab} \sin \alpha \sin \beta = A_x B_x + A_y B_y\)
\(\mathbf {ab} \sin \theta = \mathbf {ab} \sin (\alpha - \beta) = \mathbf {ab} \sin \alpha \cos \beta - \mathbf {ab} \sin \alpha \cos \beta = A_x B_y - A_y B_x\)
记忆方法:\(\cos \rightarrow x, \sin \rightarrow y\)。
叉积的性质:
-
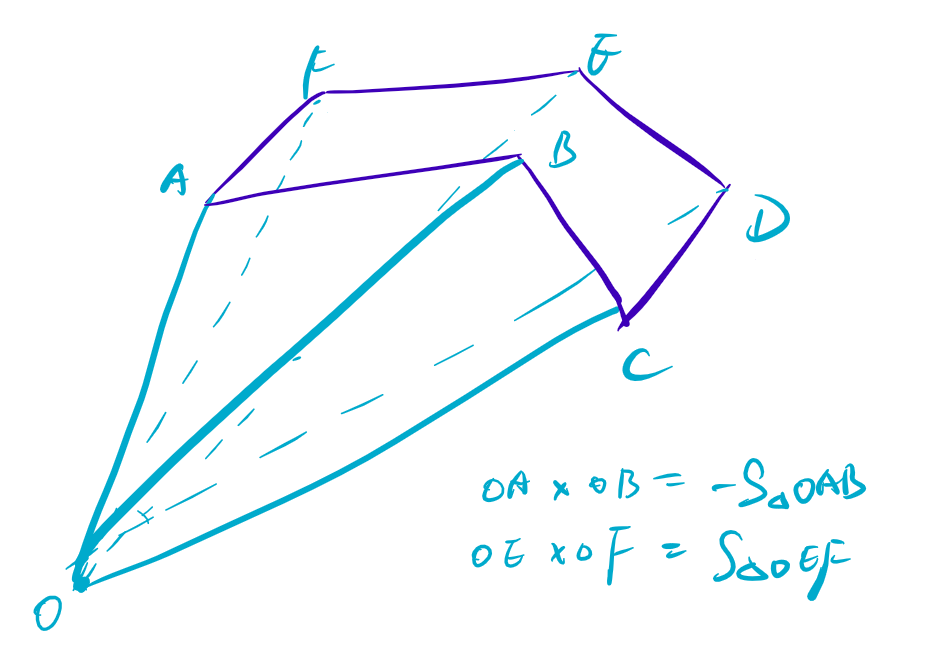
\(\mathbf{a \times b}\) 就是平行四边形的面积(前提是起点相同!)。这可以用来计算多边形的面积:对于一个多边形 \(A_0A_1...A_{n-1}\),可以计算 \(\sum \limits_{i = 1} ^ n OA_i \times OA_{i + 1 \% n}\) 并且不需要是凸多边形:
-
这里 \(\theta \in [0, \pi]\),如果是顺时针,算出来的结果是负数(也就是落在 \(z\) 轴的下方);否则是正数。顺负逆正(可以记忆为角的正负,顺是正角,逆是负角)。这可以用来判断多边形的凸性。
扩展:在三维右手系中,如果把三维旋转一下,向量本质相同,那么有:
三维坐标系中通用公式:
则
考虑高维也是类似的东西?
但其实向量叉乘只在三维和七维空间存在,考虑的二维只是 \(a_z = b_z = 0\) 的情况。
应用:判断直线是否相交
常用的方式是两个步骤:
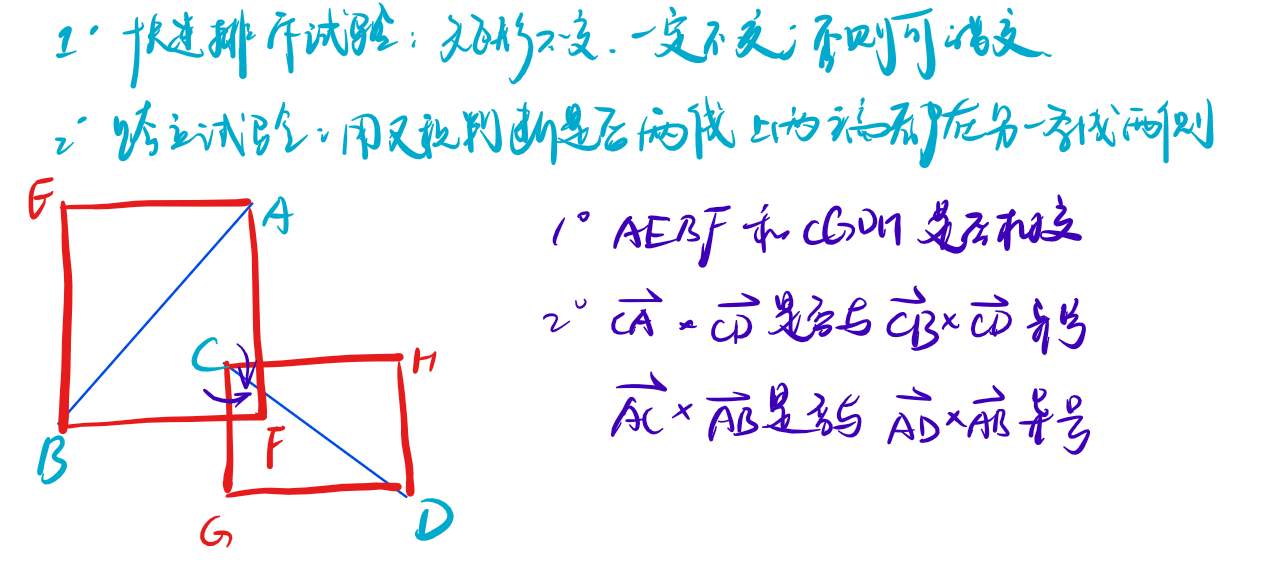
注意不同题目的需求,当叉积算出来 \(0\) 的时候可能有讨论。(快速排斥试验唯一的作用是这种情况下可以判断是否相交)
判断点是否在某个形内
将多边形按照边的顺序排好,如果在形内那么应当所有叉积都是同一个符号,类似上图多边形面积。
halt342
【题意】
小 F 居住的城市是一个四个角坐标分别为 \((0,0)\),\((0,n)\) ,\((0,m)\) ,\((n,m)\) 的矩形,其中有 \(k\) 个关键点,关键点都是整点。现在要对每个关键点分配一块地,满足每块地都处在城市内,且互不相交(指被多块地覆盖的区域面积为零)。要求每块地的形状为等腰直角三角形,对应关键点处于斜边的中点,且斜边与一条坐标轴平行、所有三角形的斜边长度相等。小 F 希望设计一个方案使得斜边的长度最大。
\(k \le 200, n, m \le 10^9\)
【分析】
这题一眼 2-sat,我们考虑变量表示某一个点是否选择某一个方向,那么列出来限制有哪些:
-
可能有一个点的一个方向选了那么另一个点的某一个方向是和它有交的,不能选。
-
可能有一个点的一个方向选了那么会超出去,不能选。
-
某一个点四个方向只能选恰好一个。
注意到前两个都是经典的 2-sat 限制,但是第三个不太好表示。我们考虑怎么表示第三个限制,赛时想到最小割,但是这样 2-sat 限制又不好表示了。那么我们思考能不能改变变量的含义。有一个 trick 是考虑记录前缀里是否有一个为真(这样是不失信息的并且可以记录前缀,但可以表示的限制是改变了一个种类的)在这个题里面不能生效。
正解是,考虑选择方向的性质。我们切成四个小三角形,每一个方向必定是对面的三角形要选一个。这样的话对面选一个是 2-sat 限制。于是可以做了。并且注意到前两个限制本质也可以拆分为这个限制。
现在问题是如何判断三角形的交的面积是否为 \(0\)。这里考虑跨立试验,如果存在一条相交的边(斜率不一样,也就是跨立试验的叉积严格异号),那么不为 \(0\)。其他的三角形面积交不为 \(0\) 情况只有重合,这只需要特判一下即可。要注意的是,不能通过判断某些边或点进行判断,如果能判断那也比这个长很多。所以使用叉积是很好的。
注意这个方法对任意三角形是适用的。
这样问题就解决了。另外我被 vector 又卡了半小时,以后记得一定不要用 vector 做所有事情,特别是在瓶颈上!是七倍常数!!!
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
struct pt {double x,y;}a[220];
inline pt operator +(pt x,pt y){return (pt){x.x+y.x, x.y+y.y};}
inline pt operator *(pt x,double y){return (pt){x.x*y, x.y*y};}
inline pt operator -(pt x,pt y){return (pt){x.x-y.x, x.y-y.y};}
pt dx[] = {{-1,-1},{1,-1},{-1,-1},{-1,1}};
pt dy[] = {{1,-1},{1,1},{-1,1},{1,1}};
vector<int> g[1620],f[1620];int n,m,k;
inline bool isin(pt x){return 0<=(x.x+x.y)/2&&n>=(x.x+x.y)/2&&0<=(x.x-x.y)/2&&m>=(x.x-x.y)/2;}
bool kuali(pair<pt,pt> x, pair<pt,pt> y){
bool tmp = 1;
//cerr << "kuali: " << x.first.x << " " << x.first.y << " " << x.second.x << " " << x.second.y << " " << y.first.x << " " << y.first.y << " " << y.second.x << " " <<y.second.y<<" "<<(x.first.x*y.first.y-x.first.y*y.first.x)*(x.first.x*y.second.y-x.first.y*y.second.x)<<" "<<(y.first.x*x.first.y-y.first.y*x.first.x)*(y.first.x*x.second.y-y.first.y*x.second.x)<<endl;
//ac, ad
double acx=y.first.x-x.first.x,acy=y.first.y-x.first.y,adx=y.second.x-x.first.x,ady=y.second.y-x.first.y,abx=x.second.x-x.first.x, aby=x.second.y-x.first.y;
if((acx * aby - acy * abx)*(adx*aby-ady*abx) >= 0) tmp=0;
// cerr<<tmp<<endl;
//ca, cb
double cax=x.first.x-y.first.x,cay=x.first.y-y.first.y,cbx=x.second.x-y.first.x,cby=x.second.y-y.first.y,cdx=y.second.x-y.first.x, cdy=y.second.y-y.first.y;
if((cax * cdy - cay * cdx)*(cbx*cdy-cby*cdx) >= 0) tmp=0;
// cerr<< "kuali: " << x.first.x << " " << x.first.y << " " << x.second.x << " " << x.second.y <<" " << y.first.x << " " << y.first.y << " " << y.second.x << " " <<y.second.y<<endl;
// cerr<<acx<<" "<<acy<<" "<<adx<<" "<<ady<<" "<<abx<<" "<<aby<<" "<<cax<<" "<<cay<<" "<<cbx<<" "<<cby<<" "<<cdx<<" "<<cdy<<" "<<acx * aby - acy * abx<<" "<<adx*aby-ady*abx <<" "<<(acx * aby - acy * abx)*(adx*aby-ady*abx)<<endl;
// cerr<<tmp<<endl;
// cout << tmp << endl;
return tmp;
}
bool jiao(double len,int i,int j,int di,int dj) {
if(a[i].x==a[j].x&&a[i].y==a[j].y&&di==dj) return 1;
pair<pt,pt> exti[4], extj[4];
exti[0]={a[i],a[i]+dx[di]*len}; exti[1]={a[i]+dx[di]*len,a[i]+dy[di]*len}; exti[2]={a[i]+dy[di]*len,a[i]};
extj[0]={a[j],a[j]+dx[dj]*len}; extj[1]={a[j]+dx[dj]*len,a[j]+dy[dj]*len}; extj[2]={a[j]+dy[dj]*len,a[j]};
// cerr << i<<endl;
// for(pair<pt,pt> x:exti) cerr << x.first.x<<" "<<x.first.y << " " << x.second.x << " "<<x.second.y<<endl;
// cerr << j<<endl;
// for(pair<pt,pt> x:extj) cerr << x.first.x<<" "<<x.first.y << " " << x.second.x << " "<<x.second.y<<endl;
//a_x b_y - a_y b_x, (x+y,x-y), (x+y, x-y)+dx[], (x+y),(x-y)+dy[]
//a_x b_y - a_y b_x, (x+y,x-y), (x+y, x-y)+dx[], (x+y),(x-y)+dy[]
f(x,0,2)f(y,0,2)if(kuali(exti[x],extj[y])) return 1;
return 0;
}
bool out(double len,int i,int di) {
return !isin(a[i]+dx[di]*len) || !isin(a[i]+dy[di]*len);
}
int num(int i, int dir, int choose) {
return dir * k + i + choose * 4 * k;
}
//每个方向,选还是不选,1600个点,方向上是 dir * k + i + (choose ? 1 : 0) * 4 * k
//调不出来给我对拍!
int cnt=0, dfn[1620], rnk[1620];bool vis[1620];int col,yse[1620];
void dfs1(int now) {
// cout << "dfs1: " << now<<endl;
vis[now]=1;//cout << "neighbors: "<<endl;
// for(int i :g[now])cout<<i<<" ";
// cout<< endl;
for(int i:g[now]){
if(!vis[i]){
dfs1(i);
}
}
dfn[now]=++cnt;rnk[cnt]=now;
}
void dfs2(int now) {
// cout << "dfs2: " << now<<endl;
yse[now]=col;
// cout << "neighbors: "<<endl;
// for(int i :f[now])cout<<i<<" ";
// cout<< endl;
for(int i:f[now]){
// cout << "haveedge" << i << endl;
if(!yse[i]){
// cout << "dfs2" << i << endl;
dfs2(i);
}
}
}
bool kosaraju() {
//dfs并且在回溯的时候赋一个cnt
//对反图进行最大标号顶点开始的dfs,然后走到的就是强连通分量。
f(i,1,8*k)vis[i]=0,yse[i]=0,cnt=0;
f(i,1,8*k){
if(!vis[i]){dfs1(i);}
}
// f(i,1,8*k) cout<< "dfn of" << i << "is " << dfn[i] << endl;
for(int i=8*k;i>=1;i--){
if(!yse[rnk[i]]){col++;dfs2(rnk[i]);}
}
// f(i,1,4*k){
// cout << i << " " << yse[i] << " " << yse[i+4*k] << endl;
// }
f(i,1,4*k)if(yse[i]==yse[i+4*k])return 0;
//cout << "return 1\n";
return 1;
}
void add(int x, int y) {
g[x].push_back(y); g[y>4*k?y-4*k:y+4*k].push_back(x>4*k?x-4*k:x+4*k);
f[y].push_back(x); f[x>4*k?x-4*k:x+4*k].push_back(y>4*k?y-4*k:y+4*k);
}
bool ok(double len) {
// cout << len << endl;
f(i,1,8*k)g[i].clear(),f[i].clear();
f(i,1,k)f(j,0,1)add(num(i,j,0),num(i,3-j,1));
f(i,1,k)f(j,0,3) {
if(out(len,i,j)) {
// cerr <<"out"<<len<<" "<<i<<" "<<j<<endl;
add(num(i,j,1),num(i,j,0));
}
}
f(i,1,k)f(j,1,k)if(i!=j)f(di,0,3)f(dj,0,3){
if(jiao(len,i,j,di,dj)){
// cerr <<"jiao"<<len<<" "<<i<<" "<<j<<" "<<di<<" "<<dj<<endl;
add(num(i,di,1),num(j,dj,0));
}
}
// f(i,1,8*k){cout<<i<<" ";for(int j:g[i]){cout<<j<<" ";} cout << endl;}
// f(i,1,8*k){cout<<i<<" ";for(int j:f[i]){cout<<j<<" ";} cout << endl;}
return kosaraju();
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
freopen("city.in","r",stdin);
freopen("city.out","w",stdout);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin>>n>>m>>k;//cout<<fixed<<setprecision(2);cerr<<fixed<<setprecision(2);
f(i,1,k){cin>>a[i].x>>a[i].y;double tx=a[i].x,ty=a[i].y;a[i].x=(tx+ty);a[i].y=(tx-ty);}
double l=0,r=1e9,eps=1e-3; //changed, need r=1e9
while(l < r-3*eps){
double mid=(l+r)/2;
// cerr << "mid=" <<mid << endl;
if(ok(mid))l=mid-eps;
else r=mid+eps;
}
cout<<fixed<<setprecision(2)<<l*2<<endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at 15:00
start coding at h:mm
finish debugging at h:mm
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号