tarjan

changelog：新建此随笔，还有一些东西未完工。
https://www.youtube.com/watch?v=TyWtx7q2D7Y

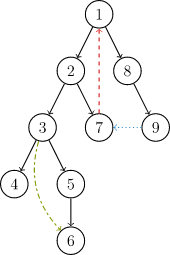
有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：

树边（tree edge）：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
反祖边（back edge）：示意图中以红色边表示（即 \(7 \rightarrow 1\)），也被叫做回边，即指向祖先结点的边。
横叉边（cross edge）：示意图中以蓝色边表示（即 \(9 \rightarrow 7\)），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。
前向边（forward edge）：示意图中以绿色边表示（即 \(3 \rightarrow 6\)），它是在搜索的时候遇到子树中的结点的时候形成的。

在 Tarjan 算法中为每个结点 维护了以下几个变量：

\(dfn_u\)：dfs 序。
\(low_i\)：由一个节点及其子树能到达的 \(dfn\) 最小节点的 \(dfn\)。这个东西是由返祖边和横叉边的存在所决定的。

割点

对于一个节点 \(u\)，如果有一个子节点 \(v\)，满足 \(low_v \ge dfn_u\)，那么删掉了 \(u\) 点，\(v\) 就没有办法再通到比 \(u\) 的 \(dfn\) 序更小的点了。
如果 \(u\) 不是根节点，那么存在比 \(u\) 的 \(dfn\) 序更小的点 \(w\)，也就找到了两个不能联通的点 \(v,w\)。那么这个点就是割点。
如果 \(u\) 是根节点，那么只要有两棵子树，那么一定是割点。所有点都满足 \(low_v \ge dfn_u\)，所以只要找到两个满足此条件的儿子即可。

桥

与之前不同的是，删掉一条边之后如果 \(v\) 还能通向 \(u\)，那么这条边也不是桥；并且如果有重边那么这条边也不是桥。
注意到这两点，我们的判定条件变成：\(low_v > dfn_u\)，并且对每条边都要考虑它是不是返祖边，使用链式前向星存图或者把相同边也存着（改天试试）都是可以的。

强连通分量

一个图中可以唯一确定地分成若干个强连通分量，其中每个强连通分量中每两个元素都可以相互连通。
将每一个强连通分量缩成一个点，可以变成一个 DAG，可以在上面进行其他操作。

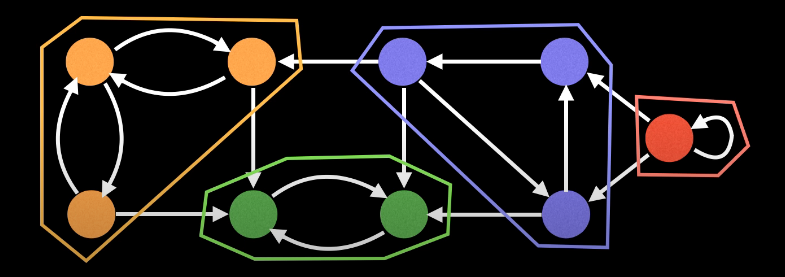
按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索，维护每个结点的 \(dfn\) 与 \(low\) 变量，且让搜索到的结点入栈。每当找到一个强连通元素，就按照该元素包含结点数目让栈中元素出栈。在搜索过程中，对于结点 \(u\) 和与其相邻的结点 \(v\)（\(v\) 不是 \(u\) 的父节点）考虑 3 种情况：

1. \(v\) 未被访问：继续对 \(v\) 进行深度搜索。在回溯过程中，用 \(low_v\) 更新 \(low_u\)。因为存在从 \(u\) 到 \(v\) 的直接路径，所以 \(v\) 能够回溯到的已经在栈中的结点，\(u\) 也一定能够回溯到。
2. \(v\) 被访问过，已经在栈中：根据 \(low\) 值的定义，用 \(low_v\) 更新 \(low_u\)。
3. \(v\) 被访问过，已不在栈中：说明 \(v\) 已搜索完毕，其所在连通分量已被处理，所以不能对其做操作。

int n, m; 
int scccnt, dfncnt;
int vis[100010], in_stack[100010];
int dfn[100010], low[100010];
vector<int> scc[100010];
int which_scc[100010];
stack<int> stk;
int rd[100010];
vector<int> g[100010];
void tarjan(int now) {
    dfn[now] = ++dfncnt, vis[now] = 1;
    low[now] = dfn[now]; in_stack[now] = 1;
    stk.push(now);
    f(i, 0, (int)g[now].size() - 1) {
        if(!vis[g[now][i]]) {
            tarjan(g[now][i]);
            low[now] = min(low[now], low[g[now][i]]);
        }
        else if(in_stack[g[now][i]]) {
            low[now] = min(low[now], low[g[now][i]]);
        } 
    }
    //判scc
    if(low[now] == dfn[now]) {
        int nowscc = ++scccnt;
        while(stk.top() != now) {
            int nxt = stk.top(); 
            stk.pop(); in_stack[nxt] = 0;
            scc[nowscc].push_back(nxt);
            which_scc[nxt] = nowscc;
        }
        stk.pop(); in_stack[now] = 0;
        scc[nowscc].push_back(now);
        which_scc[now] = nowscc;
    }
    return;
}
signed main() {
    cin >> n >> m;
    f(i, 1, m) {
        int x, y; cin >> x >> y;
        if(x != y) {
            g[x].push_back(y);
        }
    }
    f(i, 1, n) {
        if(!vis[i]) tarjan(i);
    }
}

应用：

P2002

缩点之后，变成一个 DAG，在上面找到入度为 \(0\) 的点的个数即可。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int n, m; 
int scccnt, dfncnt;
int vis[100010], in_stack[100010];
int dfn[100010], low[100010];
vector<int> scc[100010];
int which_scc[100010];
stack<int> stk;
int rd[100010];
vector<int> g[100010];
void tarjan(int now) {
    dfn[now] = ++dfncnt, vis[now] = 1;
    low[now] = dfn[now]; in_stack[now] = 1;
    stk.push(now);
    f(i, 0, (int)g[now].size() - 1) {
        if(!vis[g[now][i]]) {
            tarjan(g[now][i]);
            low[now] = min(low[now], low[g[now][i]]);
        }
        else if(in_stack[g[now][i]]) {
            low[now] = min(low[now], low[g[now][i]]);
        } 
    }
    //判scc
    if(low[now] == dfn[now]) {
        int nowscc = ++scccnt;
        while(stk.top() != now) {
            int nxt = stk.top(); 
            stk.pop(); in_stack[nxt] = 0;
            scc[nowscc].push_back(nxt);
            which_scc[nxt] = nowscc;
        }
        stk.pop(); in_stack[now] = 0;
        scc[nowscc].push_back(now);
        which_scc[now] = nowscc;
    }
    return;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    time_t start = clock();
    //think twice,code once.
    //think once,debug forever.
    cin >> n >> m;
    f(i, 1, m) {
        int x, y; cin >> x >> y;
        if(x != y) {
            g[x].push_back(y);
        }
    }
    f(i, 1, n) {
        if(!vis[i]) tarjan(i);
    }
 //   f(i, 1, n) cout << which_scc[i] << endl;
    f(i, 1, n) {
        f(j, 0, (int)g[i].size() - 1){
            if(which_scc[g[i][j]] != which_scc[i]) {
                rd[which_scc[g[i][j]]]++;
            }
        }
    }
    int ans = 0;
    f(i, 1, scccnt) {
        if(rd[i] == 0) ans++;
    }
    cout << ans << endl;
    time_t finish = clock();
    //cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
    return 0;
}