种类并查集
什么是种类并查集(也就是扩展域并查集)?今天终于搞清楚了。
并查集维护的是若干个元素之间的“关系”,那么种类并查集就是维护若干个元素的多种“关系”。
既然维护的是多种关系,那么就每一种分别维护。那么就出现了若干倍 的数组。
比如有 个人,朋友的朋友是朋友,朋友的敌人是敌人,敌人的朋友是敌人,敌人的敌人是朋友。
因为有,朋友的朋友是朋友这样的传递性,但是,也会出现,敌人的敌人是朋友,敌人的朋友是敌人这样的关系,这个时候就需要种类并查集了。
那么我们用两个长度为 的数组一起(不是分别)维护朋友关系和敌人关系。然后我们要查询的时候正常查询,维护的时候正常维护即可。
考虑怎么维护上面的关系。这里 。
如果 和 是敌人的话,考虑 。
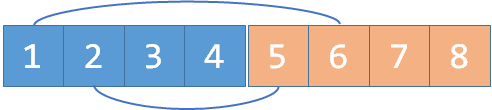
和 是敌人,我们 。
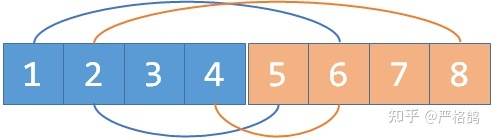
这个时候我们发现, 和 是联通的,所以 和 是朋友。
如果 和 是朋友,我们
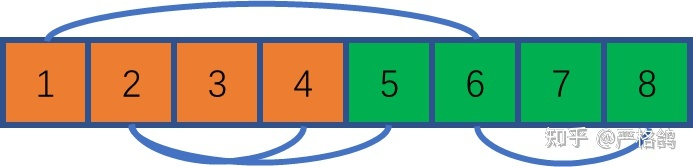
我们发现 和 联通,说明 和 是敌人。
启发:两个域并没有具体含义,里面的联通关系代表两个元素是什么关系。就像平常的并查集也是通过联通关系判断两个元素有没有亲戚关系。
P2024 食物链
二刷本题。1A。
先列出关系:
X 和 Y 同类 + Y 和 Z 同类 = X 和 Z 同类;
X 和 Y 同类 + Y 吃 Z = X 吃 Z;
X 吃 Y + Y 吃 Z = X 被 Z 吃;
...
得到一种可行的方案:
三倍 的扩展域并查集。
merge:
X 和 Y 同类:(X,Y);(X+N,Y+N);(X+2N,Y+2N)
X 吃 Y:(X,Y+N);(X+2N,Y);(X+N,Y+2N)
query:
X 和 Y 同类:(X,Y)
X 吃 Y:(X,Y+N)
X 被 Y 吃:(X,Y+2N)
发现可行。果断出手,直接拿下。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int fa[150010];
int get(int x) {
if(fa[x] == x) return x;
return fa[x] = get(fa[x]);
}
void merge(int x, int y) {
x = get(x), y = get(y);
if(x == y) return;
fa[x] = y;
}
bool same(int x, int y) {return get(x) == get(y);}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//think twice,code once.
//think once,debug forever.
int n, k; cin >> n >> k;
int ans = 0;
f(i, 1, 3*n) fa[i] = i;
f(i, 1, k) {
int t, x, y; cin >> t >> x >> y;
if(x > n || y > n){ ans++; continue;}
if(t == 2 && x == y){ ans++; continue;}
if(t == 1) {
if(same(x, y+n) || same(x, y+2*n)){ ans++; continue;}
merge(x,y);merge(x+n,y+n);merge(x+2*n,y+2*n);
}
else {
if(same(x, y+2*n) || same(x, y)){ ans++; continue;}
merge(x,y+n);merge(x+2*n,y);merge(x+n,y+2*n);
}
}
cout << ans << endl;
return 0;
}
CF1713E
题意:给定一个 的矩阵 ,矩阵里有数字。可以进行若干个如下操作:
modify(k):
for i in range [1,n]:
swap(a[i][k],a[k][i])
使得这个矩阵的字典序最小化。输出这个矩阵。
分析:赛时连贪心都没想到。字典序问题,就是要贪心,争取把当前位置搞到最优化,然后再考虑其他位置。
如果做一次操作 modify(i),那么可以将 和 交换,并且 不可能和别的位置交换了。
那么我们对于从先到后的 ,要尽可能让 。
如果一开始 ,那么就要考虑 modify(i) 或者 modify(j)。但是不能两个都做,否则没有起到交换的作用。
如果一开始 ,我们不可以让它改变。那么要么两个都不 modify,要么两个都 modify。
如果一开始 ,爱咋咋地。
并且如果给一个位置交换多次,其中的偶数次都可以相互抵消,所以只交换至多一次是足够并且最优的。
那么我们的问题变成了:进行一系列的 modify 操作,使得按顺序(优先级)满足以下条件,如果无法满足就跳过:
- 和 需要
modify其中一个。 - 和 不能只
modify其中一个。
这样的条件,类比到“朋友敌人并查集”,第一种关系相当于“敌人”关系,第二种关系相当于“朋友”关系。可以使用扩展域并查集(也叫种类并查集)。
我们先遍历一遍 ,并视情况加上“朋友”/“敌人”关系或不加关系。然后会变成两个连通块加一些孤点(因为不加关系的存在)这时候我们选择其中一个连通块(假设是标号为 的连通块)并 modify 这个连通块里所有的元素。
但是还有一个问题,如果 就是孤点不就找不到连通块了吗?这可不行。我们干脆直接让孤点全选,就避免了这个问题。
具体做法是:在开找连通块之前,如果 和 没有朋友关系也没有敌人关系,那么就让 和 存在朋友关系。(存在敌人关系也是可以的)这样做之后,整张图变成两个连通块,直接找 所在的一个即可。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int a[1010][1010];
int n;
int fa[2010];
int get(int x) {
if(fa[x] == x) return x;
return fa[x] = get(fa[x]);
}
void merge(int x, int y) {
x = get(x), y = get(y);
if(x == y) return;
fa[x] = y;
}
bool same(int x, int y) {return get(x) == get(y);}
void modify(int k) {
f(i, 1,n) swap(a[i][k], a[k][i]);
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//think twice,code once.
//think once,debug forever.
int t; cin >> t;
while(t--) {
cin >> n;
f(i, 1, n)f(j, 1, n) cin >> a[i][j];
f(i, 1,2*n) fa[i] = i;
f(i, 1, n) f(j, i + 1, n) {
if(a[i][j] > a[j][i]) {
if(same(i, j)) continue;
merge(i, j + n); merge(j, i + n);
}
else if(a[i][j] < a[j][i]){
if(same(i, j + n)) continue;
merge(i, j); merge(i + n, j + n);
}
}
f(i, 1, n) if(!same(1, i) && !same(1, i+n)) merge(1, i);
f(i, 1, n) {
if(same(i, 1)) modify(i);
}
f(i, 1,n) f(j ,1 ,n)cout << a[i][j]<<" \n"[j==n];
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具