三分法

三分法可以求出单峰函数（不一定是凸函数，可以是下面这样）的最大值（峰值），或者单谷函数的最小值（谷值）。

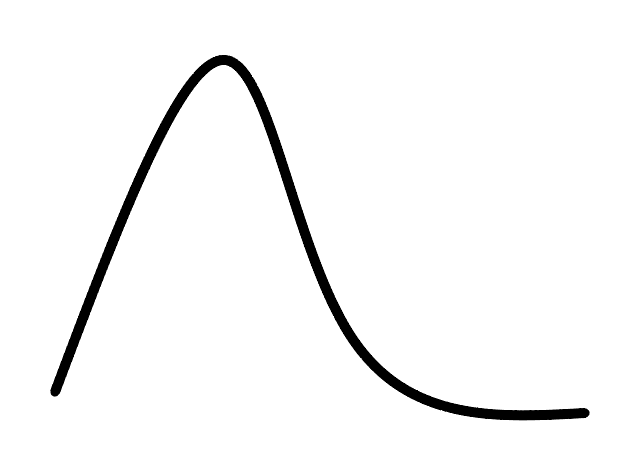
我们以单峰函数为例，在 \([l,r]\)（最小值所在范围）任取 \(l \le lmid \le rmid \le r\)，求出 \(f(lmid)\) 和 \(f(rmid)\)。

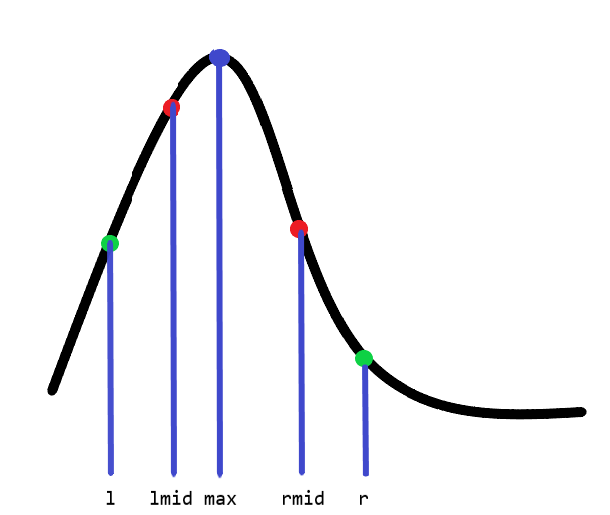
如若有 \(f(lmid) > f(rmid)\)，那么 \(rmid \sim r\) 这一段区间一定是递减的，可以缩小范围到 \((l, rmid)\)。
在实数域上三分，精度为 \(eps\) 的话，考虑什么时候结束三分。如果 \(l = r - 2 eps\)，这时刚好会出现无限循环，也就是 \(l\) 不断赋值为 \(l\)。那么我们考虑当 \(l >= r - 3eps\) 的时候结束。
例题：https://www.luogu.com.cn/problem/P3382

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
const int inf = 1e9;
int n; 
ld eps = 1e-7;
ld a[15];
ld qpow(ld x, int k) {
    ld ans = 1;
    while(k) {
        if(k&1)ans=ans*x;
        x=x*x;
        k>>=1;
    }
    return ans;
}
ld fx(ld x) {
    ld ans = 0;
    f(i, 0, n) {
        ans += qpow(x, i) * a[i];
    }
    return ans;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    //think twice,code once.
    //think once,debug forever.
    cin >> n;
    ld l, r; cin >> l >> r;
    for(int i = n; i >= 0; i--) cin >> a[i];
    while(l + 3 * eps < r) {
        ld mid = (l + r) / 2;
        ld lmid = mid - eps;
        ld rmid = mid + eps;
        if(fx(lmid) > fx(rmid)) r = rmid;
        else l = lmid;
    }
    cout << l << endl;
    return 0;
}

也可以写成 \(r \leftarrow mid, l \leftarrow mid\)，但是这样每次会掉 \(eps\) 的精度，那么我们的精度设小一点，\(0.01 \epsilon\) 差不多。

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
const int inf = 1e9;
int n; 
ld eps = 1e-7;
ld a[15];
ld qpow(ld x, int k) {
    ld ans = 1;
    while(k) {
        if(k&1)ans=ans*x;
        x=x*x;
        k>>=1;
    }
    return ans;
}
ld fx(ld x) {
    ld ans = 0;
    f(i, 0, n) {
        ans += qpow(x, i) * a[i];
    }
    return ans;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    //think twice,code once.
    //think once,debug forever.
    cin >> n;
    ld l, r; cin >> l >> r;
    for(int i = n; i >= 0; i--) cin >> a[i];
    while(l + eps < r) {
        ld mid = (l + r) / 2;
        ld lmid = mid - eps;
        ld rmid = mid + eps;
        if(fx(lmid) > fx(rmid)) r = mid;
        else l = mid;
    }
    cout << l << endl;
    return 0;
}

还有种高级的优化：优选法，但是比较难记就算了。这样写谁都会，不折腾了。