二分图博弈

1 二分图博弈

二分图博弈是一类博弈模型，他可以抽象为：给出一张二分图和起点 \(S\) ，A 与 B 轮流进行操作，每次操作只能选择与上一个被选的点相邻的点，且不能选择已经选择过的点，无法选点的人输掉。问先手是否必胜。

先给出结论：考虑二分图的所有最大匹配，如果在所有的最大匹配的方案中都包含了起点 \(S\) ，那么先手必胜，否则先手必败。

证明：

充分性：包含起点 \(S\) 时，先手每一步都只需要沿着匹配的边走，而后手的下一步一定会走到一个匹配点。因为如果走到了非匹配点 \(p_n\) ，那么假设到现在的路径是 \(S→p_1→p_2→...→p_{n−1}→p_n\) ，那么把目前已经经过的匹配 \(\{S−p_1,p_2−p_3...p_{n−2}−p_{n−1}\}\) 整体右移一下得到新的匹配 \(\{p_1−p_2,p_3−p_4...p_{n−1}−p_n\}\) ，后面的匹配不变，那么这个匹配依然是最大匹配，却不包含 \(S\) ，这与 \(S\) 是必包含点相矛盾。

必要性：不包含起点 \(S\) 时，考虑一个不包含 \(S\) 的最大匹配，先手第一步一定会走到匹配点上，否则这条边也可以加入匹配中。接下来后手可以继续沿着匹配边走，而先手一定不会走出这个匹配，因为假设走到了非匹配点 \(q_n\) ，目前的路径是 \(S→q_1→q_2→...→q_{n−1}→q_n\) ，匹配是 \(\{q_1−q_2,q_3−q_4...q_{n−2}−q_{n−1}\}\) ，那么整体右移一下得到新的匹配 \(\{q_2−q_3,q_4−q_5...q_{n−1}−q_n\}\) ，然后还可以加入一条边 \((S,q_1)\) ，形成的匹配会更大，这与最大匹配相矛盾。

综上，我们证明了这个结论。

怎么找到任意一个点是不是在二分图的所有最大匹配里呢？考虑先求出二分图的一个最大匹配。如果某个点不在最大匹配里，但是和它匹配的点可以和另一个点匹配使得匹配仍然合法，那么这个点就是非必需点。如下图：

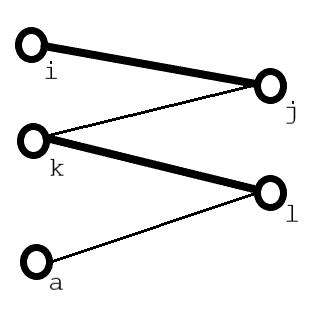
\(i\) 点连接的点是 \(j\)，\(j\) 想不和 \(i\) 配对的话可以尝试找 \(k\)。\(k\) 自己有人配，但是它的对象 \(l\) 可以找到一个没有人配的 \(a\)。因此 \(i\) 被抛弃了不是必须点。
我们对所有非匹配边从左往右连边，对所有匹配边从右往左连边，那么如果对于左边的节点 \(i\)，存在一个非匹配点 \(a\) 可以走到 \(i\) 的话，那么其不是必需点。
右边的点同理。

时间复杂度 \(O(m \sqrt n)\)。