欧拉(回)路与哈密顿(回)路
欧拉路:经过图上每条边恰好一次的路径
欧拉回路:经过图上每条边恰好一次的回路
哈密顿路:经过图上每个点恰好一次的路径(一条链)
哈密顿回路:经过图上每个点恰好一次的路径的首尾进行相接得到的回路(一个长度 \(=1\) 的点或者 \(=2\) 的环或者 \(>2\) 的简单环)
注意回路的一些对称性。
欧拉路和欧拉回路
首先删去所有孤立点。
有向图的欧拉回路
记 \(d_i\) 表示入度,\(d_o\) 表示出度。
首先考虑有向图是否存在欧拉路。
由于每条边都经过了一次,所以每一个点进出的次数是固定的,而且因为科学道理,一条路径上除了起点终点,其他点进出次数一定一样,因此首先需要有两种情况的一种出现:(必要条件)
- 有两个点分别满足 \(d_i = d_o - 1\) 和 \(d_i = d_o + 1\)。其他点满足 \(d_i = d_o\)。
- 所有点满足 \(d_i = d_o\)。
特别地,第二种情况,如果产生了欧拉路,那么也是欧拉回路。
考虑其他性质。我们先研究欧拉回路。首先因为是回路,每一个点在回路上都会到达其他所有点,所以一定是强连通图。
我们可以证明,如果有向图是强连通图并且所有点满足 \(d_i = d_o\),那么存在欧拉回路:
首先在这张图上可以找到一个环。否则是 DAG 的话会有没有入度的点,也就是孤立点。
然后如果这个环是欧拉回路,那么找到答案;否则,删掉这个环,对剩下的若干个连通块,均满足每个点度数是偶数,对这些连通块传上来的欧拉回路与这个环做加法即可找到新的欧拉回路。由于操作有限次,必然得到一个欧拉回路。
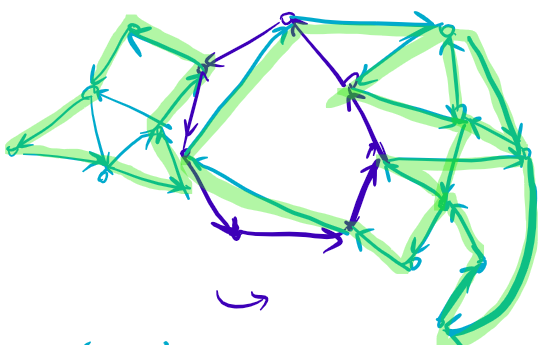
考虑构造。
有两种算法。第一种算法基于这样的思想:考虑不断删边,删边过程中不能让删掉的这条边是桥(我考虑的想法)。于是需要跑 \(m\) 遍 tarjan,时间复杂度 \(O(m^2)\)。
第二种想法(Hierholzer 希尔霍尔策 算法):和证明的思想如出一辙,考虑找到一个环,然后递归地向下可以去找到环然后拼起来。注意这个环只是要求不经过同一条边,而不是要求是简单环。
算法流程:从起点开始 dfs,考虑当前的点是 \(u\),如果存在 \((u, v)\) 没有走过,那么标记为走过并且 dfs(v)。如果不存在没走过的边,回溯并且向答案添加当前点标号。然后把整个答案数组反过来即可。

从这个例子中可以发现,我们如果找到没有没走过的边的点,这个点一定是该环的起点,然后按照反序递归回去,并顺便把删掉这个环后长在环上点上的其他部分补进去。非常精妙的思想,写起来很简单。
深究一下:为什么一直暴搜一定可以找到一个环?考虑如果某一个点是没有出边了,并且这个点还不是起点,那么这个点进去的次数是出去的次数 \(+1\),一定不会没有出边,是矛盾的。于是这个点一定是起点。而这种情况下说明已经找到了一个环。
由于我们走到某一个点的时候可以以任意顺序前往下一个点,不妨按照加入边的顺序,这时类似当前弧优化地记录目前第一个没有走到的点是哪一个,每一条边都只会记录一次。(否则时间复杂度是错的)
时间复杂度是 \(O(n + m)\)。
有向图的欧拉路和无向图的欧拉路/欧拉回路
考虑欧拉路加一条边就是欧拉回路。所以我们如果在图中加上起点到终点的边那就是欧拉回路算法了 /kk
但是还要调整边的顺序有点麻烦,能不能直接从起点开始 dfs 得到类似的东西呢?是可以的。回溯的边要么是起点,要么是终点。如果是终点(唯一的一次),把它看成向起点连的边删掉了即可。和先找欧拉回路然后删掉的做法得到的结果一样。
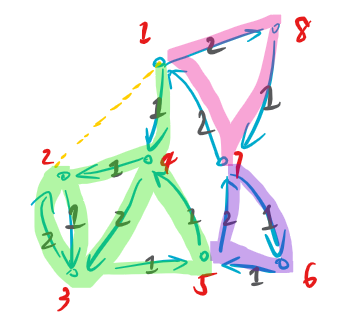
关于无向图:和有向图的区别是我们可以给每条边定向。从欧拉回路角度入手,考虑其条件是什么。首先是连通,然后是每个点的度数是偶数。一条边可以被两个中的一个端点使用。dfs 过程中,会给每一个点加一条入边和出边,所以定向的结果是正确的,因此也是可以找到欧拉回路的。(考虑有反边,那链式前向星就行了,cur 也不是没写过)对于欧拉路,我们找两个奇点中的一个做起点是一样的,因为所有边都可逆。
这样四种问题都可以在 \(O(n + m)\) 求出。
P1341
欧拉回路板子,注意四点:
- 某一个自环你直接加上即可。重边的话可以链式前向星存。
- vis 是边的 vis,这个要注意。
- 判断连通。
- 最后一定把答案反过来。
考场上大概不可以直接推出欧拉回路的来龙去脉,需背板子,这个很重要。
然后保证字典序小的欧拉回路:起点要选字典序最小的那个;对边排序,cmp 是小于号。这个实在记不住你用 ac, ab, bc 试一下就好了。但是原理是先进去的会在 v 的后方,也就是答案的前方。
#include<bits/stdc++.h>
using namespace std;
#define int long long
//use ll instead of int.
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
template <typename TYP> void cmax(TYP &x, TYP y) {if(x < y) x = y;}
template <typename TYP> void cmin(TYP &x, TYP y) {if(x > y) x = y;}
//调不出来给我对拍!
//use std::array.
vector<int> g[136];
const int m=128;
bool cmp(int x,int y){return x < y;}
vector<int> v; bool vis[136 * 136];
void hierholzer(int now) {
// cerr<<now<<endl;
for(int i:g[now]) {
if(!vis[i * m + now]) {
vis[i * m + now] = vis[now * m + i] = 1;
hierholzer(i);
}
}
v.push_back(now);
}
bool vv[2000];
void dfs(int x) {
vv[x]=1;
for(int i:g[x])if(!vv[i])dfs(i);
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
// cout << (int)'z'<<endl;
int n; cin >> n;
f(i,1,n){
char ch,hc;
cin>>ch>>hc;
g[(int)ch].push_back((int)hc);
g[(int)hc].push_back((int)ch);
}
f(i,1,m)sort(g[i].begin(),g[i].end(),cmp);
int st[200], cnt=0;
f(i,1,m){
if(g[i].size() & 1){
st[++cnt]=i;
}
}
if(cnt > 2){cout << "No Solution\n";}
else {
bool ok=1;
f(i,1,m){
if(!g[i].empty()) {
// cerr<<i<<endl;
dfs(i);
f(j,1,m)if(!vv[j]&&!g[j].empty()){
// cerr<<j<<endl;
ok=0;
}
break;
}
}
if(!ok){cout << "No Solution\n";return 0;}
int x=0;
if(cnt == 2) {x=min(st[1],st[2]);}
else {
f(i,1,m)if(!g[i].empty()){x=i; break;}
}
hierholzer(x);
// for(int i:v)
for(auto i=v.rbegin();i!=v.rend();i++) cout << (char)*i;
cout<<endl;
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/4/6
start thinking at 14:00
start coding at 14:05
finish debugging at 14:34
*/
哈密顿路和哈密顿回路
对于有向图和无向图,这类问题都是 NP-complete 的。我们有 \(O(2^n n)\) 的判定和寻找所有哈密顿路的方法:状压 dp。考虑 \(dp_{S, i}\) 表示已经走过了 \(S\) 集合,最后一个到达 \(i\),可行不可行。转移是枚举 \(i\) 邻域上的不在 \(S\) 内的点。这是 \(O(2^n n^2)\) 的。我们考虑把 \(dp_S\) 这个数组压成整数,然后枚举下一个点 \(j\),显然其反邻域(也就是什么点能到达它,如果无向图那么就是邻域)上若有点 \(i\) 满足 \(dp_{S, i} = 1\) 那么 \(dp_{S \cup j, j} = 1\)。这个就是把反邻域和数组拿来与一下就好了。
CF1804E
给定一张无向图,给每个点设置一个 \(next(next \neq i)\),目的是让每一组点对 \((i,j)\) 都满足如下条件:
- 从 \(i\) 出发,一直走 \(next\),直到 \(j\) 离这个点距离 \(\le 1\)。
首先我们发现对于一个点生成子图上的哈密顿回路,我们会在里面绕圈子。这样的话,需要有一个哈密顿回路,使得所有点到其的距离 \(\le 1\)。如果找不到这样的哈密顿回路,那么不能走环,于是变成了单向路程显然不行。
那么问题转化为了求所有生成子图上的哈密顿回路。这个其实也可以 \(O(n 2^n)\)。
朴素想法是,枚举起点,然后跑 dp,顺便检查有没有哪个点连到起点。这样是 \(O(n^2 2^n)\) 的(带上前面的优化)
也有一种 \(O(n^2 2^n)\) 的方式是不枚举起点,而是 \(dp_{S, i}\) 是一个 int20,表示这个情况下起点的集合。
这里说的 \(O(n 2^n)\) 做法是运用了回路的对称性做到的。由于每个起点都是一样的,我们不妨钦定每一个集合里最大的那个数是起点。然后我们枚举起点,时间复杂度变为 \(\sum \limits_{i = 1}^{n} O(i 2^i) \le O(n \sum 2^i) = O(n 2^n)\)。
图的平方上的哈密顿回路
对于一张图 \(G\),定义其 \(k\) 次方是一张图 \(G^k\),其点集是 \(G\) 的点集,对于 \(i \neq j\),\(i,j\) 有边当且仅当 \(G\) 上 \(i,j\) 之间的距离小于等于 \(k\)。或者说,一次可以跳到距离为 \(\le k\) 的位置。
显然对于一张图,高次方边集包含低次方边集。
对于一棵树,其平方上找一条哈密顿回路/从 \(1\) 到 \(n\) 的哈密顿路的算法是线性的。
下面介绍这个方法。
首先给出一些定义。
\(T_2\):形如这样的一个树。
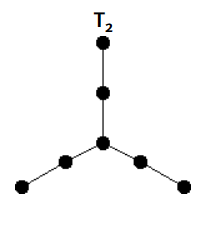
毛毛虫:一棵树,其不含有 \(T_2\)。这个定义等价于,去掉这棵树上的所有叶子之后剩下一条链。
\(\mathbf{Lemma}.\) 一棵树存在哈密顿回路当且仅当其是一个毛毛虫。
证明就是分类讨论讨论,比较繁琐,但是你首先可以写写画画一下发现 \(T_2\) 上没有哈密顿回路。然后在上面加一些叶子就更没有了。
对于毛毛虫,我们考虑怎么找它的哈密顿回路。对于一条链我们能想到这么做:

那么不难想到对于毛毛虫可以直接黑白染色一下就好了。
另外这样的话,我们的最后一个点落在了和初始位置相邻的点,这是很大的利好!
注意哈密顿回路有轮换对称性质,所以你可以认为是任意一个节点开始,然后可以停在和其相邻的位置。
这就是对于树的平方的哈密顿回路存在性的结论。下面继续探究对于树的平方,从 \(1\) 到 \(n\) 的哈密顿路的存在性。
首先我们想到利用上述的性质,尝试构造一个像样的方法。
我们考虑能不能走过 \(1\) 到 \(n\) 在树上的路径,然后在走的过程中顺便把其旁边的子树走了。
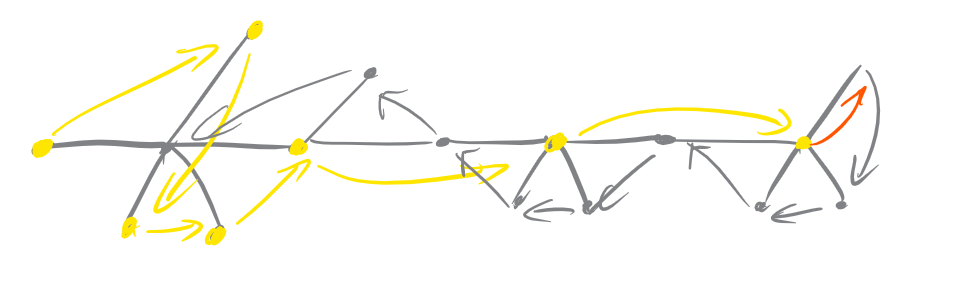
大致思路是这样的:令 \(1\) 到 \(n\) 的树上路径 \(u_0 = 1, u_1, u_2, ..., u_k = n\),然后你走 \(u_0, u_1\) 的邻点,\(u_1,u_2\) 的邻点 ... 走到 \(u_k\)。这种情况在 \(u_1, ..., u_k\) 都只有一个子树是毛毛虫的时候存在。(子树,指的是路径外的所有子树,如下图圈出了白点的三个子树)
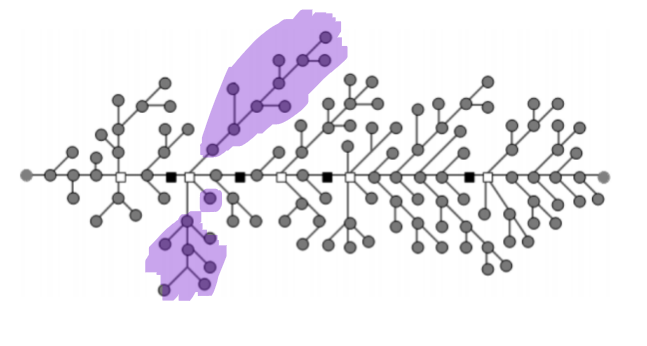
这个结构的特点是可以走到 \(u_i\) 的邻点,把它的子树走完,然后走回 \(u_i\)。但是注意只有一个点的毛毛虫性质要比这个好一点,它可以停在原地(否则必须走到其相邻点然后返回 \(u_i\))。我们把一个点的毛毛虫叫做平凡毛毛虫,因为如果有这类点,其和其他毛毛虫子树组合在一起的时候可以先把这类点走完,然后进入非平凡子树,这类点对于先走入子树再走入 \(u_i\) 的路线没有任何影响。
不妨看看如果子树变多了是什么情况。如果子树有两个非平凡毛毛虫怎么办,那只能是走一个,然后走到 \(u_i\),然后走到距离 \(u_i\) \(2\) 的点,然后走完一遍再走到 \(u_i\) 的邻点。注意这时候我们不能在 \(u_i\) 位置停留了,而是必须结束在 \(u_i\) 的相邻点位置。
如果子树有 \(\ge 3\) 个非平凡毛毛虫,显然是走不出去了。
那么这样就会有一个后遗症:后面的点只能从 \(u_i\) 进去。这时候如果来一个没有子树的点,那么会解除这个后遗症。如果来一个有一个非平凡毛毛虫子树的点,那么维持后遗症。如果走到有两个非平凡毛毛虫子树的点,那么就寄了。
我们将 \(1 \sim n\) 的路径上所有点分成四类:
A 类点:没有子树的点。
B 类点:有子树,并且有一个或零个非平凡毛毛虫子树的点。
C 类点:有两个非平凡毛毛虫子树的点。
寄点:有不是毛毛虫的子树,或者三个以上非平凡毛毛虫子树的点。
对于这条路径,需要满足以下几个条件,\(1\) 到 \(n\) 才有按刚刚思想分层走的哈密顿回路:
- 没有寄点。
- 首尾不能是 C 类点。
- 两个 C 类点中间必须有 \(\ge 1\) 个 A 类点。
例如这张图:
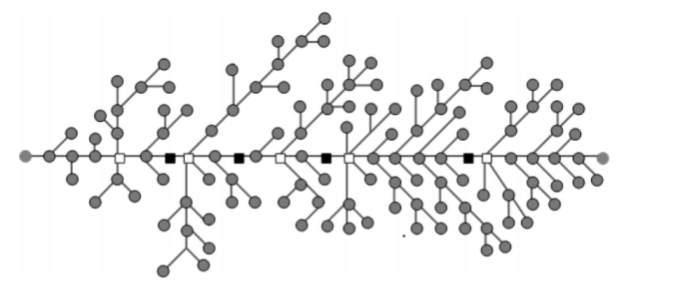
用灰色标出了 B 类点,白色标出了 C 类点,黑色标出了 A 类点。
构造是好构造的。
这个条件也是充要条件。这个我不会证明。

