最大流与二分图匹配
1 最大流问题
1.1 基本概念
原网络：不存在反向边（这是一种简化的理解方式，比较严谨的理解方式是对任意两个点定义的一个二元函数 \(f(u, v) \rightarrow R\)，满足 \(f(u, v) \le c(u, v)\)，两个方向中其中一个的 \(c\) 是 \(0\)）。
残量网络：对某个可行流 \(f\) 的残量网络为 \(G_f\)，存在反向边。
最大流问题：找最大可行流。
两个构成要素：
流量守恒：经过一个点（除了源点和汇点之外）的流量定义为从这个点流出的流量减去流入这个点的流量，它需要为 \(0\)。
容量限制：流过一条边的流量必须在 \(0 \sim c_{edge}\) 范围内。
割：将网络流的点集分为两个部分 \(S\) 和 \(T\)，源点在第一部分，汇点在第二部分。其划分结果即为一个割。
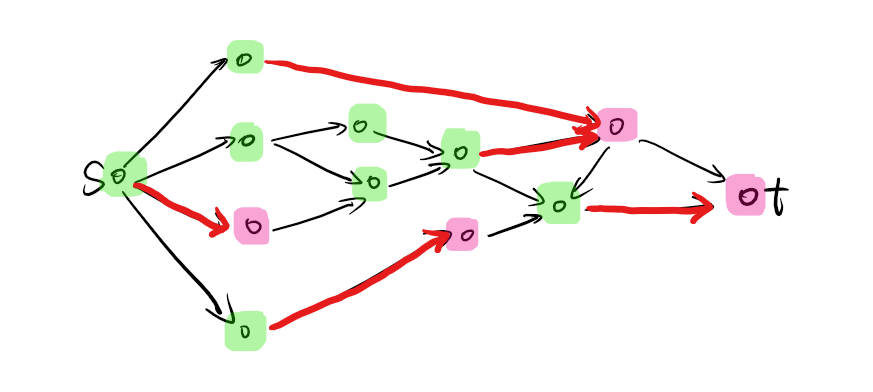
割的容量：所有从 \(S\) 连向 \(T\) 的边的容量之和。
如图所示即为一个割，标出了 \(S\)，\(T\) 以及算在割的容量里面的边。
有 \(2^{n-2}\) 种割。每一个从 \(S\) 流向 \(T\) 的流都会至少流经一条割边（中值定理）。
1.2 割的一些性质
最大流最小割定理：最大可行流流量等于最小割容量。
这个东西画图之后很直观理解：如果在最大流的每一个瓶颈上面画一个割边的话，那么该割容量就等于最大流流量；如果不是瓶颈，那么割容量会更大；如果是一个流被算了好多次，那么割容量也会更大；如果没有流满，那么流量会变小。
还有一个支持找最大流的重要定理：增广路定理，内容是最大流与残量网络没有增广路等价。
以下给出两个结论的证明：
如下三个条件知一推二：
- 可行流 \(f\) 是原图 \(G\) 的最大流。
- \(f\) 的残量网络没有增广路。
- 存在一个割 \((S,T)\) 使得 \(|f| = c(S, T)\)。
证明：
1 -> 2. 反证法，正向很好证明。
3 -> 1. 容易证明任意一个可行流流量 \(\le\) 任意一个割容量。也很好证明。
2 -> 3. 从起点开始经过残量网络中满流边 BFS 得到的连通块设为 \(S\) 即可。
因此我们证明了两个重要的结论。没有增广路就是最大流也不难理解，其本质是因为残量网络的存在使得如果有更大的流 \(f'\) 一定存在 \(f' - f\) 这个流。
其他割性质：
-
如果某一个边是最小割的割边，它一定是满流边/关键边，那么其满足关键边的性质，把若干条边串联之后这些边最多会割一条。
-
建图的时候不让割某条边，可以怎么做：从其起点向终点连一条容量 inf 的边，那么割这条边的话还需要割新加入边，否则割这条边没有意义，所以这条边不会割掉。
-
依据最大流建立的最小割，满足 \(S\) 到 \(T\) 的任何一条路径上有且仅有一条割边。（这是集合划分模型的一个前置定理）
1.3 FF 增广路算法
增广路：一条从源点到汇点的路，使得流这一条路可以使流量增加。
我们通过不断寻找增广路，并对其进行增广、加反向边直到不存在增广路，来寻找最大流。（最大流最小割定理）
于是我们有了暴力的算法：FF 增广路算法。该算法每次 DFS 寻找增广路，并对增广到的路线进行更新流量。注意这些算法中存图存的都是残量网络，有反向边的；存的边权是容量，不是流量。流量也就是增广路上边最大流量的最小值，可以边增广边记录。建反边，回溯即可。
建反边：链式前向星存图，一次存两条边，每次取成对异或变换即可。
时间复杂度：设最大流为 \(f\)。则最多有 \(f\) 次 DFS 操作。\(O(fE)\)。
1.4 EK 增广路算法
发现上一个时间复杂度里有 \(f\)，考虑消除之。原因是因为 FF 算法太死脑筋了，非要等现在节点水灌满了，才会灌其他的（明明有一个更大的水管不灌）。
考虑将 DFS 换成 BFS，时间复杂度 \(O(min(Vf, VE^2))\)。（这个复杂度很松，用下面的板子一般来说可以跑 \(1000 \sim 10000\) 的 \(n\)。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int cnt = 0;
int n,m,s,t;
int head[1010],nxt[20010],mxf[20010],to[20010],flow[1010],lst[1010];
void add(int u, int v, int w){
nxt[cnt]=head[u];to[cnt]=v;mxf[cnt]=w;head[u]=cnt;
++cnt;
}
bool bfs(){
queue<int> q;
memset(flow,0x3f,sizeof(flow)); memset(lst,-1,sizeof(lst));
q.push(s);
while(!q.empty()){
int u=q.front();q.pop(); if(u == t) break;
for(int i = head[u]; i != -1; i = nxt[i]) {
int v = to[i],w=mxf[i];
if(w>0&&v!=s&&lst[v]==-1){
flow[v]=min(flow[u],w); lst[v]=(i^1); q.push(v);
}
}
}
return (lst[t] != -1);
}
int ek(){
int maxflow = 0;
while(bfs()){
maxflow += flow[t];
for(int i = lst[t]; i != -1; i = lst[to[i]]) {
mxf[i] += flow[t]; mxf[(i ^ 1)] -= flow[t];
}
}
return maxflow;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//think twice,code once.
//think once,debug forever.
cin >> n >> m >> s >> t; f(i,1,n)memset(head,-1,sizeof(head));
f(i,1,m) {int u,v,w;cin>>u>>v>>w;add(u,v,w);add(v,u,0);}
cout<<ek()<<endl;
return 0;
}
测试：\(n=1000,m=10000\) 只跑了 \(88ms\)。
实现的时候可以改成使用 vector 存边的标号，会快一些，然后仔细一点最好不要把 to[id] 和 id 写错啥的，很难调。
1.5 Dinic 算法
可以进一步优化常数。
Dinic 算法的本质是爆搜，每次不只是搜一条路径，而是把一个残量网络中所有增广路径一起搜出来。但是可能会出现绕远路/绕环的现象，怎么办呢？我们对图跑一遍 BFS，处理出每个点和源点的距离，在搜的时候只从前一层往后一层搜。
（如果你知道咖啡店在你的东侧，你只会向东边的方向走才能尽快到达）
具体而言，这个层数是 BFS 树上的层数。BFS 的时候，是不是每个点只会经过一次？这一次的层数也就是它在 BFS 树上的层数。
这个层数建立之后，显然有一个性质，层数为 \(i\) 的点只会连向层数为 \(\le i + 1\) 的点（这点和 DFS 树不一样）。并且如果有向汇点的通路，一定有至少一条边连向层数为 \(i+1\) 的点。我们把这些边构成的导出子图，作为这次扩展的域。
然后在图上 DFS，不断寻找增广路（只需要有边权就行，不要求最大）直到没有为止。然后进行下一次 BFS。
BFS 的时候如果没法连到汇点了，就返回。
时间复杂度是 \(O(V^2E)\) 的（只需要记结论就好了，证明试试看能否看懂。加了以下几个优化之后，是依旧很松的上界，一般可以跑 \(10000 \sim 100000\) 的数据）
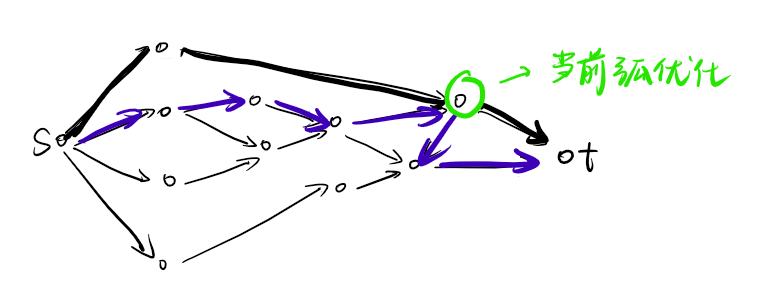
当前弧优化：我们走到一个点的时候，正常是按照邻接表的顺序遍历一遍它的邻边。假设我们在一条残量网络中从 \(s\) 沿一条路径走到节点 \(v\)，这条路的最大流量是 \(limit\)。走过了 \(v\) 的第 \(1\) 条边之后又走到了第 \(2\) 条边，那么第 \(1\) 条边的容量一定小于 \(limit\)，那么在加上这一次增广路之后的残量网络中第 \(1\) 条边一定不会被增广，下一次可以直接从第 \(2\) 条边搜索。（需要注意的是虽然第 \(2\) 条边被搜索过，但是这一条边不一定流满了，下次还需要搜）。因此我们记录当前弧 \(x_i\) 表示在第 \(i\) 个点时需要从什么位置开始搜索，我们搜到第几条边就把 \(x_i\) 更新为几。
注意当前弧在每次 BFS 时重置，否则退流没法处理。作用如下图，当蓝色的边经过绿点的时候直接跳过了已经走的黑色边。（假设已经流满了这条边，也就是说已经走到了下一条边。）
删点优化：DFS的时候我们的入口是 \(dfs(i,limit)\)，返回的是从 \(i\) 到 \(t\)，之前最大流量为 \(limit\)。如果返回的是 \(0\)，那么从这个点到汇点没有路径了，这时候直接将其删除避免重复搜索。怎么删除？把层数设为 \(-1\) 即可。
满流剪枝：当流量已经 \(==limit\) 的时候就不需要继续搜索了。
这个算法一定要把板子记下来，很重要！一般都用这个板子。并且三个优化的细节都要记一下。
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int n, m, s, t; int cnt = 0;
int head[100010], nxt[2000010], to[2000010], c[2000010];
int d[100010]; int cur[100010]; //当前弧优化
void add(int u, int v, int w) {
nxt[cnt] = head[u], to[cnt] = v, c[cnt] = w; head[u] = cnt++;
nxt[cnt] = head[v], to[cnt] = u, c[cnt] = 0; head[v] = cnt++;
}
bool bfs() {
queue<int> q; memset(d, -1, sizeof d); d[s] = 0; q.push(s); cur[s] = head[s]; //当前弧初始值为head
while(!q.empty()) {
int u = q.front(); q.pop();
if(u == t) return 1;
for(int i = head[u]; ~i; i = nxt[i]) {
int v = to[i];
if(d[v] >= 0 || !c[i]) continue;
d[v] = d[u] + 1; cur[u] = head[u];
q.push(v);
}
}
return 0;
}
int find(int u, int limit) {
if(u == t) return limit;
int flow = 0;
for(int i = cur[u]; ~i && flow < limit/*满流剪枝*/; i = nxt[i]) {
cur[u] = i;
int v = to[i];
if(d[v] == d[u] + 1 && c[i]) {
int f = find(v, min(c[i], limit - flow));
if(!f) d[v] = -1;//删点优化
c[i] -= f; c[i^1] += f; flow += f;
}
}
return flow;
}
int dinic() {
int maxflow = 0, flow;
while(bfs()) while(flow = find(s, inf)) maxflow += flow;
return maxflow;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//think twice,code once.
//think once,debug forever.
cin >> n >> m >> s >> t; memset(head, -1, sizeof head);
f(i, 1, m) {int u, v, w; cin >> u >> v >> w; add(u,v,w);}
cout << dinic() << endl;
return 0;
}
1.6 最大流建模
可以用最大流建模的问题一般是找一个集合的最值，我们需要保证：
- 建图之后的每一个可行流和原问题每一个可行解是一一对应的。
那么，图的最大流就是原问题的最优可行解。
（和动态规划很像，都要靠直觉）
举个例子：二分图最大匹配问题。
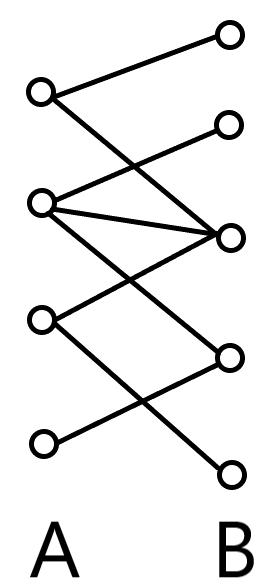
最大流模型中我们建立一个源点和汇点，并把源点向每一个 \(A\) 集合的点连一条容量为 \(1\) 的边；把每一个 \(B\) 集合的点向汇点连一条容量为 \(1\) 的边；\(A\) 集合和 \(B\) 集合之间的每一条边（原图上的边）容量都为 \(1\)。如下图：
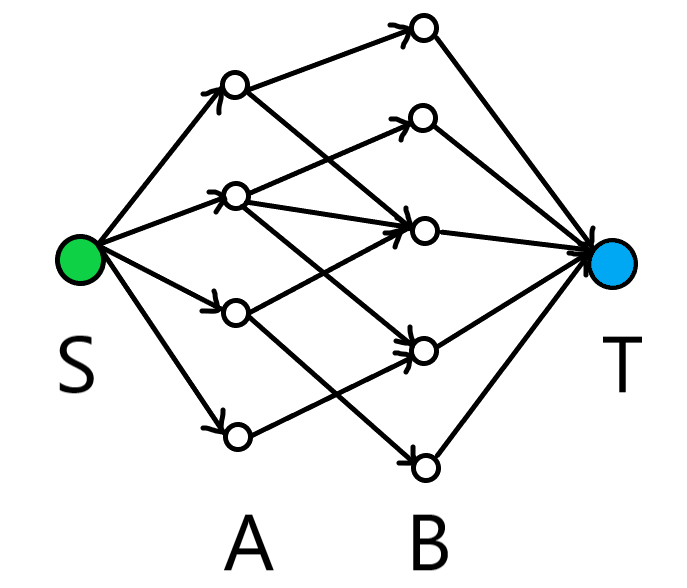
考虑原图上的一个可行解 \(s\) 一定对应到网络中一个可行流 \(f\)：（考虑流量守恒和容量限制是否满足）
当原图上两个点 \(u,v\) 通过边 \(e\) 匹配时，网络上存在边：\(s \rightarrow u,u \rightarrow v,v \rightarrow t\)。这时流量为 \(1\)，等于原问题匹配个数。
考虑网络上一个可行流 \(f\) 一定对应到网络中一个可行解 \(s\)：
对于网络上的容量限制，我们发现一个点只能被选中一次，只能连原图上的一条边。这也就是可行解的要求。注意该网络的流量可以有实数，所以我们需要加上一个限定：网络上整数值可行流的集合为原图上可行解的集合。由于我们的 Dinic 算法计算的时候一直使用整型变量，所以满足找到的都是整数值可行流。此时找到的就是整数值最大流等于原问题最优解，因此可以这样建模。
Dinic 更优秀地解决二分图最大匹配问题。
二分图最大匹配一般使用匈牙利算法，时间复杂度 \(O(VE)\)，但是使用 Dinic 算法可以做到 \(O(E\sqrt V)\)。怎么理解呢？匈牙利算法相当于每次找一条增广路，相当于 FF 算法或 EK 算法，Dinic 比它快就很容易理解了。
如果要输出方案，由于最后剩下的是最大流的残量网络，所以可以考虑在残量网络上遍历原图上的每一条正向边（要搞清楚编号范围是什么），如果容量为 \(0\)，那么代表这条边的流量为 \(1\)，输出这两个点即可。
结论：dinic 算法在执行 \(k\) 轮之后增广路的长度都至少是 \(k\)。
1.7 多源汇和关键边
多源汇：有若干个 \(S\) 和若干个 \(T\)，求最大流。
分析：直接建超源超汇即可。注意到最短路模型也可以这么做，并且不会退化时间复杂度，BFS 会变成 01BFS。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
#define cerr if(false)cerr
#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍！
int S,T,s[10010],t[10010],cnt=-1;int n,m,sc,tc;
int head[10010],to[300010],nxt[300010],cur[10010],cap[300010],dep[10010];
void add(int u,int v,int w){
nxt[++cnt]=head[u];to[cnt]=v;cap[cnt]=w;head[u]=cnt;
nxt[++cnt]=head[v];to[cnt]=u;cap[cnt]=0;head[v]=cnt;
}
bool bfs(){
memset(dep,-1,sizeof(dep));queue<int>q; q.push(S);cur[S]=head[S];dep[S]=0;
while(!q.empty()){
int now=q.front();q.pop();
for(int i=head[now];~i;i=nxt[i]){
if(cap[i]>0&&dep[to[i]]==-1){dep[to[i]]=dep[now]+1;q.push(to[i]);cur[to[i]]=head[to[i]];}
if(to[i]==T)return 1;
}
}
return 0;
}
int find(int now,int limit){
cerr<<now<<" "<<dep[now]<<" "<<limit<<endl;
if(now==T)return limit;
int flow=0;
for(int i=cur[now];~i&&flow<limit;i=nxt[i]){
cur[now]=i; if(dep[to[i]]!=dep[now]+1||cap[i]==0)continue;
int tmp=find(to[i], min(cap[i],limit-flow));
if(tmp==0)dep[to[i]]=-1;
flow+=tmp;cap[i]-=tmp;cap[i^1]+=tmp;
}
return flow;
}
int dinic(){
int flow=0,maxflow=0;
while(bfs()) {f(i, 0, n + 1){cerr<<dep[i]<<" ";}cerr<<endl;flow = find(S,inf); cerr<<flow<<endl; maxflow+=flow;}
return maxflow;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin>>n>>m>>sc>>tc; memset(head,-1,sizeof(head));
f(i,1,sc)cin>>s[i]; f(i,1,tc)cin>>t[i];
S=0,T=n+1; f(i,1,sc)add(S,s[i],inf); f(i,1,tc)add(t[i],T,inf);
f(i,1,m){int u,v,w;cin>>u>>v>>w;add(u,v,w);}
cout<<dinic()<<endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
关键边：求有哪些边使得其增加容量可以导致最大流变大。
分析：考虑 \(s\) 到 \(u\) 有一条增广路径，\(v\) 到 \(t\) 有一条增广路径，并且 \(u\) 到 \(v\) 满流的话，\(u\) 到 \(v\) 是一条关键边。（注意求的是原图里的关键边，而不是残量网络里）
直接从 \(s\) 和 \(t\) 开始分别跑正向和反向 DFS 即可。
（可以记为\(s \rightsquigarrow u \rightarrow v \rightsquigarrow t\)）
证明：首先如果并不满流，显然不行。其次满流的话是充要条件：若有这两条路径，这条边增加容量可以让其联通；否则增加这条边之后不论水想往哪里流出去一定会被堵住。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
#define cerr if(false)cerr
#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍！
int cnt=-1;int n,m,S,T;
int head[550],from[12010],to[12010],nxt[12010],cap[12010],cur[550],dep[550];
void add(int u,int v,int w){
nxt[++cnt]=head[u];from[cnt]=u;to[cnt]=v;cap[cnt]=w;head[u]=cnt;
nxt[++cnt]=head[v];from[cnt]=v;to[cnt]=u;cap[cnt]=0;head[v]=cnt;
}
bool bfs(){
memset(dep,-1,sizeof(dep));queue<int>q;q.push(S);cur[S]=head[S];dep[S]=0;
while(!q.empty()){
int now=q.front();q.pop();
for(int i=head[now];~i;i=nxt[i]){
if(cap[i]>0&&dep[to[i]]==-1){
dep[to[i]]=dep[now]+1;q.push(to[i]);cur[to[i]]=head[to[i]];if(to[i]==T)return 1;
}
}
}
return 0;
}
int find(int now,int limit){
cerr<<now<<" "<<limit<<endl;
if(now==T)return limit;
int flow=0;
for(int i=cur[now];~i&&flow<limit;i=nxt[i]){
cur[now]=i;if(cap[i]==0||dep[to[i]]!=dep[now]+1)continue;
int tmp=find(to[i],min(cap[i],limit-flow));
cerr<<tmp<<endl;
if(tmp==0)dep[to[i]]=-1;
flow+=tmp;cap[i]-=tmp;cap[i^1]+=tmp;
}
return flow;
}
int dinic(){
int maxflow=0;
while(bfs()){cerr<<"success\n";maxflow+=find(S,inf);cerr<<maxflow<<endl;}
return maxflow;
}
bool rs[510],rt[510];
void dfs(int now,bool* r,int k){
r[now]=1;
for(int i = head[now]; ~i; i=nxt[i]){
if(cap[i^k]>0&&!r[to[i]]){
r[to[i]]=1;
dfs(to[i],r,k);
}
}
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin>>n>>m; S=0;T=n-1;memset(head,-1,sizeof(head));
f(i,1,m){int u,v,w;cin>>u>>v>>w;add(u,v,w);}
//cout<<
dinic();//<<endl;
dfs(S,rs,0);dfs(T,rt,1); int ans=0;
f(i,0,n-1)cerr<<rs[i]<<" "<<rt[i]<<endl;
for(int i = 0; i <= cnt; i += 2) {
if(cap[i]==0&&rs[from[i]]&&rt[to[i]])ans++;
}
cout<<ans<<endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
1.8 拆点
网络流的两个限制：容量限制和流量守恒，前一个是针对边的，可以很灵活地变化；而后一个是针对点的，但变化不灵活。我们如果想要针对点做限制（譬如，经过某个点的流量有限制）该怎么办呢？
这就引出了拆点。考虑对点 \(i\) 分成入点和出点，其他点连入 \(i\) 的点都连向 \(i_入\)；\(i\) 连出的点都连向 \(i_出\)。从 \(i_入\) 连向 \(i_出\) 一条边，就可以实现对点做限制。
1.9 三分图最大匹配问题
农场里 \(n\) 种食物，\(m\) 种饮品，\(k\) 头奶牛，每头奶牛有爱吃的食物和爱喝的饮料，分别只有一种。每种食物和饮品只有一份。每头奶牛吃一份食物。求分配方式，使得有吃有喝的奶牛最多。
可以直接对中间的节点拆点，使得其包含点的限制。
2 最小割模型
重复一下定义：
割：将图分成 \(A, B\) 两个点集，保证 \(S \in A, T \in B\)。
割容量：\(\sum \limits_{i \in A, j \in B} c_{i \rightarrow j}\)。（注意没有第二项）
考虑怎么求最小割的边集（形象理解最小割）。对于跑完最大流的原图，有一些关键边，其中的一些会作为最小割的边集。我们从 \(S\) 出发，经过原图上的剩余容量不为 \(0\) 的边，可以到达的点集作为集合 \(A\)，其他点作为集合 \(B\)。
另外，对于任意一组流，其不一定满流，所以生成的割并不一定等于流量。
网络战争
【题意】
给定一个无向图 \((V, E)\)，给定两个点 \(S, T\)，边有边权，求一个边集 \(e \in E\)，使得 \(\cfrac{\sum w}{|e|}\) 最小，并且断开这些边能够使得 \(S, T\) 不连通。
【分析】
看到这个平均数式子，用 01 分数规划的固定套路是二分答案 \(mid\)，然后转化为 \(\sum w - mid \ge 0\)。于是我们考虑将所有边权减去 \(mid\)。
然后注意一下这个割集怎么求。
首先，最小割并不等于题目所求的最小的割集，因为可能存在边权为负数的 \(A, B\) 内部边，选上比不选好，所以最小割的集合不一定包含题目的最小割集。
自然地想到边权是负数的边一定要选，把它们删掉即可。考虑正数的边，那么这时候最小割就等于最小割集了。
还有一个问题：无向图，怎么办。其实这也是一个套路，对于每条边，建立两条反向的有向边，考虑这个的正确性：由于最大流最小割定理，我们希望求出的是原图的最小割（无向图意义下），也就是有一些边作为关键边。考虑某一条割边，肯定按照两端分别属于哪个集合给它定一个方向。其他边任意定向。考虑这时候图变成有向图。我们需要把这个有向图能够求出来。也就是，对于某个流 \(f\)，某条边只有一个流向，并且这个流向和选择的有向图方向一致。
也即考虑是否能够办到：
- 对于原问题的每一个解，存在一个流，使得每条边只有一个流向，而且与解的流向对应。
- 对于每一个流，其得到的流量不会超过所有原解集的流量。
第一个显然可以办到，我们考虑第二个：如果两条边都有流量，我们可以对两条边的流量进行相互抵消，使得其流量不变，并且可以对应到第一种情况。
于是我们对每条边建两个方向的边，容量都是 \(c\)，是对的。
2.1 集合划分模型
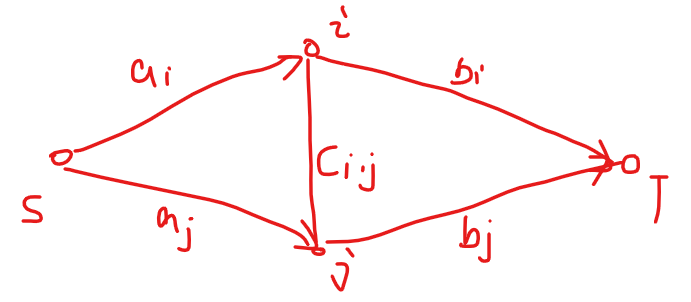
一堆元素，第 \(i\) 个划分到 A 组会有 \(a_i\) 的贡献，划分到 B 组会有 \(b_i\) 的贡献；\(i, j\) 之间有一些有限制：如果分到不同组会有 \(c_{i,j}\) 的贡献，求最小贡献。
这是最小割最重要的一个模型，一些常见的模型都是由此推得。
建图方式：建立 S, T，从 \(i\) 向 S 连一个 \(a_i\) 边，向 T 连一个 \(b_i\) 边，\(i, j\) 连一个双向的 \(c_{i,j}\) 边，求它的最小割即可。注意最大流生成的最小割一条路径有且只会有一条边被割，如果割 \(i\) S 边那么说明 \(i\) 分到 A 组；否则分到 B 组。考虑两种情况：
- 两个都割了同一条边，那么中间不需要割；
- 否则需要割，算上 \(c_{i,j}\) 贡献。
3 关于二分图的一些性质
最大流等于最小割，最小点割集等于最小边割集。
第一个推论就是 hall 定理。
hall 定理：对于一个二分图，存在一个匹配使得其左部点每个点都能匹配到某个点，当且仅当对于任意左部点集合，其邻域的大小 \(\ge\) 其集合大小。原因是，对于任意一个集合，其连通度为集合大小，所以最大流等于左部点个数。
其直接推论：每一个点度数都一样（左右点一起算）的二分图，一定存在完美匹配（最大匹配是 \(\min(l, r)\)）。
然后最小边割集等于最大流（最大匹配），最小点割集也等于最大流，于是最小点覆盖（选一些点，使得每一条边至少一个端点在选的点上）等于最大流（删掉这些点，没有边能够到达）；最大独立集是最小点覆盖的对偶问题，它等于点数减去最小点覆盖。
考虑 dag 的最小路径覆盖（使用最少的路径，覆盖每个点至少一次）：建立一个新图，每个点拆成出入点，按照原图连边，在路径上，前连到后。没得连的，就是路径尾部，于是算出了路径条数=点数-新图最大匹配。
链，指一个点径 \(v_1, ..., v_k\)，使得 \(\forall i, \exist v_i \rightsquigarrow v_{i+1}\)。
对于一个偏序，链等于路径，所以最小链覆盖等于最小路径覆盖。最长反链指的是 \(v_1, ..., v_k\)，使得 \(\forall i, j, \not \exist v_i \rightsquigarrow v_j\)（两两没有边），其等于最小链覆盖（Dilworth 定理）。
这个性质有什么作用呢？比如我们有一个 DAG，定义一个偏序关系为 \(x \preceq y\)，表示 \(x\) 能到达 \(y\)。那么如果需要求一组最大的点集使得它们互相都不能到达，那么这就是一条最长反链，等于最小链覆盖。
3.1反悔贪心
遇到一个问题：有 \(n\) 个位置，一个位置上可能有 \((, )\) 或者两者可以选一个的 \(?\)。求最大括号匹配。
这个问题可以反悔贪心，维护两个集合，分别维护可以匹配的左端点，以及目前做了 \()\) 的通配符，对于一个 \((\)，直接加入第一个集合；对于一个 \()\)，考虑第一个集合是否非空，如果是就匹配，否则考虑第二个集合是否有元素，如果有，令其成为 \((\)，并且当前这个括号和原来这个通配符所匹配的元素匹配。对于一个 \(?\)，首先判断是否可以成为 \()\)，如果可以的话要注意加入第二个集合；否则加入第一个集合。
这个反悔贪心为什么正确？有没有等价的贪法？有没有对应到网络流的做法？
