组合游戏
update:2022.8.2,完善了内容。
IOI2009集训队论文:贾志豪《组合游戏略述——浅谈SG游戏的若干拓展及变形》
从 nim 博弈说起
甲,乙两个人玩 nim 取石子游戏。
nim 游戏的规则是这样的:地上有 \(n\) 堆石子(每堆石子数量小于 \(10^4\)),每人每次可从任意一堆石子里取出任意多枚石子扔掉,可以取完,不能不取。每次只能从一堆里取。最后没石子可取的人就输了。假如甲是先手,且告诉你这 \(n\) 堆石子的数量,他想知道是否存在先手必胜的策略。
分析:
- 如果只有一堆石子,第一个人拿走所有石子,一定会赢。
- 如果有两堆相同的石子,第一个人拿多少石子,第二个人就在另一堆拿一样个数的石子,最后第一个人一定会输。
- 考虑将石子数表示为状态 \((a_1,a_2,a_3,...)\)。考虑如果知道 \(s=(a_1,a_2,...,a_m)\) 和 \(t=(b_1,b_2,...,b_n)\) 的胜负性(先手是不是必胜),那么可以叠加地求出 \(s+t=(a_1,a_2,...,a_m,b_1,b_2,...,b_m)\) 的胜负性。
如果 \(s\) 和 \(t\) 都为负,那么先拿的人拿走一堆中的某些石子之后,后拿的人可以按照必胜策略拿同一堆石子。如果这一整堆石子拿完了,那么另外一堆也一样。如果先拿的这个人率先取了另一堆的石子,后拿的人也可以按照相应必胜策略应对。总之,最后是先拿的人输,即 \(s+t\) 负。
如果 \(s\) 和 \(t\) 有一个为胜一个为负,那么先拿的人在胜的那一堆里按照必胜策略拿取一些石子,局面变为负+负,此时一开始后拿的人拿了,必负。故先拿的人赢,即 \(s+t\) 胜。
如果 \(s\) 和 \(t\) 都为胜,那么不确定。 - \((x_1,x_1,x_2,...)\) 的胜负性等于 \((x_2,...)\) 的胜负性,因为相当于拆成 \((x_1,x_1)\) 负和 \((x_2,...)\),这个东西的正负性由 \(3\) 知道就是 \((x_2,...)\) 的正负性。
这样的好处是,我们可以将一个状态变成里面的元素都不一样的。 - 考虑 \(\#s\) 为 \(s\) 状态中所有数的异或和。那么我们有如下状态合并法则:
- \(a==b\),那么 \(\#s=0\)。
- \(a==(k),b==0\),那么 \(\#s=k\)。
- \(a==0,b==(k)\),那么 \(\#s=k\)。
- \(a==0,b==0\),那么 \(\#s=0\)。
发现这个东西非常像刚刚的状态胜负性合并法则。具体地说,如果 \(a\) 和 \(b\) 满足如上条件,那么 \(\#s\) 为 \(0\) 的话胜负性为负,否则为正。
- 证明这个东西,即 \(\#s\) 等于正负性。
如果 \(\#s \ge 0\),假设其最高位为 \(i\),取 \(s\) 中一个第 \(i\) 位是 \(1\) 的数,将其记为 \(a\),其他数记为 \(t\)。那么 \(\#s=\#a ⊕ \#t\)。让第一个人取 \(s\) 这一堆里面的石子,使剩下的个数为 \(\#a ⊕ \#s < \#s\),那么剩下的东西的 \(\#\) 是 \(\#a ⊕ \#s ⊕ \#t = 0\)。那么如果有 \(\#s>0\),那么一定有一种取法 \(s->t\) 使得 \(\#t==0\)。
易证,如果有 \(\#s=0\),那么无论哪一种取法 \(s->t\) 都使得 \(\#t>0\)。
因为个数一直减小,所以最后得到一堆 \(\#k=0\) 时,先手胜。
综上所述,\(\#s>0\) 的时候,先手必胜。\(\#s==0\) 的时候,后手必胜。
结论:
如果这些石子的数量异或和为 \(0\),后手必胜;否则先手必胜。
推广:
- 如果每次只能取不超过 \(m\) 个:
若所有石子模 \(m\) 的异或和不为 \(0\),则先手胜,反之则后手胜。 - 通法:\(SG\) 函数
我们用一个 \(n\) 元组 \((a_1,a_2,...,a_n)\) 描述过程中的一个场面。
用 \(\#s\),表示局面 \(s\) 对应的二进制数。
如果局面 \(s\) 只有一堆石子,那么用这一堆石子数目所对应的二进制数来表示 \(\#S\)。
设局面 \(S=(a_1, a_2, …, a_n)\),\(\#S=\#a_1+\#a_2+…+\#a_n\),采用异或操作。
但是这里的 \(\#a_i\) 并不是一直都等于本身的二进制数的,而是应该换作一个函数,这个函数,根据题目的不同而有所不同。
这,就是 \(SG\) 函数
通常解法: 首先,把原局面分解成多个独立的子局面,则原游戏的 \(SG\) 函数值是它的所有子局面的 \(SG\) 函数值的异或和。
即 \(SG(S)=SG(s_1) ⊕ SG(s_2) ⊕ ... ⊕ SG(s_n)\)。
然后,分别考虑每一个子局面,计算其 \(SG\) 值。
后手必胜当且仅当 \(SG\) 的异或和为 \(0\)。
SG 函数
那么我们来系统地介绍一下什么叫 SG 函数。
像这样,满足以下条件的游戏为公平组合游戏:
- 一个局面所能转移到的局面只由局面本身决定,不由游戏者身份决定。(围棋,象棋等就不是,因为不可以操作对方的棋子)
- 首先不能操作的人失败。
如果对每一个局面建点,一个局面可以到达另一个局面的话建一个有向边如下:
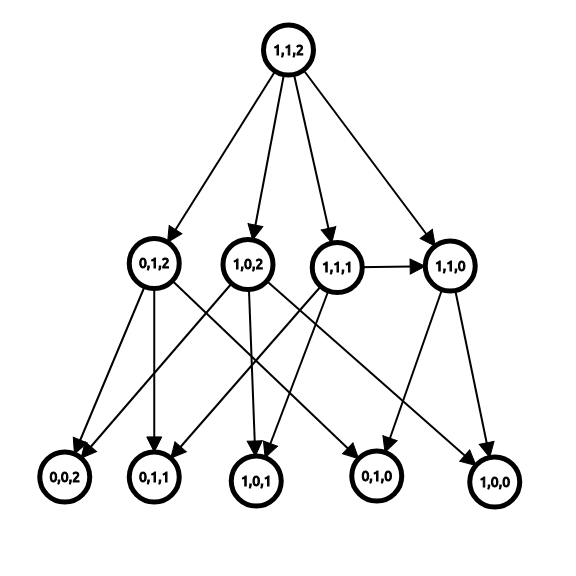
定义必胜状态为先手必胜的状态,必败状态为先手必败的状态,那么有以下三条定律:
- 如果一个点没有后继状态,那么它是必败状态。
- 如果一个点的后继状态中有必败状态,那么它是必胜状态。
- 如果一个点的后继状态都是必胜状态,那么它是必败状态。
如果博弈图是一个有向无环图,那么这个游戏叫做有向图游戏,那么通过这三个定理我们可以在绘出该图的情况下 \(O(N+M)\),其中 \(N\) 为状态数,\(M\) 为边数,得到每个状态是必胜还是必败状态。
但建边的复杂度可能要达到 \(O(N^2)\),常常是难以接受的。有没有更好一些的方法呢?SG 函数就是简化了这一过程的方法。
定义 \(\operatorname{mex}\) 函数值为不属于集合 \(S\) 中的最小自然数。例如 \(\operatorname{mex}\{0,2,4\}=1,\operatorname{mex}\{1,2\}=0\)。
对于有后继节点 \(y_1,y_2,...,y_k\) 的节点 \(x\),定义其 \(SG\) 函数为:
对于起点为 \(s\) 的有向图游戏,如果 \(SG(s)=0\),那么该游戏先手必败,否则先手必胜。原因:
- 如果一个节点没有后继节点,那么其 SG 函数一定为 \(0\)。
- 如果当前走到 SG 函数不为 \(0\) 的节点,那么下一步一定可以走到 SG 函数为 \(0\) 的节点。
- 如果当前走到 SG 函数为 \(0\) 的节点,那么下一步只能走到 SG 函数不为 \(0\) 的节点。当这个节点不存在时就输了,这点和二分图博弈有相似之处。
对于由 \(n\) 个有向图游戏组成的组合游戏,起点分别为 \(s_1,s_2,...,s_n\),失败条件为这 \(n\) 个有向图游戏均无路可走。那么当 \(SG(s_1) \oplus SG(s_2) \oplus ... \oplus SG(s_n) \neq 0\) 时先手必胜,否则先手必败。这就是 SG 定理。
证明:(和上面大同小异)
- 如果所有 SG 函数值都为 \(0\),必败。
- 把所有 SG 函数值组成的状态建成一个新的有向图,在这个有向图上面进行有向图游戏。
- 一个节点不可能走到和其异或和一样的节点,因为如果要这么走,必须从一个 SG 为 \(k\) 的节点走向另一个 SG 为 \(k\) 的节点,那么前面一个节点的 SG 值一定不是 \(k\)。
- 如果要将一个异或和为 \(k\) 的节点改成异或和为 \(0\) 的节点,做如下操作:对于 \(k\) 的最高位,是 \(1\),找到 SG 值这一位为 \(1\) 的元素,记为 \(a\)。那么需要将 \(a\) 改成所有 SG 值中除了 \(a\) 其他所有 SG 值的异或和。因为这个异或和必定为 \(0\),所以这个异或和小于 \(a\)。那么一定合法。
- 所以不论从哪一个节点走都可以立刻走到异或和为 \(0\) 的节点。
- 异或和为 \(0\) 的节点只能走到异或和不为 \(0\) 的节点。
回顾 nim 游戏,发现可以用这个角度证明结论:对于单个场面,由于每一个节点都能到达比它小的任意节点,所以 \(SG(x)=x\)。再根据 SG 定理,就可以得出 Nim 和的结论了。
https://ac.nowcoder.com/acm/contest/34655
C
题意:有若干堆石子,每堆石子初始有 \(c_i\) 个,最多放 \(s_i\) 个。每次可以往任意一堆里加石子,如果原来有 \(k_i\) 个石子,那么加的数量范围为 \(1 \sim k_i^2\)。
分析:SG 函数找性质非常重要。对于本题的 SG 函数(考虑一堆),容易发现当 \(k + k^2 \ge s\) 的时候 \(SG(k)=s-k\)。
当 \(k + k^2 < s\) 但 \((k+1)+(k+1)^2 \ge s\) 的时候是临界点,有 \(SG(k)=0\)。
这时候我们找到必败点,可以递归问题,\(SG(k,s)=SG(k,m)\),其中 \(m\) 为刚刚的必败点。
可以预处理出这个分界点。但这里写法是从 \(\sqrt s\) 开始找,也是可以的。
时间复杂度,每次跳到 \(\sqrt s\),应该是 \(O(n \log k)\) 的。
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int lst[1000010];
int calc(int s, int c) {
int mx = sqrt(s);
while(mx + mx *mx >= s) mx--;
if(c > mx) return s - c;
else if(c == mx) return 0;
else return calc(mx, c);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//think twice,code once.
//think once,debug forever.
int n; cin >> n; int ans = 0;
f(i,1,n){
int s, c;
cin >> s >> c;
ans ^= calc(s, c);
}
cout<<(ans==0?"No\n":"Yes\n");
return 0;
}
F
反 nim 博弈变种。
先来介绍普通的反 nim 博弈:和 nim 博弈一样,有 \(n\) 堆石子,每次可以取其中一堆的任意个,最后一个取的人失败。
同样从异或和入手。\(\operatorname{mex}\) 的异或和的性质主要是:
- 异或和为 \(0\) 的只能跳到不为 \(0\) 的。
- 异或和不为 \(0\) 的一定可以跳到异或和为 \(0\) 的。
- 公平组合游戏下,异或和为 \(0\) 的里面有一些必败策略。
考虑反常游戏下前两条依然适用。
把异或和为 \(0\) 的状态叫做 \(A\),异或和和不为 \(0\) 的状态叫做 \(B\)。考虑不只有一个石子的堆(简称充裕堆)的个数:没有的状态叫做 \(0\),有一个叫做 \(1\),有不止一个叫做 \(2\)。
那么我们有五种状态:\(A0,A2,B0,B1,B2\)。考虑这几种情况的结果:
- \(A0\) 显然必胜,\(B0\) 显然必败。
- 对于 \(B1\),先手转化为 \(B0\) 即可。必胜。
- \(A2\) 只可以转化为 \(B1,B2\)。
- 若 \(A2\) 转化为 \(B1\),那么会输。若 \(A2\) 转化为 \(B2\),那么 \(B2\) 直接转回 \(A2\)(这里有一个特例要判掉:选择 \(a\) 的时候,如果除了 \(a\) 其他所有 SG 值的异或和为 \(1\)(也就是需要变成 \(1\)),那么仍然是 \(B2\),因为如果这个 \(1\) 是一个 \(1\) 创造的,那么原情况是 \(A1\)。否则一定是两个以上的充裕堆创造的)即可。
综上所述,\(A0,B1,B2\) 必胜;\(B0,A2\) 必败。
注意到为什么增加了一个 \(0,1,2\) 的状态,因为本题由于特殊的结算规则,之前的已经不够用了。做题的时候甚至可以分得更细,最后合并,殊途同归。
那么本题增加了一个“可以把一堆苹果分成两堆”的规则。如法炮制来探讨一下:
- \(A0,B0,B1\) 的结果没有任何变化。
- \(A2\) 可以变化成 \(A2\) 吗?虽然增加了一种一堆变两堆的方法,但是由于 \(a \oplus b \le a + b\),而变化之后两堆加起来一定不大于 \(x-1\),所以不可能。还是必须变成 \(B1\) 或者 \(B2\)。
- \(B2\) 好好走还是能赢。
因此完全一致。
对于任意 ANTI-SG 游戏,有:对于任意一个 Anti-SG 游戏,如果我们规定当局面中所有的单一游戏的 SG 值为 \(0\) 时,游戏结束,则先手必胜当且仅当:
(1)游戏的 SG 函数不为 0 且游戏中某个单一游戏的 SG 函数大于 1;
(2)游戏的 SG 函数为 0 且游戏中没有单一游戏的 SG 函数大于 1。
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int a[110];
int cnt = 0;
int ans = 0;
int main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//think twice,code once.
//think once,debug forever.
int n; cin >> n;
f(i,1,n)cin>>a[i];
f(i,1,n){
if(a[i]>=2)cnt++;
ans ^= a[i];
}
if((cnt >= 1 && ans > 0) || (cnt == 0 && ans == 0)) cout << "Yes\n";
else cout << "No\n";
return 0;
}
I
删边游戏。
对于一棵树,每次可以删除一个子树,不能操作的失败。
结论:我们递归计算 SG 值。对于叶子节点 SG 值为 \(0\)。对于其他节点,SG 值为(所有子节点的 SG 值 \(+1\)) 的异或和。
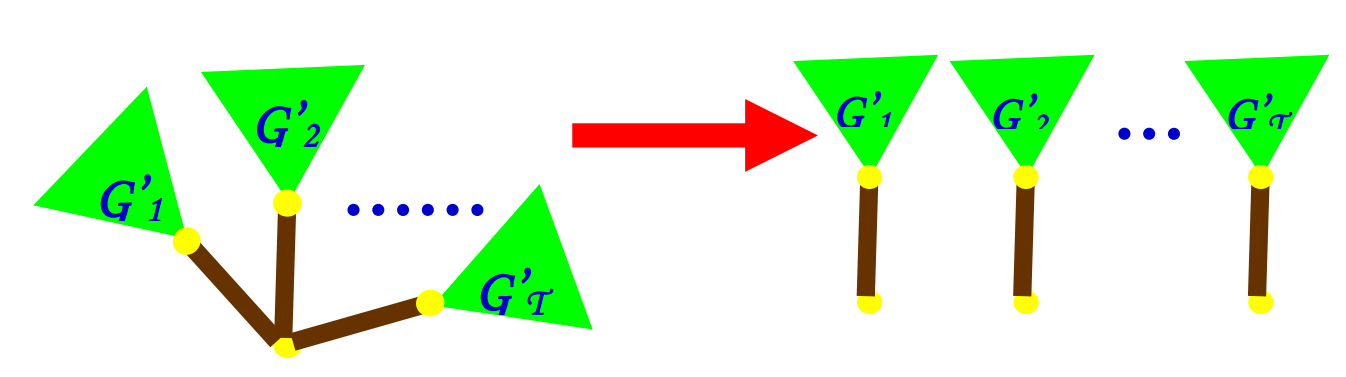
证明:使用数学归纳法证明。在证明之前需要先提到重要突破口:一个根节点有若干个子树组成的游戏,相当于每一个子树带一个根节点组成的多个游戏之和。如下图:
容易发现当 \(k=1\) 或 \(2\) 的时候满足公式。
假设有 \(k\) 个节点时任意情况均满足该 SG 和计算公式。那么以下证明具有 \(k+1\) 个节点的情况仍然成立。
对于根节点有一个子结点的树来说,假设根为 \(A\),其子节点为 \(B\),\(B\) 子树的 SG 值为 \(SG_B\)。那么我们如果删除 \(A-B\) 这条边,就会达成 \(0\) 的 SG 值。如果不删除这条边,删除 \(B\) 字数上的任意一条边,那么 \(B\) 这棵树可以转化成 SG 值为 \(0 \sim SG_B-1\) 的任意一个。由于剩下的点数 \(\le k\),那么满足上述公式,\(A\) 这棵树可以转化为 SG 值为 \(1 \sim SG_B\) 的任意一个。综上所述,进行一次操作之后可以变成 \(0 \sim SG_B\) 中的一个,那么其 SG 值为 \(SG_B+1\)。
对于根节点有多个子结点的树来说,由重要突破口得知 \(SG_A=SG_{G'_1} \oplus SG_{G'_2} \oplus...\oplus SG_{G'_T}\)。
那么原公式成立。
CF1704F
题意:给定一个长度为 \(n\) 的 RB 串,Alice 的操作可以选择两个连续的字符染成 W,要求这两个字符必须有一个是 R。Bob 可以选择两个连续的字符染成 W,要求这两个字符必须有一个是 B。Alice 先行动,无法操作的人输了。问谁能够获胜?
\(n \le 2 \times 10^5\)
分析:这里 R 相当于 Alice 的“筹码”,“筹码”没了肯定会输。那么最优策略就是尽可能少地浪费自己的筹码,如果可以的话拉一个对方的筹码垫背。
那么一定是一开始两个人都删除若干个 RB 或 BR,没有了的话就删除一个(而不是两个)自己的筹码。如果筹码数不相等,少的人就寄了。
如果筹码数相等,那么先无法删除 RB 或 BR 的人输了。每个人都只能取 RB 或 BR,那么变成了公平组合游戏。有若干个 RB 相间的串构成了若干个有向图游戏。计算 \(SG_i\),表示长度为 \(i\) 的串的 SG 值。一个可以分成多个,并且满足 DAG,可以从小到大求。但是这是 \(O(n^2)\) 的。
观察打表发现OEIS,有一个循环节。时间降到 \(O(n)\)。(牛逼!)(这东西叫 Dawson's Chess,见过了以后不能再不知道了。
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
const int m = 500000;
int sg[500010];
bool vis[1010];
char c[500010];
int main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//think twice,code once.
//think once,debug forever.
sg[0] = 0;
f(i, 1, m) {
if(i <= 87) {
memset(vis, 0,sizeof vis);
f(j, 0, i - 2) {
vis[(sg[j]^sg[i-2-j])]=1;
}
f(j, 0, m) if(!vis[j]) {sg[i] = j;break;}
}
else sg[i] = sg[i - 34];
}
int t; cin >> t;
while(t--) {
int n; cin >> n;
int ans = 0; int b = 0, r = 0; int cmp = 0;
f(i,1,n) {
cin>>c[i];
if(c[i] == 'B') b++; if(c[i] == 'R') r++;
if(i != 1 && c[i] != c[i - 1]) cmp++;
else {
ans ^= sg[cmp + 1]; cmp = 0;
}
}
ans ^= sg[cmp + 1]; cmp = 0;
if(b != r) cout<<(b>r?"Bob\n":"Alice\n");
else cout<<(ans?"Alice\n":"Bob\n");
}
return 0;
}
ABC278G
【题意】
桌子上有 \(1 \sim n\) 一共 \(n\) 个数字。先手开始,每次可以拿走桌上的 \(i \in [l, r]\) 个数字。不能拿的人输了。请和交互库玩游戏,可以选择先手或者后手。
\(n \le 2000\)
【分析】
众所周知,atcoder 一秒可以过 \(1e10\)。因此可以:暴力计算 SG,然后对于每个局面,使用 SG 定理的证明,也就是如果 \(a \oplus b = x\),其中 \(a\) 为我们想操作的一个区间。那么我们可以把 \(a\) 拆成两个部分使得它们的异或和为 \(b\)。令 \(a\) 为这些区间里拥有 \(xorsum\) 的最高位的即可,因为 \(b\) 的这一位一定为 \(0\)。
- 用 set 维护区间,时间复杂度 \(O(n^3 \log n)\)。
- 预处理每个决策点的操作,时间复杂度 \(O(n^3)\)。
都能过。
考虑正解,这是一个下模仿棋的思路。考虑第一手把这些数字分成相等的两段,然后下模仿棋即可。唯一不能分成两段的是 \(L = R\) 且 \(n\) 和 \(L\) 模 \(2\) 不同余。注意到这时候可以 \(O(n^2)\) 求 SG。
省选联考 2023 D2T1
【题意】
有一个 \(n\) 行 \(m\) 列的棋盘。我们用 \((i,j)\) 表示第 \(i\) 行第 \(j\) 列的位置。棋盘上有一些 障碍,还有一个黑棋子和两个红棋子。
游戏的规则是这样的: 红方先走,黑方后走,双方轮流走棋。红方每次可以选择一个红棋子,向棋盘的相邻一格走一步。具体而言,假设红方选择的这个棋子位置在 \((i,j)\),那么它可以走到 \((i-1,j),(i+1,j),(i,j-1),(i,j+1)\) 中的一个,只要这个目的地在棋盘内且没有障碍且没有红方的另一个棋子。
黑方每次可以将自己的棋子向三个方向之一移动一格。具体地,假设这个黑棋子位置在 \((i,j)\),那么它可以走到 \((i-1,j),(i,j-1),(i,j+1)\) 这三个格子中的一个,只要这个目的地在棋盘内且没有障碍。
在一方行动之前,如果发生以下情况之一,则立即结束游戏,按照如下的规则判断胜负(列在前面的优先):
-
黑棋子位于第一行。此时黑方胜。
-
黑棋子和其中一个红棋子在同一个位置上。此时进行上一步移动的玩家胜。
-
当前玩家不能进行任何合法操作。此时对方胜。
现在假设双方采用最优策略,不会进行不利于自己的移动。也就是说:
- 若存在必胜策略,则会选择所有必胜策略中,不论对方如何操作,本方后续获胜所需步数最大值最少的操作。
- 若不存在必胜策略,但存在不论对方如何行动,自己都不会落败的策略,则会选择任意一种不败策略。
- 若不存在不败策略,则会选择在所有策略中,不论对方如何操作,对方后续获胜所需步数最小值最大的操作。
如果在 \(100^{100^{100}}\) 个回合之后仍不能分出胜负,则认为游戏平局。请求出游戏结束时双方一共移动了多少步,或者判断游戏平局。
【分析】
这题你一看怎么可能是牛逼贪心?这是非公平组合游戏,只能是有向图博弈。这点赛时思考就出问题了。
然后你考虑某一张可能有环的有向图,每个人希望的都是赢/平(无限进行下去)/输往下递推。考虑应当怎么求每一个状态的输赢。
初始一些状态是输的。如果某个状态连到输节点,那么是赢;如果连的有平有赢,那么是平;否则是输。
考虑先把能确定胜负(连向输点/所有连向点均已经确定)这两种的确定了,不难发现这是一个类似拓扑序的过程:对于某个点考虑其 deg = 0 的时候入队;确定赢的时候入队,删掉其所有入边。然后最后剩下的点考虑是什么情况:不会连到输边,但是可能连到平边。于是这些点都是平。(对于任何一个点,都不会主动去选择输掉,于是一直在环上转悠,这是个好的理解方式)
这种有环有向图博弈,你多讨论一些东西就可以了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号