CM-01~03 证明题与思考题 解题报告

七*．本题是一道 noi+/ctsc-级别的思维题。
有三个变量。一开始它们分别存储了正整数 a,b,c（a,b,c 是输入)。比如(4,6,11)。变量可
存储很大的数值。每一步你可以将两个变量相加，相加的结果存入第三个变量。比如(4,6,11)
可以变为 (4,6,10),(4,15,11),(17,6,11)。请问，是否存在一种操作方案，使得三个变量中至少
一个的值变为 N。你只需要输出“Yes”/“No”。数据范围：1≤a,b,c≤30000。1≤N≤1e100。

解：
结论：若能够从 \((a,b,c)\) 中找出两个数 \(m,n\)，使 \(mx+ny=N,x \ge 0,y \ge 0,\gcd(x,y)=1\)，则可以。否则不行。

如果 \(a,b,c\) 其中一个为 \(N\)，一定可以。若不能，我们选定两个数并相加，将加和赋值给另一个数，不妨设这两个数为 \(a\) 和 \(b\)，则三个变量变为 \((b,a+b,a)\)。

之后，我们会不断执行“将两个变量相加，相加的结果存入第三个变量”的过程，直到其中一个值为 \(N\)。

任何一次相加，都得到了 \((x_1a+y_1b,(x_1+x_2)a+(y_1+y_2)b,x_2a+y_2b)\) 的形式，我们将其记为 \((\frac{x_1}{y_1},\frac{x_1+x_2}{y_1+y_2},\frac{x_2}{y_2})\)。

回顾刚刚得到的结果，\((b,a+b,a)=(\frac{0}{1},\frac{1}{1},\frac{1}{0})\)。取其中任意两个值，并将其分子分母分别相加，得到一个新的值，这就是 Stern-Brocot 树由其中一层向下一层递归的过程，得到的三个数就是下图中的一个 V 字形状的三个值。

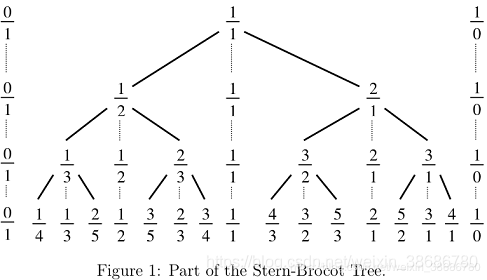
根据 Stern-Brocot 树的相关结论，树上包含所有的既约真分数，不会出现非既约真分数。故若 \(N=ax+by,a \ge 0,b \ge 0,\gcd(a,b)=1\) 则可以根据下面的程序最终得到 \(N\)：

• 找到 \(\frac{x}{y}\) 的位置。
• 若 \(x=0\) 或 \(y=0\)，则另一个数为 \(1\)，显然可以。
• 从Stern-Brocot 树的 \(\frac{1}{1}\) 处出发。若 \(\frac{x}{y}\) 在其左子树下，那么将当前节点和其位于左上方且离它最近的祖先（\(\frac{1}{1}\) 的左右祖先是 \(\frac{0}{1}\) 和 \(\frac{1}{0}\)）加起来得到当前节点的左子节点，并跳向它。若位于右子树下同理。
• 最终会递归到该位置。

若不存在这样的 \(x,y\)，则无法通过第一轮选择 \(a,b\) 相加的方式得到答案。

选择 \(a,c\) 和 \(b,c\) 同理，只要有一个可以成功即可。

六、请手算 n（1 ≤ n ≤ 1e10），使得 n / φ(n) 最大。

解：原式 \(=1/[(1-\cfrac{1}{p_1})(1-\cfrac{1}{p_2})(1-\cfrac{1}{p_3})...(1-\cfrac{1}{p_m})],n=p_1^{a_1}p_2^{a_2}p_3^{a_3}...p_m^{a_m}\)
该式取 \(\max\) 相当于 \((1-\cfrac{1}{p_1})(1-\cfrac{1}{p_2})(1-\cfrac{1}{p_3})...(1-\cfrac{1}{p_m})\) 取 \(\min\)。
由于 \(p_1,p_2,...,p_m\) 各不相等，且越小的素数对原式取 \(\min\) 的贡献越大，故使原式最大的 \(n=2 \times 3 \times ... \times 29=6469693230.\)

四、请手算 1000! mod 1e250。

解：注意到 \(1000! = 10^{249} \times 2^{745} \times \prod p_i^{a_i}\)，其中 \((p_i,1000)=1\)。因此只需要计算 \(2^{745} \times \prod p_i^{a_i}\) 的最后一位即可。
\(2^{745} =2^{512} \times 2^{128} \times 2^{64} \times 2^{32} \times 2^8 \times 2^1 \equiv6 \times 2 \equiv 2(\mod 10)\)；
\(\prod p_i^{a_i} \equiv 1( \mod 10)\)
故原式结果为 \(2 \times 10^{249}\)。