前缀和、差分、树状数组的应用
树状数组
树状数组的原理,今天终于弄懂了:
https://www.bilibili.com/video/BV1ce411u7qP/?spm_id_from=333.337.search-card.all.click
考虑线段树: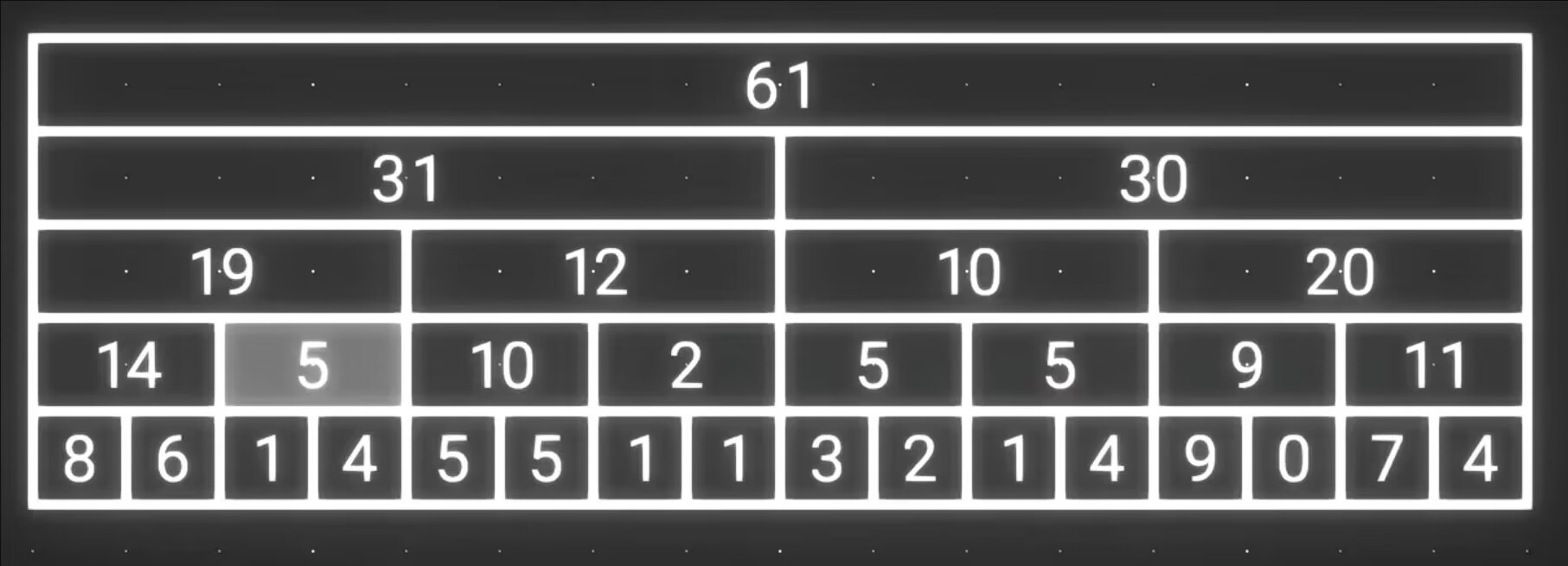
当我们只需要求前缀和的时候,有一些区间是没有用的,例如这个 \(5\)。于是我们把他们去掉之后,剩下的区间正好有 \(n\) 个:
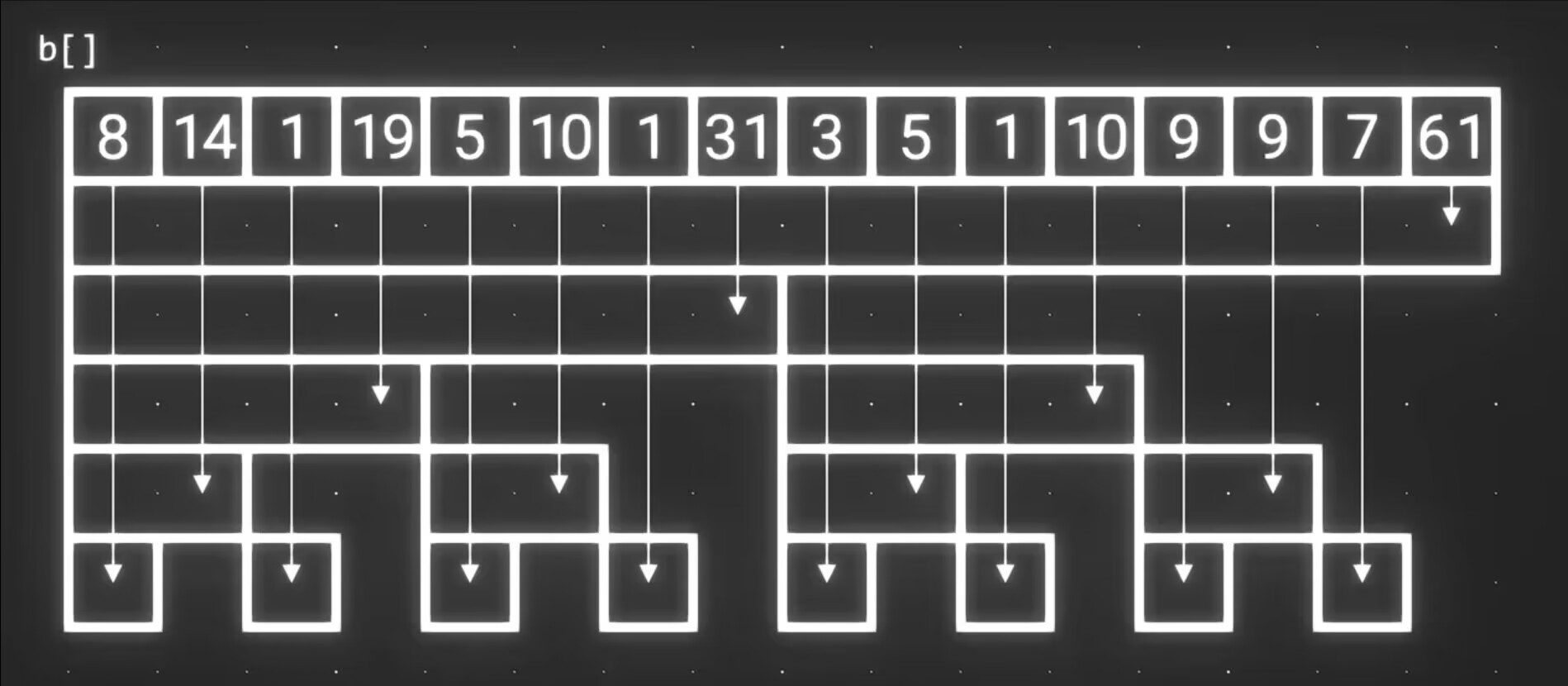
其中每一个区间的长度都是它的代表元素的 lowbit。
也就是用功能换空间,放弃了任意区间用加法方式求区间和的功能,把空间从 \(O(n \log n)\) 优化到 \(O(n)\)。
值得注意的是,虽然可以用差分的方式在同样的时间内求出区间和,但是这对于一些没有逆操作的情形并不适用。例如区间矩阵积,由于矩阵不一定有逆,所以不能用树状数组维护,只能用线段树。
二维差分
铁律:差分的前缀和数组是原数组。
由一维差分的应用(将区间加改为单点加操作)我们可以扩展到二维差分的应用,就是把将矩阵的 \((a,b)\) 到 \((c,d)\) 的区块加改为四个点的加操作。
即:\(D[a,b]+=delta; D[c+1,b]-=delta; D[a,d+1]-=delta; D[c+1, d+1] += delta\)。
看图理解:(若原数组一个方块 \(+delta\),其前缀和数组中右下的每一个方块都会 \(+delta\)。)

讲完修改操作,但问题是先得有一个矩阵啊!怎么构造呢?我们这里使用的方法是插入法。
假设原矩阵为 \(\{0\}\),那么差分矩阵也为 \(\{0\}\)。然后按顺序(不影响的顺序,就是从左到右从上到下)对每一个点 \((i,j)\) 都进行插入操作:\(\operatorname{insert}(i, j),(i, j)\)。
要输出原数组的时候,只需要进行一次二位前缀和即可。
例题:https://www.luogu.com.cn/problem/P4514
(这个题目,光用这个还过不去(\(query\) 操作的时间是 \(O(qnm)\)),需要使用二维树状数组优化前缀和的计算时间复杂度。)
\(O(qnm)\) 代码:
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int n, m;
int D[2050][2050], A[2050][2050], s[2050][2050];
/*
L a b c d delta —— 代表将 (a,b),(c,d)(a,b),(c,d) 为顶点的矩形区域内的所有数字加上 deltadelta。
k a b c d —— 代表求 (a,b),(c,d)(a,b),(c,d) 为顶点的矩形区域内所有数字的和。
*/
void insert(int a, int b, int c, int d, int delta) {
D[a][b] += delta; D[c + 1][b] -= delta;
D[a][d + 1] -= delta; D[c + 1][d + 1] += delta;
}
void query(int a, int b, int c, int d) {
//求出原数组
f(i, 1, n)
f(j, 1, m)
A[i][j] = A[i - 1][j] + A[i][j - 1] - A[i - 1][j - 1] + D[i][j];
f(i, 1, n)
f(j, 1, m)
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + A[i][j];
cout << s[c][d] - s[a - 1][d] - s[c][b - 1] + s[a - 1][b - 1] << endl;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
char op; cin >> op;
cin >> n >> m;
/*若有初始值
f(i, 1, n)
f(j, 1, m)
insert(i, j, i, j, a[i][j]);*/
while(cin >> op && op != EOF) {
if(op == 'L') {
int a, b, c, d, delta; cin >> a >> b >> c >> d >> delta;
insert(a, b, c, d, delta);
}
else {
int a, b, c, d; cin >> a >> b >> c >> d;
query(a, b, c, d);
}
}
return 0;
}
树状数组统计差分数组形式下原数组的前缀和
假设有一个数组 \(A\),我们只维护它的差分数组 \(D\),有 \(q\) 次 \(D\) 的单点修改操作(也就是 \(A\) 的区间加操作)。要求前缀和数组 \(S\)。暴力解法是对于每一个 \(q\) 做一次前缀和,时间复杂度 \(O(qn)\)。
我们考虑分解:
\(A[1] = D[1];\)
\(A[2] = D[1] + D[2];\)
\(A[3] = D[1] + D[2] + D[3];\)
\(A[4] = D[1] + D[2] + D[3] + D[4];\)
考虑统计 \(D[x]\) 出现的次数,那么 \(S[4]=\sum\limits_{i = 1}^{4} A_i\)
\(~~~~~~=4D[1] + 3D[2] + 2D[3] + D[4]\)
\(~~~~~~=5(D[1] + D[2] + D[3] + D[4]) - (D[1] + 2D[2] + 3D[3] + 4D[4])\)。
化为第三步的时候,应该可以看出来了:这个东西可以通过维护 \(D[x]\) 和 \(xD[x]\) 的前缀和求出。(第二步的形式,系数是不随统计的末位置 \(i\) 固定的,我们需要把系数变形成固定的)
暴力维护前缀和,时间复杂度没有优化,为 \(O(qn)\)。但使用树状数组维护前缀和,可以将时间复杂度优化至 \(O(q \log n)\)。
这就是树状数组的区间修改,区间查询。
(区间修改,单点查询的话,比如要维护一个序列,每次给 \(l-r\) 加上 \(k\)。依然使用差分数组,并将差分树状数组中做 \(l\) 的单点加 \(k\) 操作,做 \(r+1\) 的单点减 \(k\) 操作。然后查询时求前缀和即可)
例题:https://www.luogu.com.cn/problem/P3372
AC 代码:
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int n, m;
ll d[100010], id[100010], a[100010];
ll di[100010], idi[100010];
int lowbit(int x) {
return x & -x;
}
void add(int x, int k, int tnum) {
if(tnum == 1) {
//add di
while(x <= n) {
di[x] += k;
x += lowbit(x);
}
}
else {
//add idi
while(x <= n) {
idi[x] += k;
x += lowbit(x);
}
}
}
ll query(int x, int tnum) {
ll ans = 0;
if(tnum == 1) {
//add di
while(x > 0) {
ans += di[x];
x -= lowbit(x);
}
}
else {
//add idi
while(x > 0) {
ans += idi[x];
x -= lowbit(x);
}
}
return ans;
}
ll s(ll x) {
return (x + 1) * query(x, 1) - query(x, 2);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
f(i, 1, n) {
cin >> a[i]; d[i] = a[i] - a[i - 1]; id[i] = d[i] * i;
add(i, d[i], 1); add(i, id[i], 2);
}
//1 x y k:将区间 [x, y][x,y] 内每个数加上 kk。
//2 x y:输出区间 [x, y][x,y] 内每个数的和。
f(i, 1, m) {
int op; cin >> op;
if(op == 1) {
int x, y, k; cin >> x >> y >> k;
add(x, k, 1); add(y + 1, -k, 1);
add(x, x * k, 2); add(y + 1, -(y + 1) * k, 2);
}
else {
int x, y; cin >> x >> y;
cout << s(y) - s(x - 1) << endl;
}
}
return 0;
}
推广到二维情况怎么做?
依然借鉴前面的方法,将 \(S[a][b]\) 表示出来:
\(\sum\limits_{i = 1}^{a} \sum\limits_{j = 1}^{b}\sum\limits_{x = 1}^{i}\sum\limits_{y = 1}^{j} D[x][y]\)
依然举例子,统计 \(d[x][y]\) 的出现次数:
\(S[2][3] = A[1][1] + A[1][2] + A[1][3] + A[2][1] + A[2][2] + A[2][3]\)
\(A[1][1] = D[1][1]\)
\(A[1][2] = D[1][1] + D[1][2]\)
\(A[1][3] = D[1][1] + D[1][2] + D[1][3]\)
\(A[2][1] = D[1][1] + D[2][1]\)
\(A[2][2] = D[1][1] + D[1][2] + D[2][1] + D[2][2]\)
\(A[2][3] = D[1][1] + D[1][2] + D[1][3] + D[2][1] + D[2][2] + D[2][3]\)
可以发现,\(D[x][y]\) 会统计 \((a-x+1) \times (b-y+1)\) 次。
那么 \(S[a][b] = \sum\limits_{i = 1}^{a} \sum\limits_{j = 1}^{b} (a-i+1)(b-j+1)D[i][j]\)
\(~~~~~~~~~~~~~~~~~~=\sum\limits_{i = 1}^{a} \sum\limits_{j = 1}^{b} ij D[i][j] + (-b-1)iD[i][j] + (-a-1)jD[i][j] + (ab+a+b+1)D[i][j]\)
可以使用树状数组维护。
维护过程中,四个树状数组最好合在一起维护,因为分开会错。这是 AC 代码:
#include<bits/stdc++.h>
using namespace std;
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int n, m;
int td[2050][2050], tdi[2050][2050], tdj[2050][2050], tdij[2050][2050];
/*
L a b c d delta —— 代表将 (a,b),(c,d)(a,b),(c,d) 为顶点的矩形区域内的所有数字加上 deltadelta。
k a b c d —— 代表求 (a,b),(c,d)(a,b),(c,d) 为顶点的矩形区域内所有数字的和。
*/
int lowbit(int x) {
return x & (-x);
}
void add(int x, int y, int k) {
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
{
td[i][j]+=k;
tdi[i][j]+=k*x;
tdj[i][j]+=k*y;
tdij[i][j]+=k*x*y;
}
}
void insert(int a, int b, int c, int d, int delta) {
add(a, b, delta);
add(a, d + 1, -delta);
add(c + 1, b, -delta);
add(c + 1, d + 1, delta);
}
int query(int x, int y) {
int ans = 0;
for(int i=x;i;i-=lowbit(i))
for(int j=y;j;j-=lowbit(j))
ans+=((x+1)*(y+1)* td[i][j]-(y+1)*tdi[i][j]-(x+1)*tdj[i][j]+tdij[i][j]);
return ans;
}
void q(int a, int b, int c, int d) {
cout << query(c, d) - query(a - 1, d) - query(c, b - 1) + query(a - 1, b - 1) << endl;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
char op;
cin >> op;
cin >> n >> m;
while(cin >> op && op != EOF) {
if(op == 'L') {
int a, b, c, d, delta; cin >> a >> b >> c >> d >> delta;
insert(a, b, c, d, delta);
}
else {
int a, b, c, d; cin >> a >> b >> c >> d;
q(a, b, c, d);
}
}
return 0;
}
维护有函数关系下标的前缀和
ABC265F
\(dp_{i,j,k}\) 表示前 \(i\) 维,和 \(p\) 的距离是 \(j\),和 \(q\) 的距离是 \(k\) 的方案数。
转移:\(dp_{i,j,k} = \sum \limits_{(s_1,s_2)} dp_{i-1,j-s_1, k-s_2}\),其中 \(s_1\) 和 \(s_2\) 是任选 \(r_i\) 的时候 \(r_i\) 分别和 \(p_i\) 和 \(q_i\) 的距离。这样是 \(O(nd^3)\) 的,过不去。
(插播)明确目标很重要,我在做题的时候没有明确应该从 \(dp_{i-1,j',k'}\) 转移而来这个目标,去推了什么 \(s_1,s_2\);\(j-s_1,k-s_2\)(虽然这个是对的但是我当时不太清楚自己在推什么也没啥用) 的性质啥的,迷茫了好久。
然后发现一个重要性质,能转移到的 \(s_1\) 和 \(s_2\) 有以下三种可能:(设 \(|p_i - q_i| = t\))
- \(s_1 \in [0,d-t], s_2 = s_1 + t\)
- \(s_1 \in [0,t], s_2 = t - s_1\)
- \(s_1 \in [t,d], s_2 = s_1 - t\)
可以发现有几个一次函数关系,任意一条一次函数的横坐标在 \([0,x]\) 的权值的前缀和可以记录 \(k,b,x\) 三维来维护。但是这里的 \(k\) 只有 \(-1,1\) 两种,所以 \(s\) 的空间是 \(O(d^2)\) 的。
当然我们需要的还是 \(j,k\) 能转移到的 \(j'\) 和 \(k'\) 的性质。这个也可以推,挺复杂的,看代码。但是注意不存在的区间一定要判掉,不能让他倒减前缀和了,这个东西在 extra-test 里卡了我两次。
(写的时候全是细节)
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int mod = 998244353;
const int inf = 1e9;
int p[110], q[110];
int dp[110][1010][1010];
const int o = 2002;
int s[2][4010][3010];
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n, d; cin >> n >> d;
f(i, 1, n) cin >> p[i]; f(i, 1, n) cin >> q[i];
int ans = 0;
dp[0][0][0] = 1;
f(i, 0, d) s[0][o][i] = s[1][o][i] = 1;
f(i, 1, n) {
int t = llabs(q[i] - p[i]);
f(j, 0, d) f(k, 0, d) {
if(j - t >= 0)dp[i][j][k] += s[1][o+k-j+t][j-t] - (j-k-t-1<0?0:s[1][o+k-j+t][j-k-t-1]);
if(j > 0 && t != 0)dp[i][j][k] += s[0][o+j-t+k][j-1] - (j-t<0?0:s[0][o+j-t+k][j-t]);
if(j >= 0 && j >= j + t - k)dp[i][j][k] += s[1][o+k-t-j][j] - (j+t-k-1<0?0:s[1][o+k-t-j][j+t-k-1]);
if(t == 0)dp[i][j][k] -= dp[i-1][j][k];
dp[i][j][k] = ((dp[i][j][k] % mod) + mod) % mod;
}
memset(s, 0, sizeof(s));
f(j, 0, d) f(k, 0, d) {
s[1][o+k-j][j] += dp[i][j][k];
s[0][o+k+j][j] += dp[i][j][k];
}
f(j, 0, o+d+d) f(k, 1, d) {
// cout << j << " " << k << " " <<
s[0][j][k] = s[0][j][k-1] + s[0][j][k];
s[1][j][k] = s[1][j][k-1] + s[1][j][k];
s[0][j][k] %= mod; s[1][j][k] %= mod;
}
}
f(j, 0, d) f(k, 0, d) {
ans += dp[n][j][k];
ans %= mod;
}
cout << ans << endl;
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
树上差分
树上差分可以将链式修改用单点修改代替。(可能也有别的用途,但是链式修改最常见,可以灵活机动)
定义树上前缀和式子(其中 \(a_i\) 是我们实际上要维护的东西):
也就是子树上的权值和。
倒着推一下,得到树上差分递推式子:
让我们看看在链上的表现吧!

假设我们有 \(n\) 个点,并且有 \(q\) 个询问,每个询问形如:给 \(7-8\) 这条链上每个点 \(+1\)。
对于 \(4\),自己 \(+1\),儿子们总共 \(+2\),那么 \(d_4 \leftarrow d_4 - 1\)。
对于 \(7,8\),自己 \(+1\),儿子们总共 \(+0\),那么 \(d_7 \leftarrow d_7 + 1\),\(8\) 同理。
对于 \(1\),自己 \(+0\),儿子们总共 \(+1\),那么 \(d_1 \leftarrow d_1 - 1\)
对于其他节点,自己 \(+1\),儿子们总共 \(+1\),不需要改动!
我们只需要改动四次。那么总时间复杂度是 \(O(n + q\log n)\),其中 \(\log n\) 来自 LCA。
di[x]++; di[y]++; di[lca(x,y)]--; di[anc[lca(x,y)][0]]--;
(这里 \(1\) 是根,实际上无根树也可以这么做。)
P3128
模板题
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
vector<int> g[50010];
int di[50010];
int dep[50010];
int anc[50010][30]; //i 的第 2^j 个父亲是谁
void dfs(int now, int fa) {
dep[now] = dep[fa] + 1;
anc[now][0] = fa;
int len = log2(dep[now]);
f(i, 1, len) {
anc[now][i] = anc[anc[now][i - 1]][i - 1];
}
f(i, 0, (int)g[now].size() - 1) {
if(g[now][i] != fa) {
dfs(g[now][i], now);
}
}
}
int lca(int x, int y) {
if(dep[x] < dep[y]) swap(x, y);
int d = dep[x] - dep[y];
if(d > 0) {
int len = log2(d);
f(i, 0, len) {
if((d >> i) & 1) {
x = anc[x][i];
}
}
}
if(x == y) return x;
int lenn = log2(dep[y]);
for(int i = lenn; i >= 0; i--) {
if(anc[x][i] != anc[y][i]) {
x = anc[x][i], y = anc[y][i];
}
}
return anc[y][0];
}
int ans[50010];
void dfs2(int now, int fa){
f(i, 0, (int)g[now].size() - 1) {
if(g[now][i] != fa) {
dfs2(g[now][i], now);
ans[now] += ans[g[now][i]];
}
}
ans[now] += di[now];
return;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int n, k; cin >> n >> k;
f(i, 1, n - 1) {
int x, y; cin >> x >> y;
g[x].push_back(y); g[y].push_back(x);
}
dfs(1, 0);
f(i, 1, k) {
int x, y; cin >> x >> y;
di[x]++; di[y]++; di[lca(x,y)]--; di[anc[lca(x,y)][0]]--;
}
dfs2(1, 0);
int ret = 0;
f(i, 1, n) ret = max(ret, ans[i]);
cout << ret << endl;
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
P9202 「GMOI R2-T2」猫耳小(加强版)
只是想讲一个做蠢了的地方。
有一些点 +1/-1,多次询问 \([1, k]\) 中 \(>0\) 的位置个数。
这个我用了树状数组,实际上根本没必要。这个询问是零维度的,只需要直接记录 cnt 即可。

