图论杂题
ABC270F
https://atcoder.jp/contests/abc270/tasks/abc270_f
题意:有 \(n\) 个岛屿,初始空空如也。可以进行若干次如下操作中的一个:
- 在第 \(i\) 个岛屿上建立一个飞机场并花费 \(a_i\) 的代价。
- 在第 \(i\) 个岛屿上建立一个码头并花费 \(b_i\) 的代价。
- 对于给定的若干个二元组 \((u,v)\) 中选择一个 \((u_i,v_i)\),在 \(u_i\) 和 \(v_i\) 之间建造一条双向道路,并话费 \(c_i\) 的代价。
拥有飞机场的岛屿之间可以相互通行;拥有码头的岛屿之间可以相互通行。
求使得这 \(n\) 个岛屿联通的最小代价。
分析:这个题目上次在睿爸那里做过一道,当时没有开放补题通道就没有整理。这次又遇到还是不会做。这不太行啊。
我们转化题意,看看按照上述方法建图,连通性实际上是怎么样。建立虚点 \(n+1\) 和 \(n+2\);建立飞机场的点当作 \(i\) 和 \(n+1\) 的边,边权为 \(a_i\);码头则是 \(i\) 和 \(n+2\) 的边,边权为 \(b_i\)。这样只要求使得 \(1 \sim n\) 连通的最小生成树即可(不要求 \(n+1\) 和 \(n+2\) 连通)。
具体实现就进行四次最小生成树,分别要求 \(1 \sim n\);\(1 \sim n+1\);\(1 \sim n\) 和 \(n+2\);\(1 \sim n+2\) 连通,并且只使用 \({c}\);\(a,c\);\(b,c\);\(a,b,c\) 之间的边。然后再求最小生成树边权之间的最小值即可。
ARC150C
题意:给定 \(n\) 点 \(m\) 边无向连通图 \(G\) 和数组 \(A_{1,...,n},B_{1,...,k}\),判断是否有如下性质:
- 对于所有从 \(1\) 到 \(n\) 的简单路径 \(\{v_1,v_2,...,v_j\}(v_1 = 1, v_j = n)\),\(B\) 是 \(A_{v_1},A_{v_2},...A_{v_j}\) 的(不必要连续的)子序列。
分析:这是一个可以学习的新型套路:如果遇到“所有”的路径(不一定是简单路径)那么考虑转化为最短路问题,令 \(w_i\) 为从 \(1\) 走到 \(i\) 的路径中只要经过下一层的点就一定将其与 \(b\) 的下一层匹配,能匹配到的点的最小值(类似数学里的“任意”就要求出最劣的点然后看是否满足条件)。然后看 \(w_n\) 是否等于 \(k\) 即可。这个用 dijkstra 实现不难。(在这道题里不依赖于简单路径,可以有环)
赛时想到建立圆方树,但是首先这个 \(b\) 里可能有重复的元素没有办法将整张图分层;其次点双连通分量中每两个点只是“有两条以上简单路径”而不知道具体是多少,于是不可做。
地铁换乘
https://oj-szshs.bopufund.com/p/44?tid=634a4cb48ce73726d6d08d5f
题意:给定 \(n\) 点 \(m\) 边地铁图,第 \(i\) 条边表示连接两个站的 \(c_i\) 号线地铁,花费为 \(t_i\)。在一个站点可以换乘,从第 \(i\) 号线换到第 \(j\) 号线,花费 \(|x - y|\) 的时间。求从 \(1\) 号站点到达每个站点的最短时间。
分析:这道题利用的是拆点的思路,把每个地铁所拥有的颜色都建一个点,然后颜色与颜色之间建 \(|x-y|\) 的边,然后把所有 \(1\) 的某一个颜色的 \(dis\) 设为 \(0\),跑 dijkstra 即可。
注意实现细节,特别是没有边的时候 \(dis_1 = 0\)。
CF1749E
题意:Monocarp正在玩Minecraft,他想建造一堵仙人掌墙。他想在一块大小为n×m单元的沙地上建造它。最初,场地的一些单元里有仙人掌。请注意,在Minecraft中,两个仙人掌不能生长在相邻的单元格上——而初始场地符合这一限制。Monocarp可以种植新的仙人掌(它们也必须满足前述条件)。他不能砍掉已经长在田地上的任何仙人掌——他没有斧头,而且仙人掌对他的手来说太扎手了。
莫诺卡普认为,如果从田地的最上面一排到最下面一排没有路径,那么这堵墙就是完整的。
路径上的每两个连续单元都是相邻的。
属于该路径的单元格中没有仙人掌。
你的任务是种植最小数量的仙人掌来建造一堵墙(或报告说这是不可能的)。
\(n,m \le 2 \times 10^5, \sum nm \le 4 \times 10^5\)
分析:
又是 dijkstra。
我们抽象出模型,需要做的是构造一条从左到右的路。
然后一条路上的点 \(i+j\) 奇偶性完全相同。
左边是起点,右边是终点,边权是是否要建造仙人掌。
点数 \(\le 2 \times 10^5\),边数 \(\le 8 \times 10^5\)。
能过。
实现:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
int n, m;
vector<vector<char>> c;
priority_queue<pair<int, pair<pii,pii>>> q; //-dis, cur, lst
vector<vector<int>> dis;
vector<vector<bool>> vis;
vector<vector<pii>> lst;
int dx[]={1,-1,0,0};
int dy[]={0,0,1,-1};
int ddx[]={1,1,-1,-1};
int ddy[]={-1,1,-1,1};
int ans=inf, cho;
bool ok(int x,int y){
f(i,0,3){
int nx=x+dx[i],ny=y+dy[i];
if(nx<0||nx>n||ny<0||ny>m)continue;
if(c[nx][ny]=='#')return 0;
}
return 1;
}
void dijkstra() {
while(!q.empty()) {
int d=-q.top().first;
pii cur=q.top().second.first,las=q.top().second.second;
q.pop();
if(vis[cur.first][cur.second])continue;
vis[cur.first][cur.second]=1;
dis[cur.first][cur.second]=d;
lst[cur.first][cur.second]=las;
int x=cur.first,y=cur.second;
f(i,0,3){
int nx=x+ddx[i],ny=y+ddy[i];
if(nx<1||nx>n||ny<1||ny>m)continue;
if(ok(nx,ny)){
if(c[nx][ny]=='#') q.push({-d,{{nx,ny},cur}});
else q.push({-(d+1),{{nx,ny},cur}});
}
}
}
f(i,1,n){
if(ans>dis[i][m]){
ans=min(ans,dis[i][m]); cho=i;
}
}
//找不到
return;
}
void walk(int x, int y) {
if(x == 0 && y == 0) return;
c[x][y]='#';
walk(lst[x][y].first,lst[x][y].second);
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
time_t start = clock();
//think twice,code once.
//think once,debug forever.
int T; cin >> T;
while(T--) {
ans=inf;
cin>>n>>m;
c.resize(n+5);
f(i,0,n+1)c[i].resize(m+5);
vis.resize(n+5);
f(i,0,n+1)vis[i].resize(m+5);
lst.resize(n+5);
f(i,0,n+1)lst[i].resize(m+5);
dis.resize(n+5);
f(i,0,n+1)dis[i].resize(m+5);
f(i,1,n)f(j,1,m)dis[i][j]=inf;
f(i,1,n)f(j,1,m)vis[i][j]=0;
f(i,1,n)f(j,1,m)cin>>c[i][j];
//处理 i+j 为奇数的
for(int i=1;i<=n;i+=2){
if(ok(i,1)) {
q.push({-(c[i][1]=='.'), {{i,1},{0,0}}});
}
}
dijkstra();
f(i,1,n)f(j,1,m)dis[i][j]=inf;
f(i,1,n)f(j,1,m)vis[i][j]=0;
for(int i=2;i<=n;i+=2){
if(ok(i,1)) {
q.push({-(c[i][1]=='.'), {{i,1},{0,0}}});
}
}
dijkstra();
if(ans==inf)cout<<"NO\n";
else {
cout<<"YES\n";
walk(cho,m);
f(i,1,n){f(j,1,m)cout<<c[i][j];cout<<endl;}
}
}
time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
CF1737D
敲头,上次没补明白这次还不会!
【题意】
有一个包含 \(n\) 个点和 \(m\) 条边的无向图,每条边 \(i\) 连接着点 \(u_i\) 和 \(v_i\),权值为 \(w_i\),通过这条边要用 \(w_i\) 微秒。
Ela 需要从 \(1\) 号点走到 \(n\) 号点,但他觉得原本的路径太长了。好在,Wiring Wizard 可以帮他改变路径。
具体地,对于任意三点 \(u,v,t\)(\(u\) 和 \(t\) 可以相同),若 \(u\) 与 \(v\) 之间有边 \(i\),且 \(v\) 与 \(t\) 有边 \(j\),那么他可以用 \(w_i\) 微秒断开边 \(i\),并且在 \(u\) 与 \(t\) 之间连一条权值为 \(w_i\) 的边。他可以改任意条边,也可以不改。
Ela 想知道,他至少要花多久时间才能从 \(1\) 号点走到 \(n\) 号点(时间包括修改边的时间)。
有 \(t\) 组数据。
\(1\le t\le 100\)
\(2\le n\le 500\ ,\ n-1\le m\le 250000\)
\(1\le u_i,v_i\le n\ ,\ 1\le w_i\le 10^9\)
\(\Sigma{n}\le 500\ ,\ \Sigma{m}\le 250000\)
保证输入的图为联通图,无自环,但可能有重边。
【分析】
首先观察到如果某一条路径上有 \(a_1,...,a_k\) 这些点,那么缩成 \(k \times \min \limits_{i = 1}^ k a_i\) 是最佳选项。
然后考虑能不能推到每一条边上(也就是是否有结论:答案一定等于某条边的边权乘以某个数)。考虑这张图:
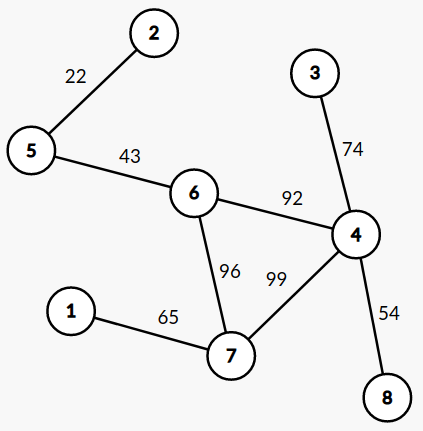
假设最后走了若干条边 \(b_1,b_2,..,b_k\)。那么规约到上个引理。因此我们最后只会走一条边。假设这条边的边权是 \(t\)。
考虑它和其他边合并的过程。如果遇到比它大的边,那么使用这条边权还不如使用自己。否则,可以直接继续用小边,不会用到自己。
因此我们证明了,答案一定等于某条边的边权乘以某个数。
依然考虑上述图,是做了七次操作,如下图:
发现是先将一个节点移到一条 \(1\) 到 \(n\) 的路径上,然后另一个节点拉到一起做一个自环,然后两边拉伸。考虑做自环的点的编号为 \(k\),先移动的节点是 \(u\)。那么答案为 \(w \times (dis_{1,k} + dis_{k, n} + dis_{u, k} + 1 + 1)\)。值得注意的是,这个 \(dis\) 都是不包含原边的。但是没关系。如果只有走这条边才能到达 \(k\),那么 \(k\) 一定非最佳选择。(因为 \(dis_{1,k}+dis_{k,n}\) 太大)
但是有个特例:如果本身就是 \(1 \sim n\) 上的某一条路径上的一条边,那么不用做自环,直接就可以进行伸展。对于这部分的答案,我们抽象出来:
定义一条由若干条边组成的路径的距离为 (这个路径上边权最小值 × 走过的边数)。求 \(1 \sim n\) 的最短距离。
dijkstra 是不行的,不符合贪心性质。应该怎么办?考虑固定最小那条边,然后用边的两头的 distance 计算。这个显然正确。那么总复杂度 \(O(nm)\)。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e14;
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
vector<int> num[550][550];
int mn[550][550];
int dis[550][550];int n,m,ans;
void floyd() {
f(k,1,n)f(i,1,n)f(j,1,n){
cmin(dis[i][j],dis[i][k]+dis[k][j]);
}
}
struct edge{
int u,v,w;
}e[250010];
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
int T; cin >> T;
while(T--) {
cin>>n>>m;
f(i,1,n)f(j,1,n)num[i][j].clear();
f(i,1,n)f(j,1,n)mn[i][j]=inf;
f(i,1,m){
int u,v,w;cin>>u>>v>>w;
num[u][v].push_back(w);
num[v][u].push_back(w);
cmin(mn[u][v],w);
cmin(mn[v][u],w);
e[i]=(edge){u,v,w};
}
f(i,1,n)f(j,1,n){
if(i==j)dis[i][j]=0;
else if(num[i][j].empty())dis[i][j]=inf;
else dis[i][j]=1;
}
floyd();
ans=inf;
f(i,1,n)f(j,1,n){
cmin(ans, mn[i][j] * (dis[1][i] + dis[j][n] + 1));
}
f(i,1,m){
int u=e[i].u,v=e[i].v,w=e[i].w;
f(k,1,n){
int xx=min(dis[u][k],dis[v][k]);
cmin(ans,w*(xx+1+dis[1][k]+dis[k][n]+1));
}
}
cout<<ans<<endl;
}
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
JOI2023 C
【题意】
给定一个 \(n \times m\) 的 \(01\) 网格,有一个 \(k \times k\) 的印章,可以花费 \(1\) 的代价盖在任何一个地方并把这些格子都变成 \(0\)。求使得起点和终点之间有一条只由 \(0\) 组成的边花费的最小代价。
考虑正解: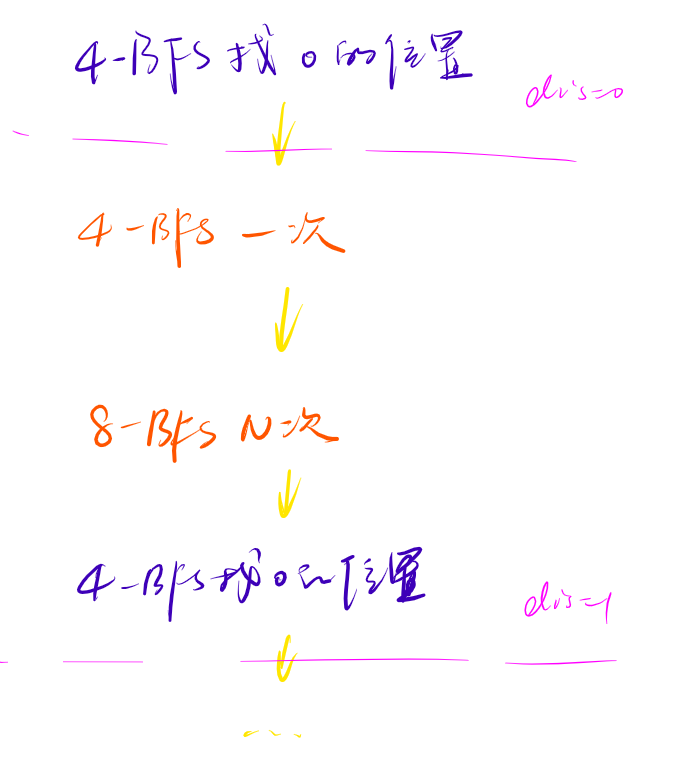
这么一个流程,我们怎么实现能够不退化地完成这个 01-BFS 呢?
先看代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define f(i, a, b) for(int i = (a); i <= (b); i++)
#define cl(i, n) i.clear(),i.resize(n);
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int inf = 1e9;
//#define cerr if(false)cerr
//#define freopen if(false)freopen
#define watch(x) cerr << (#x) << ' '<<'i'<<'s'<<' ' << x << endl
void pofe(int number, int bitnum) {
string s; f(i, 0, bitnum) {s += char(number & 1) + '0'; number >>= 1; }
reverse(s.begin(), s.end()); cerr << s << endl;
return;
}
void cmax(int &x, int y) {if(x < y) x = y;}
void cmin(int &x, int y) {if(x > y) x = y;}
//调不出来给我对拍!
struct node{int r,c;}s,g;
bool in(int x,int l,int r){return x>=l&&x<=r;}
int r,c,n; bool ok(int x,int y){return in(x,1,r)&&in(y,1,c);}
deque<tuple<int,int,int,int>> q;
vector<vector<int>> a,d;
int dx[]={0,0,-1,1,-1,1,-1,1};
int dy[]={-1,1,0,0,1,1,-1,-1};
signed main() {
ios::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
//freopen();
//freopen();
//time_t start = clock();
//think twice,code once.
//think once,debug forever.
cin>>r>>c>>n; a.resize(r+10),d.resize(r+10);
f(i,1,r)a[i].resize(c+10),d[i].resize(c+10);
cin>>s.r>>s.c>>g.r>>g.c;
f(i,1,r)
f(j,1,c){
char ch;cin>>ch; a[i][j]=(ch=='#'?1:0),d[i][j]=inf;
}
q.push_back({0,n,s.r,s.c}); //return 0;
while(d[g.r][g.c]==inf){
auto [i,j,k,l] = q.front();
q.pop_front();
if(d[k][l] != inf) continue;
d[k][l] = i;//cout <<k<<" "<<l<<" "<<d[k][l]<<endl;
if(j < n) {
f(t, 0, 7) {
if(!ok(k+dx[t],l+dy[t]))continue;
q.push_back({i,j+1,k+dx[t],l+dy[t]});
}
}
else {
f(t, 0, 3) {
if(!ok(k+dx[t],l+dy[t]))continue;
if(a[k+dx[t]][l+dy[t]]==0){
q.push_front({i,j,k+dx[t],l+dy[t]});
}
else {
q.push_back({i+1,1,k+dx[t],l+dy[t]});
}
}
}
}
cout<<d[g.r][g.c]<<endl;
//time_t finish = clock();
//cout << "time used:" << (finish-start) * 1.0 / CLOCKS_PER_SEC <<"s"<< endl;
return 0;
}
/*
2023/x/xx
start thinking at h:mm
start coding at h:mm
finish debugging at h:mm
*/
(注意,auto [i,j,k,l] = ... 这个东西是 c++17 的,ccf 是不能用的。)
主要就是,考虑记录层数和其距离。
首先,不会出现一个点被遍历两次依然有效的情况。证明和 bfs 的证明是差不多的(前提是第一次的时候以步数为第一关键字,层数为第二关键字是最小的):考虑该位置可以拓展到什么位置。显然步数相同的时候,层数更小的可以覆盖层数更大的范围。步数不同的时候,可以先走若干步到步数相同的时候,显然更是能覆盖了。因此一个点不会有两次有用。
其次,01bfs 的时候其实也是以步数为第一关键字,层数为第二关键字分层。这就代表了,我们步数增加的时候也要放到队尾。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号