https://www.luogu.com.cn/problem/P6795
我一直很注重思考过程。这是做题的根本。
初看 T3，一个比较显然的贪心思路是，向外扩张合并连续段。
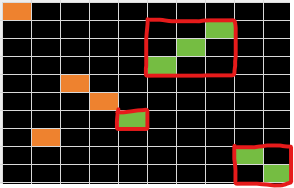
由此清晰地发现，从 1 到 N，被左边的数切分成若干“剩余”连续段，连续段内部，在右边的排列一定是连续的，右边的答案实际上已经确定。
并且这些连续段的延伸方向一定是由内向外。
关键在于如何对待跨越左边和右边的连续段，它决定了我们如何排列右边的“剩余”连续段。我们有必要考虑左边右边如何贡献。
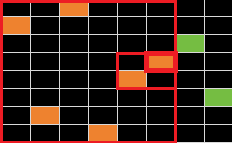
对左边而言，当且仅当红框位置能贡献。形式化地说，记 a 离散化后的数组为 b，当且仅当 b[p~K] 是连续段，p 能作为左端点贡献。
取出所有 b[p~K]，它们代表的值域区间从右到左记为 [li,ri]。
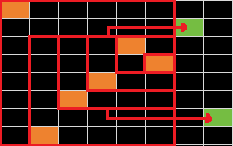
当一个端点变化时，一定是要加入当中的连续段的。比如下面那个绿块。
但是恰在变化之前，有一段端点不变的时间，这段时间内加入是任意的。比如上面那个绿块，它不是恰好变化时加入的，而是在下面那个绿块加入前加入的。
什么时候加入最优？我们有必要计算一个时刻 [li,ri] 加入的贡献。比如，假设此时有一些 l 不变的连续段，考虑加入小于 l 的一些绿块。显然，这些绿块中，每个绿块贡献相同。
（参考 DaiRuiChen007）
如果当前在这些 l 不变的连续段中的第一个，贡献无疑是 1。
否则，如果上一个连续段的右端点与当前右端点间，没有应加入的绿块，贡献为上一个加一。
否则，若只有一段应加入的绿块，贡献为 2，否则为 1。
算出哪个地方加入最优后，构造是自然的。
你可能要问一个时刻左右端点都有任务怎么办。答案是先加入贡献更大的。证明：贡献小的端点（的贡献位置）一定是贡献大的端点的子集。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cstdlib>
#define fi first
#define se second
#define mkp std::make_pair
using ll=long long;
using std::max;
using std::min;
template<class T> void cmax(T&a,T adic){a=max(a,adic);}
template<class T> void cmin(T&a,T adic){a=min(a,adic);}
const int NV=2e5;
namespace seg{
struct SEGN{
int mn,mnc,tad;
} tr[NV*4+5];
void doadd(int x,int z){
tr[x].mn+=z;
tr[x].tad+=z;
}void dn(int x){
if(tr[x].tad){
doadd(x*2,tr[x].tad);
doadd(x*2+1,tr[x].tad);
tr[x].tad=0;
}
}void up(int x){
tr[x].mn=min(tr[x*2].mn,tr[x*2+1].mn);
tr[x].mnc=0;
if(tr[x].mn==tr[x*2].mn) tr[x].mnc+=tr[x*2].mnc;
if(tr[x].mn==tr[x*2+1].mn) tr[x].mnc+=tr[x*2+1].mnc;
}void add(int x,int l,int r,int ql,int qr,int z){
if(ql<=l&&r<=qr) return doadd(x,z);
int mid=l+r>>1;
dn(x);
if(ql<=mid) add(x*2,l,mid,ql,qr,z);
if(mid<qr) add(x*2+1,mid+1,r,ql,qr,z);
up(x);
}void build(int x,int l,int r){
int mid=l+r>>1;
tr[x].mn=0;
tr[x].tad=0;
tr[x].mnc=r-l+1;
if(l!=r){
build(x*2,l,mid);
build(x*2+1,mid+1,r);
}
}
}
namespace xm{
int N,K,a[NV+5],adic[NV+5],stmx[NV+5],stmn[NV+5],\
bli[NV+5],bl[NV+5],br[NV+5],rk[NV+5],\
vl[NV+5],vr[NV+5],vpl[NV+5],vpr[NV+5];
void _(){
scanf("%d%d",&N,&K);
for(int i=1;i<=K;++i){
scanf("%d",a+i);
adic[i]=a[i];
}
std::sort(adic+1,adic+K+1);
adic[K+1]=N+1;
for(int i=1;i<=K;++i) rk[adic[i]]=i;
for(int i=1,c=0;i<=K;++i)
if(i==1||adic[i]>adic[i-1]+1){
bli[i]=++c;
bl[c]=br[c]=i;
}else{
bli[i]=c;
br[c]=i;
}
for(int i=K,l=N+1,r=0,lal=N+1,lar=0,wl=0,wr=0;i;--i){
cmin(l,rk[a[i]]);
cmax(r,rk[a[i]]);
if(r-l==K-i){
if(l<lal) wl=0;
else if(bli[r]!=bli[lar]) wl=(lar==br[bli[r]-1]);
if(r>lar) wr=0;
else if(bli[l]!=bli[lal]) wr=(lal==bl[bli[l]+1]);
++wl;
++wr;
if(wl>vl[l]){
vl[l]=wl;
vpl[l]=i;
}
if(wr>vr[r]){
vr[r]=wr;
vpr[r]=i;
}
lal=l;
lar=r;
}
}
int ac=K;
for(int i=K,l=N+1,r=0,lal=N+1,lar=0;i;--i){
cmin(l,rk[a[i]]);
cmax(r,rk[a[i]]);
if(r-l==K-i){
if(lal!=N+1){
for(int j=lal-1;j>=l+1;--j)
for(int k=adic[j]-1;k>adic[j-1];--k)
a[++ac]=k;
for(int j=lar+1;j<=r-1;++j)
for(int k=adic[j]+1;k<adic[j+1];++k)
a[++ac]=k;
}
lal=l;
lar=r;
const int wl=vpl[l]==i?vl[l]:0,wr=vpr[r]==i?vr[r]:0;
if(wl>wr){
if(wl) for(int k=adic[l]-1;k>adic[l-1];--k) a[++ac]=k;
if(wr) for(int k=adic[r]+1;k<adic[r+1];++k) a[++ac]=k;
}else{
if(wr) for(int k=adic[r]+1;k<adic[r+1];++k) a[++ac]=k;
if(wl) for(int k=adic[l]-1;k>adic[l-1];--k) a[++ac]=k;
}
}
}
ll ans=0;
seg::build(1,1,N);
*stmx=*stmn=0;
for(int i=1;i<=N;++i){
while(*stmx&&a[stmx[*stmx]]<a[i]){
seg::add(1,1,N,*stmx==1?1:stmx[*stmx-1]+1,stmx[*stmx],-a[stmx[*stmx]]);
--*stmx;
}
while(*stmn&&a[stmn[*stmn]]>a[i]){
seg::add(1,1,N,*stmn==1?1:stmn[*stmn-1]+1,stmn[*stmn],a[stmn[*stmn]]);
--*stmn;
}
seg::add(1,1,N,stmx[*stmx]+1,i,a[i]);
seg::add(1,1,N,stmn[*stmn]+1,i,-a[i]);
seg::add(1,1,N,1,i,-1);
ans+=seg::tr[1].mnc;
stmx[++*stmx]=stmn[++*stmn]=i;
}
printf("%lld\n",ans);
for(int i=1;i<=N;++i) printf("%d ",a[i]);
puts("");
}
}
int main(){
xm::_();
return 0;
}
