数学公式速记

一、 反演与容斥

a) 综述：

1. 定义：反演就是序列函数的互反关系，即转移矩阵互逆。
2. 作用：将“恰好”之类的严格，放宽成更简洁的条件，方便统计。
3. 另一种理解：求出一个不是那么正确的答案，用反演来修正式子。
4. 分类：二项式反演、斯特林反演、莫比乌斯反演、欧拉反演、Min-max 反演、集合反演等等，下面分别介绍。

b) 二项式反演：

1. 形式：

$$f(k)=\sum_{i\in[0,k]}\binom kig(i)\Rightarrow g(k)=\sum_{i\in[0,k]}(-1)^{k-i}\binom kif(i)$$

$$f(k)=\sum_{i\in[k,+\infty)}\binom ikg(i)\Rightarrow g(k)=\sum_{i\in[k,+\infty)}(-1)^{i-k}\binom ikf(i)$$

2. 使用：题目中若是出现“恰好”k 个满足条件，就可以反演成“指定”k 个满足条件，方便计数；但是实际中可能会出现没想到反演的情况。
3. 利用（差）卷积加速二项式反演：将式子化成如下形式，就可以是 O(nlogn)。

$$\frac{g_k}{k!}=\sum_{i=0}^k\frac{(-1)^{k-i}}{(k-i)!}\cdot\frac{f_i}{i!}$$

$$g_kk!=\sum_{i=k}\frac{(-1)^{i-k}}{(i-k)!}\cdot f_ii!$$

c)斯特林反演：

$$f(k)=\sum_{i\in[0,k]}{k\brace i}g(i)\Rightarrow g(k)=\sum_{i\in[0,k]}(-1)^{k-i}{k\brack i}f(i)$$

同理，可以目瞪出它的剩下三种形式；使用上比较有技巧（指我不会）。

d)数论反演：

1. 莫比乌斯反演：

$$f_k=\sum_{i\mid k}g_i\Rightarrow g_k=\sum_{i\mid k}\mu(i)f_i$$

$$f_k=\sum_{k\mid i}g_i\Rightarrow g_k=\sum_{k\mid i}\mu(i)f_i$$

可以用来解决背包计数的逆问题，并且可以 nlnn 计算。

2. 欧拉反演：

$$\text{Id}=1*\varphi$$

可以用于解决带有 gcd(x,y) 的一类计数问题，例如 2020D2T3。

e)Min-max 容斥：

$$\max\{S\}=\sum_{T\subseteq S}(−1)^{|T|-1}\min\{T\}$$

另有拓展 Min-max 容斥：

$$\text{kmax}\{S\}=\sum_{T\subseteq S}(−1)^{|T|-k}\binom{|T|-1}{k-1}\text{kmin}\{T\}$$

喜闻乐见，它对于期望也成立；对于求 n 个东西期望什么时候全部完工之类问题的时候就可以使用；数据范围也不一定特别小，因为有一些小 trick。

f)集合反演：

$$f(T)=\sum_{S\subseteq T}g(S)\Rightarrow g(T)=\sum_{S\subseteq T}(-1)^{|T|-|S|}f(S)$$

从而可以得到一个重要式子：

$$f(T)=\sum_{S\subseteq T}\sum_{E\subseteq S}(-1)^{|S|-|E|}f(E)$$

可以用来带“交集”形式的式子，详情请见《数树》。

g)单位根反演

$$[n\mid k]=\frac1n\sum_{i\in[0,n-1]}\omega_n^{ik}$$

$$\sum_{i\in[0,m]}[n\mid i][x^i]f(x)=\frac1n\sum_{i\in[0,n-1]}f(\omega_n^i)$$

二、 经典数列：

a)组合数：

1. 定义：$\binom nm=\frac{n!}{m!(n-m)!}$
2. 递推式：$\binom nm=\binom{n-1}m+\binom{n-1}{m-1}$，$(n+1)\binom nm=(m+1)\binom{n+1}{m+1}$
3. 求和式中提取公因式常用的式子：$\binom nm\binom mr=\binom nr\binom{n-r}{m-r}$
4. 生成函数形式（用于解决相当多的组合数求和/卷积）：$\binom nm=\left[x^m\right](1+x)^n$
   例如在 2017 的《组合数问题》中就可以用这种方法快速解决问题。
5. Lucas 定理：$\binom nm\bmod p=\binom{\left\lfloor n/p\right\rfloor}{\left\lfloor m/p\right\rfloor}\binom{n\bmod p}{m\bmod p}\bmod p$
6. Kummer 定理：$v_p\left(\binom nm\right)=\frac{S_p(m)+S_p(n-m)-S_p(n)}{p-1}$。前置：$v_p(n!)=\frac{n-S_p(n)}{p-1}$。其中 Sp(n) 表示 n 在 p 进制下的各位数字和，vp(n) 表示 n 中 p 的幂次。
7. 范德蒙德卷积 $\sum_{k\ge0}\binom{n}{a+k}\binom{m}{b-k}=\binom{n+m}{a+b}$，$\sum_{k\ge0}\binom{m+k}{a}\binom{n-k}{b}=\binom{n+m+1}{a+b+1}$。
8. 上指标反转 $\binom{-n}r=\binom{n+r-1}{r}(-1)^r$

b)第一类斯特林数：

1. 定义：n 个互不相同元素分成 m 个互不区分环排列的方案数，记作 ${n\brack m}$
2. 递推式：${n\brack m}={n-1\brack m-1}+(n-1){n-1\brack m}$
3. 重要式子：

$$\sum_{i\in[1,n]}{n\brack i}=n!$$

$$x^{\overline n}=\sum_{i\in[0,n]}{n\brack i}x^i$$

$$x^{\underline n}=\sum_{i\in[0,n]}(-1)^{n-i}{n\brack i}x^i$$

c)第二类斯特林数：

1. 定义：n 个互不相同元素分成 m 个互不区分集合的方案数，记作 ${n\brace m}$
2. 递推式：${n\brace m}={n-1\brace m-1}+m{n-1\brace m}$
3. 重要式子：

$$x^n=\sum_{i\in[0,n]}{n\brace i}x^{\underline i}$$

下降幂可以换成组合数乘阶乘。

$$\sum_{i\in[0,n]}i^k=\sum_{j\in[0,\infty)}{k\brace j}\binom{n+1}{j+1}j!$$

f) 斐波那契数：

1. 定义：$F_n=F_{n-1}+F_{n-2}$，$F_n=\frac1{\sqrt5}\left(\left(\frac{1+\sqrt5}2\right)^n-\left(\frac{1-\sqrt5}2\right)^n\right)$
2. 性质：

$$f'_n=f'_0F_n+f'_1F_{n-1}$$

$$F_{n-1}F_{n+1}-F_n^2=(-1)^n$$

$$F_{a+b}=F_aF_{b+1}+F_{a-1}F_b=F_{a+1}F_b+F_aF_{b-1}$$

$$a\mid b \Leftrightarrow F_a\mid F_b,(F_a,F_b)=F_{(a,b)}$$

g) 分拆数

五边形数：1,2,5,7,12,15,22,26...i*(3*i-1)/2,i*(3*i+1)/2

分拆数：p[n]=p[n-1]+p[n-2]-p[n-5]-p[n-7]+p[n-12]+p[n-15]-...+p[n-i*[3i-1]/2]+p[n-i*[3i+1]/2]-...-...+...+...-...-...

三、 数论部分：

a) 线性求逆元：

线性求出集合的逆元。

b) 扩展欧拉定理：

$$a\bmod p=a^{(b\bmod\varphi(p))+\varphi(p)}\bmod p(b\le\varphi(p))$$

c) 快速乘、扩展欧几里得与扩展中国剩余定理的板子

d) 迪利克雷卷积相关：

$$\epsilon = 1*\mu, d=1*1, \sigma= \text{Id}*1, \text{Id}=\varphi * 1$$

e) 线性筛与杜教筛：

1. 线性筛：只要函数满足积性就可以使用线性筛。
2. 杜教筛：设 f 和 g 是积性函数，S 是 f 的前缀和，于是：

$$g(1)S(n)=\sum_{i\in[1,n]}(f*g)(i)-\sum_{i\in[2,n]}g(i)S(\lfloor n/i\rfloor)$$

f) 原根：

1. 阶数：设 $x= \delta_m(a)$ 表示最小的 x 满足 $a^x\bmod m=1$。
2. 原根：满足 $\delta_m(a)=\varphi(m)$ 的所有 a。
3. 原根判定：x 是 m 的原根当且仅当对于任意 $\varphi(m)$ 的非自身且非 1 因数都满足 $x^d\bmod m\neq1$
4. 最小原根大小：g<=n^0.25

g) BSGS：

用于求解 $A^x=B\pmod p$，本质上就是分块。

h) 积性函数结论

$$d(ij)=\sum_{a\mid i}\sum_{b\mid j}[\gcd(a,b)=1]$$

$$\varphi(ij)=\frac{\varphi(i)\varphi(j)\gcd(i,j)}{\varphi(\gcd(i,j))}$$

四、 生成函数：

a) Ordinary Generating Function

1. 定义：$f(z)=\sum f_iz^i$，形容一个无标号组合类。
2. 加法运算：表示合并两个集合。
3. 乘法运算：表示两个无标号集合的笛卡尔积。
4. 常用的组合构造：

SEQ：就是集合中元素的所有选择及排列

$$A=SEQ(B) \Rightarrow A(z)=\sum_{i\ge0} B^i(z)=\frac1{1-B(z)}$$

PSET：就是集合中元素的所有选择组合

$$A=PSET(B) \Rightarrow A(z)=\begin{cases} \prod_{n\ge1} (1+z^n)^{B_n}\\ \text{exp}\left(\sum B_n\sum_{i\ge1}\frac{(-1)^{i-1}}iz^{in}\right)\\ \text{exp}\left(\sum_{i\ge1}\frac{(-1)^{i-1}}iB(z^i)\right) \end{cases}$$

MSET：SEQ 的无序版本。

$$A=MSET(B) \Rightarrow A(z)=\begin{cases} \prod_{n\ge1} (1-z^n)^{-B_n}\\ \text{exp}\left(\sum B_n\sum_{i\ge1}\frac{z^{in}}i\right)\\ \text{exp}\left(\sum_{i\ge1}\frac{B(z^i)}i\right) \end{cases}$$

CYC：SEQ 的环上同构版本。

$$A=CYC(B)\Rightarrow A(z)=\sum _ {n\geq 1}\frac{\varphi(n)}{n}\ln\frac{1}{1-B(z^n)}$$

b) Exponential Generating Function

1. 定义：$f(z)=\sum f_i\frac{z^i}{i!}$，形容一个无标号组合类。
2. 加法运算：表示合并两个集合。
3. 乘法运算：表示有标号类的有序合并。
4. 重要的组合构造：基本同理。例如：1/(1-A) 表示 SEQ 构造，expA 表示有标号无顺序组合等等。
5. 关于泰勒展开：下面是一些常用式子的 EGF 的封闭形式：

$$< 1, p, p^2,p^3,\ldots> = e^{px}$$

$$< 1, 0,1,0,1,\ldots> = \frac{e^x+e^{-x}}2=\sinh x$$

$$< a_i=(i-1)!> = \ln\frac1{1-x}$$

c) 常用方法：

• 组合构造的逆构造（方程解）：
  • 已知 $B$ 和 $B=\operatorname{exp} A$，那么就可以用 $\ln B$ 求出 $A$。
  • 背包的 $PSET$ 和 $MSET$（即 01 背包和完全背包）均可以用 $\ln A$ 和莫比乌斯反演求逆。
  • 列出方程来大力解出生成函数的封闭形式。
• 位移算子：
  • OGF 的平移算子：$Left(A)=\frac{A-A_0}x$，$Right(x)=Ax+C$。
  • OGF 的按位放大算子：$𝑓(𝐴) =\frac{x\mathrm df}{\mathrm dx}+C$
  • EGF 的平移算子：$𝐿𝑒𝑓𝑡(𝐴) =\frac{\mathrm df}{\mathrm dx}$，$Right(x)=\int_0^xf\mathrm dx+C$。
    （这也是为什么会有需要解微分方程的情况，也就出现了多项式 $\tan$ 之类东西的组合意义——微分方程的一个解）。
• 取模的 Trick：
  • 对 $x^k-1$ 取模来实现下面这类求和：
    $$\binom nr+\binom n{k+r}+\binom n{2k+r}+\cdots=[x^r](1+x)^n\bmod x^k-1$$

  • 循环卷积：对于模 $x^k-1$ 意义下的多项式乘法。
• 拉格朗日反演：
  $$G(F(x))=x\Rightarrow F_n=\frac1n[x^{-1}]\frac1{G^n(x)}=\frac1n[x^{n-1}]\left(\frac x{G(x)}\right)^n$$
  $$G(F(x))=x\Rightarrow [x^n]H(F(x))=\frac1n[x^{-1}]H'(x)\frac1{G^n(x)}$$
  可以用来解很多的方程；第二个式子则可以用来求出与解相关的式子的值。
  另类拉反：
  $$G(F(x))=x\Rightarrow [x^n]H(F(x))=[x^{-1}]H(x)\frac{G'(x)}{G^{n+1}(x)}$$

• Equivalence theorem (Kleene–Rabin–Scott)等价定理：
  设 $𝑇$ 为一个确定性有限状态自动机的矩阵表示，$𝑣$ 是终止节点的集合，$𝑢 = (1,0,0,0,0,\dots)$，于是可以得出这个字符串类的 OGF 是：
  $$𝐿(𝑧) = 𝑢(1 − 𝑧𝑇)^{-1}𝑣$$
  本质上和高斯消元非常类似。

五、格路计数

https://www.luogu.com/article/6ovnnikq

以下定义都是基于每次只能往右上或左下走这一条件的。

也就是说：当你处于 (x,y) 时，你只能走到 (x+1,y+1) 或 (x+1,y-1)。

我们认为一条路径与一条直线的相交次数就是有多少个整点既在路径上又在直线上。

一条路径与一条直线的不相交就是相交次数为 0，反过来相交就是相交次数不为 0。

记号 [a,b,c,d] 是从 (a,b) 到 (c,d) 的方案数。

记号 <a,b,c,d,k> 就是从 (a,b) 走到 (c,d) 且与直线 y=k 相交的路径数。

记号 {a,b,c,d,k} 就是从 (a,b) 走到 (c,d) 且与直线 y=k 不相交的路径数。

记号 [a,b,k] 就是从 (0,0) 走到 (a,b) 的所有路径与直线 y=k 相交次数之和。

记号 |a,b,k1,k2| 就是从 (0,0) 走到 (a,b) 且与直线 y=k1 和 y=k2 都不相交的路径数。https://www.luogu.com.cn/problem/P3266

记号 ⟨a,b,k1,k2⟩ 就是从 (0,0) 走到 (a,b) 且与直线 y=k1 相交而与 y=k2 不相交的路径数。

接下来罗列的是以下每一框求出来的结果。

$$[a,b,c,d]=\binom{c-a}{(c-a+d-b)/2}$$

$$<a,b,c,d,k>=[a,b,c,2k-d]$$

$$\{a,b,c,d,k\}=[a,b,c,d]-[a,b,c,2k-d]$$

$$[a,b,k]=\begin{cases} \sum_{i\in[(a+b)/2+1,a+1]}\binom{a+1}i&0\le k\le b\\ \sum_{i\in[(a-b)/2+k+1,a+1]}\binom{a+1}i&\text{otherwise} \end{cases}$$

点击查看证明

首先把答案也用一个符号记录 $[a,b,k]$ 。（这个要跟1.中的 $[a,b,c,d]$ 区分一下）

然后上图。

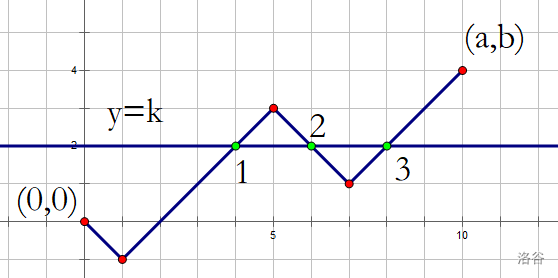
如图要计算绿点的数量。

那么这看起来不是一个简单的组合数能表示的。

所以我们考虑缩小问题规模。

怎么做呢？

先计算最后一个绿点的出现次数。

其实就是路径条数，就是 $res1=[0,0,a,b]$ 。

然后计算不是最后一个的绿点的出现次数。

也就是在这个点 $(i,k)$ 之后再与直线 $y=k$ 有交点。

式子：$\begin{aligned}res2=\sum\limits_{i=0}^{a-1}[0,0,i,k]\times (<i+1,k+1,a,b,k>+<i+1,k-1,a,b,k>)\end{aligned}$

为什么后面是一个奇怪的和呢？

还记不记得 $<a,b,c,d,k>$ 计算的是与 $y=k$ 有交点的路径数?

那么就是说直接 $<i,k,a,b,k>$ 并不是“在这个点之后再与直线 $y=k$ 有交点”的方案数。

所以要先从 $(i,k)$ 走一步再求。

于是就列出了上面那个式子，然后继续化。

$\begin{aligned} res2&=\sum\limits_{i=0}^a[0,0,i,k]\times (<i+1,k+1,a,b,k>+<i+1,k-1,a,b,k>)\\ &=\sum\limits_{i=0}^a[0,0,i,k]\times [i+1,k-1,a,b]\times 2\\ &=\sum\limits_{i=0}^a[0,0,i,k]\times [i,k,a-1,b+1]\times 2 \end{aligned}$

第一步是因为把 2. 中的结论代入，可以发现这个加和的其实是一个东西，直接乘 2 就好了；

第二步就是十分简单的把先从 $(i,k)$ 往前走一步换个方向考虑，改为先从 $(a,b)$ 往回走一步，这样就是上面这个东西了。

接着我们可以发现 $res2=2\times[a-1,b+1,k]$ ！

为什么呢？

让我们看到求 $[a,b,k]$ 第二种想法。

还是上面那图。

我们想，不去缩小规模，可以直接枚举每个绿点会出现在多少条路径中。

式子：$\begin{aligned}[a,b,k]=\sum\limits_{i=0}^a[0,0,i,k]\times[i,k,a,b]\end{aligned}$

意思十分的简单，从 $(0,0)$ 到 $(i,k)$ 再到 $(a,b)$，就是经过 $(i,k)$ 的所有路径了。

然后我们看到 $\begin{aligned}res2=\sum\limits_{i=0}^a[0,0,i,k]\times [i,k,a-1,b+1]\times 2\end{aligned}$

这是不是十分的像？

所以观察一下，我们就可以得到 $res2=2\times[a-1,b+1,k]$

结合 $res1=[0,0,a,b]$，可得 $[a,b,k]=res1+res2=[0,0,a,b]+2\times[a-1,b+1,k]$

这样就可以缩小问题规模了！

为什么呢？

$[a,b,k]=[0,0,a,b]+2\times[a-1,b+1,k]$

看到 $[a-1,b+1,k]$，它可以用上面的式子递归的去分解！

边界？

可以发现当 $a<b$ 时，甚至无法走到 $(a,b)$，所以 $[a,b,k]$ 为零，以这个为边界即可。

然后只要不停分解就好了，可以得到一个十分完美的式子：

$\begin{aligned}[a,b,k]=\sum\limits_{i=1}^a2^{a-i}\dbinom{i}{\frac{a+b}{2}}\end{aligned}$

我们发现居然跟 $k$ 无关！

其实这是因为我们保证了 $y=k$ 处于两个点的纵坐标之间，而当 $y=k$ 不在这两个点的纵坐标之间呢？

我们可以发现一个十分重要的事情，就是 $res1$ 和 $res2$ 不一样了！

具体个怎么不一样呢？

最后一个绿点的出现次数 $res1$ 原本是直接走到 $(a,b)$ 就好了，因为一定会碰到直线 $y=k$ ,但是现在就不一样了。

事实上现在应有 $res1=<0,0,a,b,k>=[0,0,a,2k-b]$ 。

同理的 $res2$ 也会有点不一样，读者自己推一下可以发现 $res2=2\times [a-1,b-1,k]$。

这样 $k$ 就会在式子中，最终会有：

$\begin{aligned}[a,b,k]=\sum\limits_{i=1}^a2^{a-i}\dbinom{i}{\frac{a-b}{2}+k}\end{aligned}$

其实直接考虑把 $(a,b)$ 关于 $y=k$ 对称到 $(a,2k-b)$ 也能得到一样的式子。

上面这条式子还有一个十分重要的优化。

我们抽象一下，就是给你 $n,m$ ，求 $\begin{aligned}\sum\limits_{i=1}^{n}2^{n-i}\dbinom{i}{m}\end{aligned}$

那么我们用组合数恒等式 $\dbinom{n}{m}=\dbinom{n-1}{m-1}+\dbinom{n-1}{m}$ 化。

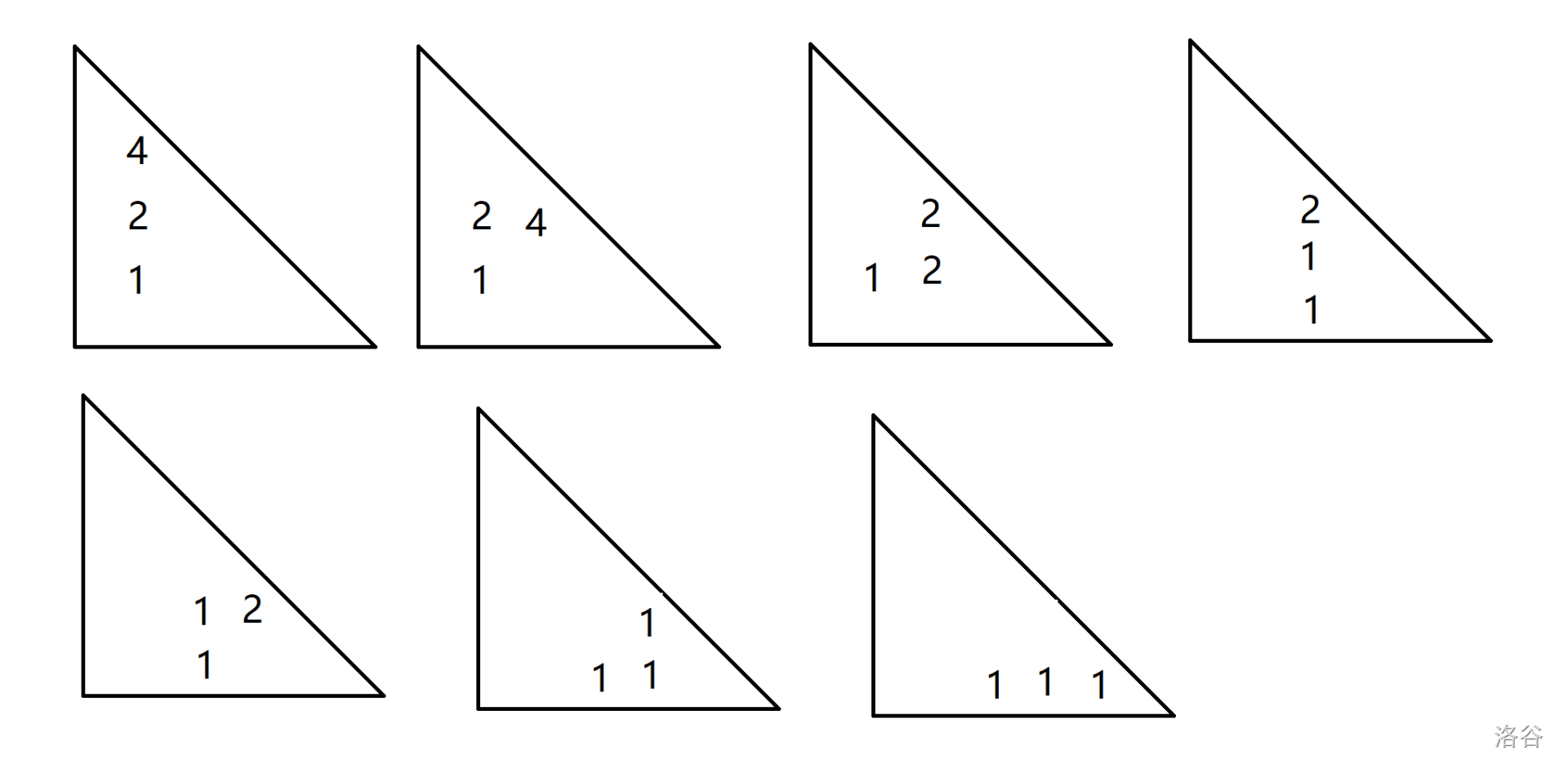
如图，相当于每次都往右下移动，系数除2，然后把最后一项1留下。

最后就是组合数的一行的后缀。

事实上就是 $\begin{aligned}\sum\limits_{i=1}^{n}2^{n-i}\dbinom{i}{m}=\sum\limits_{i=m+1}^{n+1}\dbinom{n+1}{i}\end{aligned}$。

组合数后缀和，这个东西用分块，查询 $q$ 次可以做到 $O(\dfrac{n^2}{B}+qB)$ ，$B$ 为块的大小。

当然，这里有更快的做法。

这样这题到这就结束了。

当 $y=k$ 处于两个点的纵坐标之间的时候答案居然会与 $k$ 无关，这里我们想下这个性质可以怎么去理解。

我们只要证明无论 $k$ 为多少，都与 $k=0$ 的时候的答案是一样的就好了。

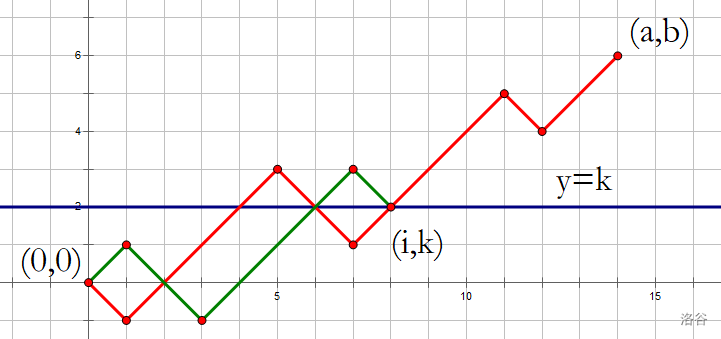
如图，我们假设路径最后与 $y=k$ 的交点在 $(i,k)$ 。

那么我们把从 $(0,0)$ 到 $(i,k)$ 的路径关于中心对称一下（红线变绿线）。

可以发现绿线与 $y=0$ 相交的次数一定等于红线与 $y=k$ 的相交次数，结论便得到了证明。

---

$$|a,b,k_1,k_2|=[0,0,a,b]-<0,0,a,b,k_2>-⟨a,b,k_1,k_2⟩$$

$$⟨a,b,k_1,k_2⟩=|a,2k_1-b,2k_1-k_2,k_2|+⟨a,b,2k_1-k_2,k_2⟩$$

点击查看

考虑把所有不合法的算出来。

把不合法的路线分为碰到 $y=k_2$ 的或不碰到 $y=k_2$ 而碰到 $y=k_3$ 的两种。

我们先把所有一定碰到 $y=k_2$ 的算出来： $res1=<0,0,a,b,k_2>$，

然后让我们关于 $y=k_1$ 对称一下。

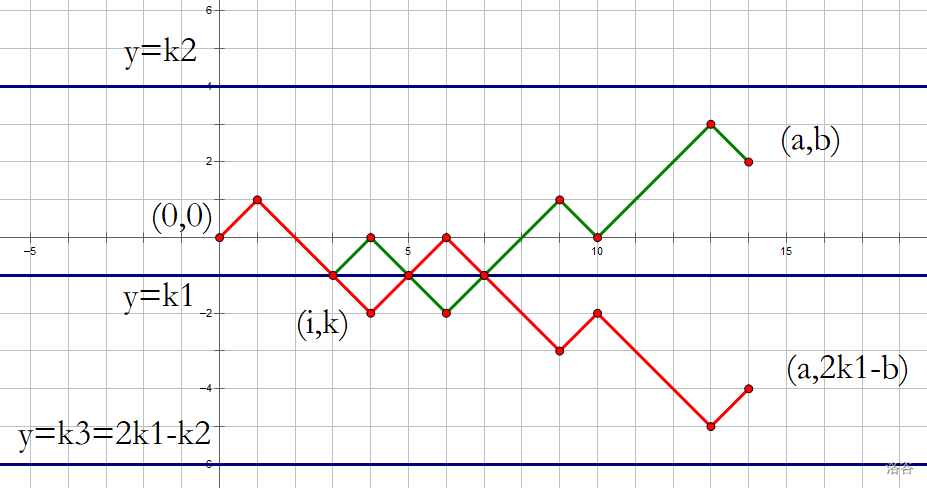
如图，第一个交点是 $(i,k_1)$ ，后面的红线与原来的绿线对称，$y=k_2$ 被对称为 $y=k_3=2k_1-k_2$，$(a,b)$ 被对称为 $(a,2k_1-b)$。

然后我们算经过 $y=k_1$ 而不经 $y=k_2$ 的方案，

可以发现，这要对称前的红线不碰到 $y=k_2$ 和 $y=k_1$ ，对称点之后的红线不碰到 $y=k_3$ 才行。

这没办法算啊，算前半部分的时候还要递归！

然后我就天真的在打表，对称，相交次数中反复横跳，想了好久怎么算，但是都没法做。

但是，当我同 3. 中一样，考虑如何不断缩小问题规模后，终于是找到了一种 $O(n)$ 的偏信息学的办法！

读到此处的读者可以停下来想一想，如何才能像 3. 一样，缩小问题规模呢？说不定你可以找到一种全新的办法。

当然我的想法也十分的有思维难度。

让我们先进行一波定义：

$\left| a,b,k_1,k_2 \right|$ 表示从 $(0,0)$ 走到 $(a,b)$ 且不能碰到 $y=k_1$ 和 $y=k_2$ 的路径数。

$\left\langle\ a,b,k_1,k_2 \right\rangle$ 表示从 $(0,0)$ 走到 $(a,b)$ 且必须碰到 $y=k_1$ 而不能碰到 $y=k_2$ 的路径数。

那么我们现在要求 $\left\langle\ a,b,k_1,k_2 \right\rangle$ 。

而且已经可以得到 $\left| a,b,k_1,k_2 \right|=[0,0,a,b]-<0,0,a,b,k_2>-\left\langle\ a,b,k_1,k_2 \right\rangle$

（就是所有路线中减去不合法的）

然后让我们看到，$\left| a,2k_1-b,k_3,k_2 \right|$ 是个什么东西？

还是上面那图。

$\left| a,2k_1-b,k_3,k_2 \right|$ 就是同时不碰到 $y=k_2$ 也不碰到 $y=k_3$，从 $(0,0)$ 到被对称后的点 $(a,2k_1-b)$ 的路径数。

我们看到这样的路径一定是可以算到我们想求的 $\left\langle\ a,b,k_1,k_2 \right\rangle$ 中的。

但是少算了什么呢？

我们看到要求：“对称前的红线不碰到 $y=k_2$ 和 $y=k_1$ ，对称点之后的红线不碰到 $y=k_3$ 才行”

也就是说对称点之后的红线碰到 $y=k_2$ 是可以的！

而我们直接让这条红线无论如何都不能碰到 $y=k_2$ 了！

所以少算了许多。

那么怎么加回来呢？

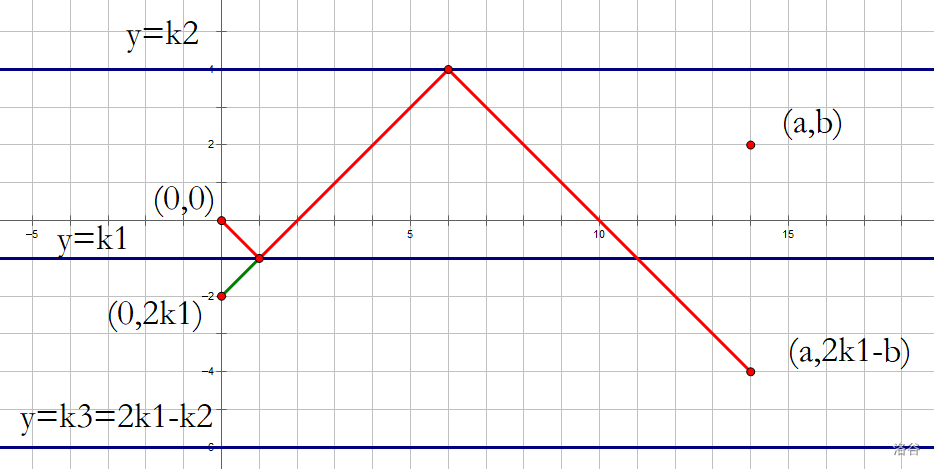
看到这条被我们漏了的红线。

我们想，它一定会先与直线 $y=k_1$ 相交，然后跟 $y=k_2$ 相交。

那么把 $(0,0)$ 也对称下来到 $(0,2k_1)$ 。

一条从 $(0,2k_1)$ 到 $(a,2k_1-b)$ 且不能经过 $y=k_3$ 而必须经过 $y=k_2$ 的路线，是不是就对应着所有被我们漏算的方案呢？

是的！

因为如图所示的绿线，在对称前不会经过 $y=k_3$ ，恰好就代表了对称后它不会经过 $y=k_2$ ；当它与 $y=k_2$ 相交之前，恰好一定会与 $y=k_1$ 有至少一个交点，所有的东西都对上了！

当然了，我们其实与其把 $(0,0)$ 对称下去，还不如把其他东西对称回来，所以就变成了：一条从 $(0,0)$ 到 $(a,b)$ 且不能经过 $y=k_2$ 而必须经过 $y=k_3$ 的路线。

那么我们就得到了一个递归的求解式子！

$\left| a,b,k_1,k_2 \right|=[0,0,a,b]-<0,0,a,b,k_2>-\left\langle\ a,b,k_1,k_2 \right\rangle$

$\left\langle\ a,b,k_1,k_2 \right\rangle =\left| a,2k_1-b,2k_1-k_2,k_2 \right| + \left\langle\ a,b,2k_1-k_2,k_2 \right\rangle$

然后为什么这个把问题规模缩小了呢?

考虑到两条直线间的距离每次都会扩大两倍，而直线太远的时候我们就可以不去考虑直线的影响！

所以如果我们无论怎么走都无法碰到 $y=k_1$ 时就可以直接停止递归。

代码如下：

ll mul[N],inv[N],MOD=998244353;//mul是前缀积，inv是mul的逆元
ll solve1(ll a,ll b,ll k1,ll k2);
ll C(ll x,ll y)//x中选y个 
{
    if(y>x)return 0;
    return mul[x]*inv[y]%MOD*inv[x-y]%MOD;
}
ll walk(ll a,ll b,ll c,ll d)//从(a,b)走到(c,d)
{
    if((c-a+d-b)&1)return 0;
    if(d-b>c-a||b-d>c-a)return 0;
    return C(c-a,(c-a+d-b)/2);
}
ll solve0(ll a,ll b,ll k1,ll k2)//不能碰y=k1和y=k2
{
    if(a<-b||a<b)return 0;
    return (walk(0,0,a,b)-walk(0,0,a,2*k2-b)-solve1(a,b,k1,k2)+MOD+MOD)%MOD;
}
ll solve1(ll a,ll b,ll k1,ll k2)//必须碰y=k1而不能碰y=k2
{
    if(a<-b||a<b)return 0;
    if(a<2*k1-b||a<b-2*k1)return 0;
    return (solve0(a,2*k1-b,2*k1-k2,k2)+solve1(a,b,2*k1-k2,k2))%MOD;
}

预计复杂度 $O(n)$ （因为每次往下递归计算2个，总共递归logn层，同线段树一样，最后会有n次计算），实测这部分会略快于 $O(n)$，因为当直线间的距离越大，计算越快，而距离太小的时候一般可以直接dp，这两个做法速度恰好反着的。当然还是少不了前缀积的预处理 $O(n)$ 的复杂度。

说不定可以用这个代码计算最终答案可以用哪些组合数表示，然后找出一个更优的式子，毕竟所有组合数都在同一行。当然，这就留给有心人去做了。

---

给你一个括号序列 S。你要在左右两头加上总共 n 个括号使整个括号序列合法。求不同的方案数。

如果在左边添加上的括号序列为 A，在右边添加上的括号序列为 B，则当两个方案中的 A 或 B 有一个不同时就视为不同。

将 S 可以配对的括号先配对掉，最后只剩下 a 个 ) 与 b 个 (，如下：))))(((

答案为 $\binom{n+1}{(n+a+b)/2+1}$

六、计算几何

Pick 定理：给定顶点均为整点的简单多边形，皮克定理说明了其面积 ${\displaystyle A}$ 和内部格点数目 ${\displaystyle i}$、边上格点数目 ${\displaystyle b}$ 的关系：${\displaystyle A=i+{\frac {b}{2}}-1}$。

七、图度数序列

兰道定理：竞赛图出度序列从小到大排序，记为 $a$，有 $\forall 1\le k\le N,\sum_{i=1}^ka_i\ge\binom k2$。由于出度越大，缩点成链的位置越浅，故可以说所有取等位置之间构成 SCC。

Erdős–Gallai 定理：一个简单无向图的度数序列 a（降序）合法当且仅当 $\forall 1\le k\le N,\sum_{i=1}^ka_i\le k(k-1)+\sum_{i=k+1}^N\min(k,a_i)$

八、多项式操作

https://www.cnblogs.com/tzcwk/p/dxs-sqr.html

乘法逆

$$B_n=-\frac{1}{A_0}\sum_{i=1}^nA_iB_{n-i}$$

边界 $B_0=\frac{1}{A_0}$。

ln

$$B_n=A_n-\frac1n\sum_{i=1}^{n-1}iB_iA_{n-i}$$

exp

$$B_n=\frac1n\sum_{i=1}^nB_{n-i}A_ii$$