[POJ 3155]Hard Life（最大密度子图）

Description

John is a Chief Executive Officer at a privately owned medium size company. The owner of the company has decided to make his son Scott a manager in the company. John fears that the owner will ultimately give CEO position to Scott if he does well on his new manager position, so he decided to make Scott’s life as hard as possible by carefully selecting the team he is going to manage in the company.

John knows which pairs of his people work poorly in the same team. John introduced a hardness factor of a team — it is a number of pairs of people from this team who work poorly in the same team divided by the total number of people in the team. The larger is the hardness factor, the harder is this team to manage. John wants to find a group of people in the company that are hardest to manage and make it Scott’s team. Please, help him.

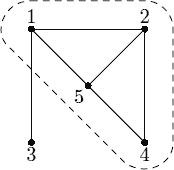
In the example on the picture the hardest team consists of people 1, 2, 4, and 5. Among 4 of them 5 pairs work poorly in the same team, thus hardness factor is equal to ⁵⁄₄. If we add person number 3 to the team then hardness factor decreases to ⁶⁄₅.

Solution

题面丧病…公司的大股东要把自己的儿子放进公司，很可能会取代你的位置，公司里的人与人间有若干条不和的关系，你希望给他分配一个不和关系组数/人数的值最大的垃圾小组

最大密度子图·裸

我用的是naive方法…并没有学论文里的Improved Algorithm

注意最好二分之后check一遍l，用mid很容易出现最后图里一个点也没有的情况

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<queue>
#include<vector>
#include<algorithm>
#include<cmath>
#define INF 1e20
#define eps 1e-6
using namespace std;
int s,t,n,m,head[2005],level[2005],u[1005],v[1005],cnt,ans;
bool vis[1005];
struct Node
{
    int next,to;
    double cap;
}Edges[10005];
void addedge(int u,int v,double c)
{
    Edges[cnt].next=head[u];
    head[u]=cnt;
    Edges[cnt].to=v;
    Edges[cnt++].cap=c;
}
void insert(int u,int v,double c)
{
    addedge(u,v,c);
    addedge(v,u,0);
}
queue<int>q;
bool bfs()
{
    memset(level,-1,sizeof(level));
    q.push(s),level[s]=0;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];~i;i=Edges[i].next)
        {
            int v=Edges[i].to;
            if(level[v]==-1&&Edges[i].cap>eps)
            level[v]=level[u]+1,q.push(v);
        }
    }
    if(level[t]==-1)return false;
    return true;
}
double dfs(int u,double f)
{
    if(u==t||fabs(f)<eps)return f;
    double flow=0,d;
    for(int i=head[u];~i&&flow<f;i=Edges[i].next)
    {
        int v=Edges[i].to;
        if(level[v]==level[u]+1&&Edges[i].cap>eps)
        {    
            d=dfs(v,min(Edges[i].cap,f-flow));
            flow+=d;
            Edges[i].cap-=d;
            Edges[i^1].cap+=d;
        }
    }
    if(flow<eps)level[u]=-1;
    return flow;
}
double dinic()
{
    double res=0,d;
    while(bfs())
    {
        while((d=dfs(s,INF))>eps)res+=d;
    }
    return res;
}
void find()
{
    memset(vis,0,sizeof(vis));
    vis[s]=1,q.push(s);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        if(u>0&&u<=n)++ans;
        for(int i=head[u];~i;i=Edges[i].next)
        {
            int v=Edges[i].to;
            if(!vis[v]&&Edges[i].cap>eps)vis[v]=1,q.push(v);
        }
    }
}
bool check(double mid)
{
    double res;
    memset(head,-1,sizeof(head));
    s=0,t=n+m+1,res=m,cnt=0;
    for(int i=1;i<=n;i++)insert(i,t,mid);
    for(int i=1;i<=m;i++)
    {
        insert(s,i+n,1);
        insert(i+n,u[i],INF),insert(i+n,v[i],INF);
    }
    res-=dinic();
    return res<eps;
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        if(!m){printf("1\n1\n");return 0;}
        for(int i=1;i<=m;i++)scanf("%d%d",&u[i],&v[i]);
        double l=0,r=m,mid;
        while(r-l>1.0/n/n)
        {
            mid=(l+r)/2;
            if(check(mid))r=mid;else l=mid;
        }
        check(l);
        ans=0,find();
        printf("%d\n",ans);
        for(int i=1;i<=n;i++)if(vis[i])printf("%d\n",i);
    }
    return 0;
}