234.LaTeX公式

 需要注意的是:

1.本文只对第四章排版数学公式进行简单整理

2.本文大量内容直接引自官网，尤其是涉及4.开头的标题，为方便读者查阅对比，就不一一删改和引注，你可以点此访问官网对应内容。

3.文中部分LaTeX格式未达到演示效果，可能是由于博客园标准不一样，具体以实验为准

 

 

 

 

TeX

TEX 是高德纳 (Donald E.Knuth) 开发的、以排版文字和数学公式为目的的一个计算机软件 [6]。高德纳从 1977 年开始开发 TEX ，以发掘当时开始用于出版工业的数字印刷设备的潜力。正 在编写著作《计算机程序设计艺术》的高德纳，意图扭转排版质量每况愈下的状况，以免影响他 的出书。我们现在使用的 TEX 排版引擎发布于 1982 年，在 1989 年又稍加改进以更好地支持 8-bit 字符和多语言排版。TEX 以其卓越的稳定性、跨平台、几乎没有 Bug 而著称。TEX 的版本 号不断趋近于 π，当前为 3.141592653。 TEX 读作 “Tech” ，其中 “ch” 的发音类似于 “h” ，与汉字“泰赫”的发音类似。TEX 的拼写 来自希腊词语 τεχνική (technique，技术) 的开头几个字母。在 ASCII 字符环境，TEX 写作 TeX。

LaTeX

L ATEX 为 TEX 基础上的一套格式，令作者能够使用预定义的专业格式以较高质量排版和印 刷他们的作品。L ATEX 的最初开发者为 Leslie Lamport 博士 [1]。L ATEX 使用 TEX 程序作为自己 的排版引擎。当下 L ATEX 主要的维护者为 Frank Mittelbach。 L ATEX 读作 “Lah-tech” 或者 “Lay-tech” ，近似于汉字“拉泰赫”或“雷泰赫”。L ATEX 在 ASCII 字符环境写作 LaTeX。当前的 L ATEX 版本为 L ATEX2ε，意思是超出了第二版，接近但没 达到第三版，在 ASCII 字符环境写作 LaTeX2e。

详见https://www.latex-project.org/

 

在介绍数学公式排版之前，简单介绍一下 AMS 宏集。AMS 宏集合是美国数学学会 (American Mathematical Society) 提供的对 L ATEX 原生的数学公式排版的扩展，其核心是 amsmath 宏 包，对多行公式的排版提供了有力的支持。此外，amsfonts 宏包以及基于它的 amssymb 宏包提 供了丰富的数学符号；amsthm 宏包扩展了 L ATEX 定理证明格式。 本章介绍的许多命令和环境依赖于 amsmath 宏包。这些命令和环境将以蓝色示意。

 

1.插入方式

数学公式有两种排版方式：其一是与文字混排，称为行内公式；其二是单独列为一行排版， 称为行间公式。 

1.1行内公式

行内公式由一对 $ 符号包裹

格式：

其他正文$公式$其他正文

例子：

Add $a$ squared and $b$ squared to get $c$ squared. Or, using a more mathematical approach: $a^2 + b^2 = c^2$

效果：

Add $a$ squared and $b$ squared to get $c$ squared. Or, using a more mathematical approach: $a^2 + b^2 = c^2$

 

1.2行间公式

1.2.1形式一：带编号

单独成行的行间公式在 L ATEX 里由 equation 环境包裹。

equation 环境为公式自动生成一 个编号，这个编号可以用 \label 和 \ref 生成交叉引用，amsmath 的 \eqref 命令甚至为引用 自动加上圆括号；

可以用 \tag 命令手动修改公式的编号，或者用 \notag 命令取消为公式编 号（与之基本等效的命令是\nonumber）。

格式：

其他正文
\begin{equation} 
公式
公式 {暗标记}
公式 \tag{自定义编号}
公式 \notag 

\end{equation} 其他正文

注意：

1.{暗标记}可有可无，主要方便引用，详见例子

2. \notag 为手动取消标号

例子：

Add $a$ squared and $b$ squared 
to get $c$ squared 
\begin{equation} 
a^2 + b^2 = c^2 
\end{equation} 
Einstein says 
\begin{equation} 
E = mc^2 \label{clever} 
\end{equation} 
This is a reference to \eqref{clever}.
It’s wrong to say 
\begin{equation} 
1 + 1 = 3 \tag{dumb} 
\end{equation} 
or 
\begin{equation} 
1 + 1 = 4 \notag 
\end{equation}

效果：

Add $a$ squared and $b$ squared
to get $c$ squared
\begin{equation}
a^2 + b^2 = c^2
\end{equation}
Einstein says
\begin{equation}
E = mc^2 \label{clever}
\end{equation}
This is a reference to \eqref{clever}.
It’s wrong to say
\begin{equation}
1 + 1 = 3 \tag{dumb}
\end{equation}
or
\begin{equation}
1 + 1 = 4 \notag
\end{equation}

 

1.2.2形式二：不带标号

方法一：

 命令 \ [ 和 \ ] 用于生成不 带编号的行间公式

格式：

其他正文
\[公式\]
其他正文

例子：

test effect
 \[ a^2 + b^2 = c^2 \]
test effect

 

效果：

test effect
\[ a^2 + b^2 = c^2 \]
test effect

 

方法二：

方法一与之等效的是 displaymath 环境

格式：

其他正文
\begin{displaymath} 
公式
\end{displaymath}
其他正文

例子：

test effect
\begin{displaymath} 
a^2 + b^2 = c^2 
\end{displaymath}
test effect

效果：

test effect
\begin{displaymath}
a^2 + b^2 = c^2
\end{displaymath}
test effect

 

方法三：

equation* 环境，体现 了带星号和不带星号的环境之间的区别。

格式：

其他正文
\begin{equation*} 
公式
\end{equation*} 
其他正文

例子：

test effect
\begin{equation*} 
a^2 + b^2 = c^2 
\end{equation*} 
test effect

效果：

test effect
\begin{equation*}
a^2 + b^2 = c^2
\end{equation*}
test effect

 

数学模式和文本 

当你使用 $ 开启行内公式输入，或是使用 \[ 命令、equation 环境时，你就进入了所谓的 数学模式。数学模式相比于文本模式有以下特点： 

1. 数学模式中输入的空格全部被忽略。数学符号的间隙默认完全由符号的性质（关系符号、运 算符等）决定。需要人为引入空隙时，使用 \quad 和 \qquad 等命令。详见 4.6 节*。

2. 不允许有空行（分段），公式也无法自动换行或者用 \\ 换行。排版多行公式需要用到 4.4 节*介绍的各种环境。

3. 所有的字母被当作数学公式中的变量处理，字母间距与文本模式不一致，也无法生成单词 之间的空格。如果想在数学公式中输入正体的文本，简单情况下可用 4.7.1 小节*中提供的 \mathrm 命令。或者用 amsmath 提供的 \text 命令2。

*关于文中的4.6节4.4节等指官网文件对应内容并不是指本文的章节，详见文首。

 

 

2.符号

2.1一般符号（单字符）

2.1.1简介

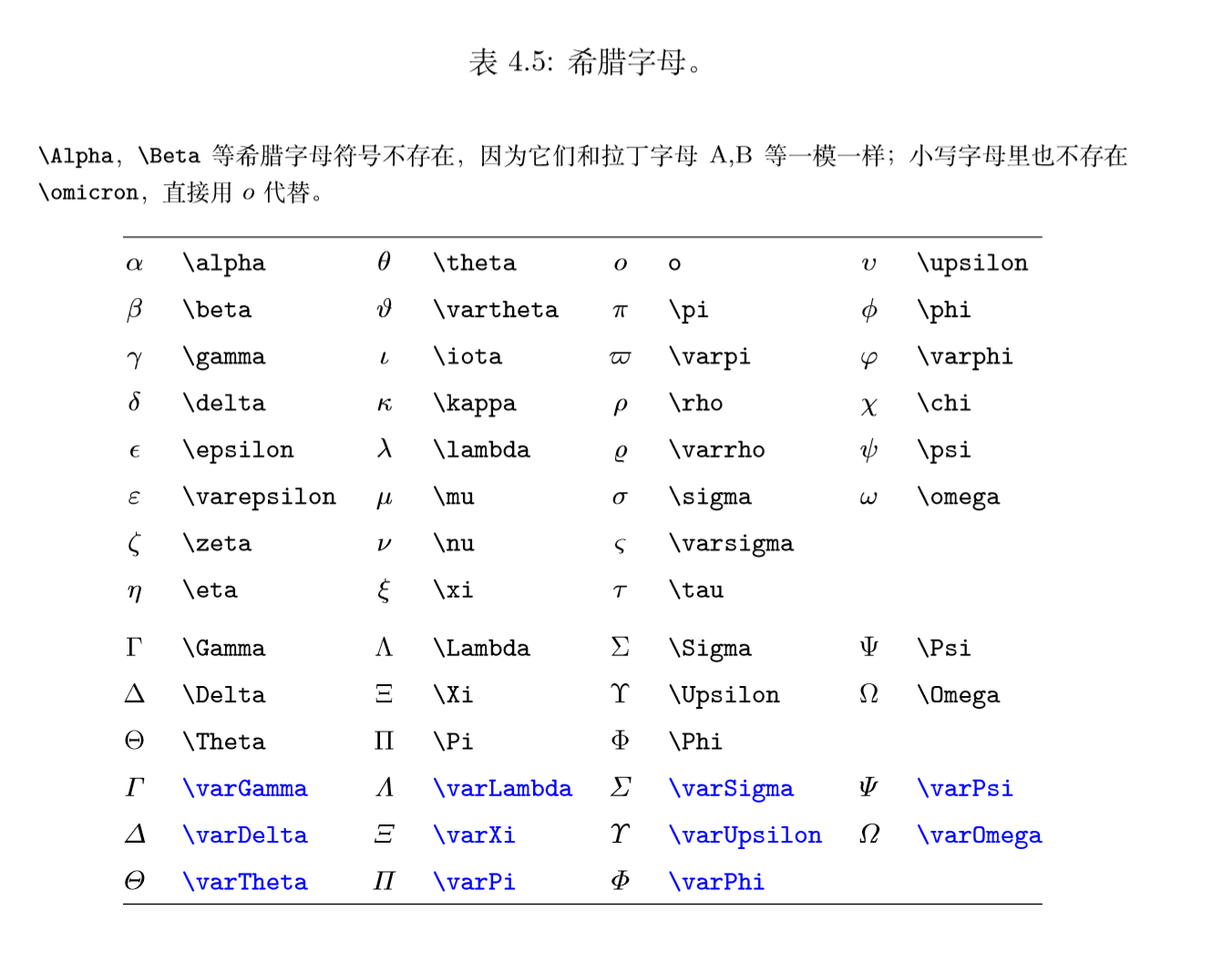
希腊字母符号的名称就是其英文名称，如 α (\alpha)、β (\beta) 等等。

大写的希腊字母为 首字母大写的命令，如 Γ (\Gamma)、∆ (\Delta) 等等。

更多符号命令可参考下表：原文表 4.5 和 4.14 

  

 

2.1.2省略号

省略号 

用命令来生成省略号，相对于直接输入三个点的方式更为合理。

\dots 是 amsmath 命令用来试图帮你在 \ldots 和 \cdots 中自动做决断的 。

\cdots中心省略号  一般用在数学模式的中心线上的符号后面，例如加号 + 或者右箭头 -> 

\ldots低位置省略号 一般用在标点符号的后面，例如句号“ .” or逗号“ ,”

引自Yao_Fairytale

需要注意的是官网文件：\ldots 和 \dots 是完全等效的，它们既能用在公式中，也用来在文本里作为省略号

one, two, three, $\ldots$ one hundred.

one, two, three, $\ldots$ one hundred.

$a_1, a_2, \dots, a_n$ \\ 
$a_1 + a_2 + \cdots + a_n$

$a_1, a_2, \dots, a_n$ \\
$a_1 + a_2 + \cdots + a_n$

 除此之外，在矩阵中可能会用到竖排的 (\vdots) 和斜排的 (\ddots)。

 

 

2.2函数表示符

2.2.1上下标（指数、导数）

用 ^ 和 _ 标明上下标

注意上下标的内容（子公式）一般需要用花括号包裹，否则上下标只对后面的一个符号起作用

导数符号’(′) 是一类特殊的上标，可以适当连用表示多阶导数，也可以在其后连用上标

$p^3_{ij} \qquad 
m_\mathrm{Knuth}\qquad 
\sum_{k=1}^3 k $\\[5pt] 
$a^x+y \neq a^{x+y}\qquad 
e^{x^2} \neq {e^x}^2$
$f(x) = x^2 \quad 
f’(x) = 2x \quad 
f’’^{2}(x) = 4$ 

$p^3_{ij} \qquad
m_\mathrm{Knuth}\qquad
\sum_{k=1}^3 k $\\[5pt]
$a^x+y \neq a^{x+y}\qquad
e^{x^2} \neq {e^x}^2$
$f(x) = x^2 \quad
f’(x) = 2x \quad
f’’^{2}(x) = 4$

 

2.2.2分式

分式使用 \frac{分子}{分母} 来书写。

分式的大小在行间公式中是正常大小，而在行内被 极度压缩。

amsmath 提供了方便的命令 \dfrac 和 \tfrac，令用户能够在行内使用正常大小的 行间公式，或是反过来。

特殊的分式形式，如二项式结构，由 amsmath 宏包的 \binom 命令生成

In display style: 
\[ 3/8 \qquad \frac{3}{8} \qquad \tfrac{3}{8} \]

In display style:
\[ 3/8 \qquad \frac{3}{8} \qquad \tfrac{3}{8} \]

In text style: 
$1\frac{1}{2}$~hours \qquad $1\dfrac{1}{2}$~hours

In text style:
$1\frac{1}{2}$~hours \qquad $1\dfrac{1}{2}$~hours

Pascal’s rule is 
\[ \binom{n}{k} =\binom{n-1}{k} + \binom{n-1}{k-1} \]

Pascal’s rule is
\[ \binom{n}{k} =\binom{n-1}{k} + \binom{n-1}{k-1} \]

 

2.2.3根式

一般的根式使用 \sqrt{...}；表示 n 次方根时写成 \sqrt[n]{...}。

$\sqrt{x} \Leftrightarrow x^{1/2} 
\quad \sqrt[3]{2} 
\quad \sqrt{x^{2} + \sqrt{y}}$

 

$\sqrt{x} \Leftrightarrow x^{1/2}
\quad \sqrt[3]{2}
\quad \sqrt{x^{2} + \sqrt{y}}$

 

 

2.3关系符

2.3.1简介

L ATEX 常见的关系符号除了可以直接输入的 =，>，<，其它符号用命令输入，

常用的有不等号 ̸= (\ne)、大于等于号 ≥ (\ge) 和小于等于号 ≤ (\le)3、约等号 ≈ (\approx)、等价 ≡ (\equiv)、正比 ∝ (\propto)、相似 ∼ (\sim) 等等。

更多符号命令可参考表 4.6 以及表 4.16。 

 

2.3.2自定义

 自定义二元关系符的命令 \stackrel，用于将一个符号叠加在原有的二元关系符之上

\[ 
f_n(x) \stackrel{*}{\approx} 1 
\]

\[
f_n(x) \stackrel{*}{\approx} 1
\]

 

 

2.3算符

2.3.1普通算符

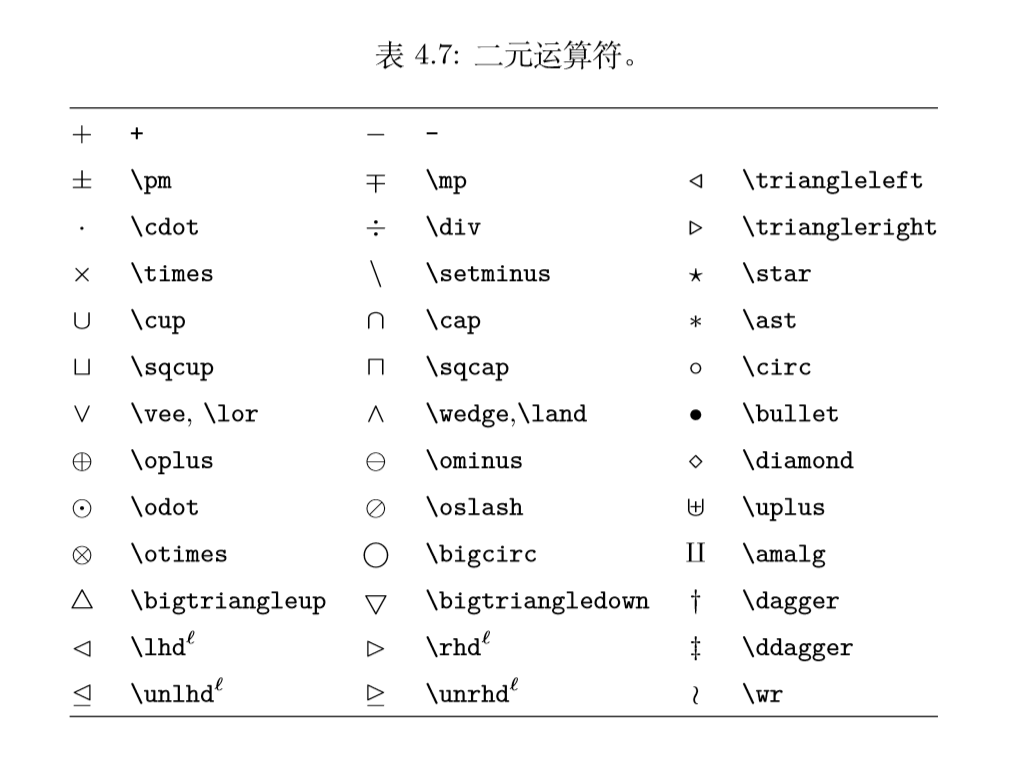
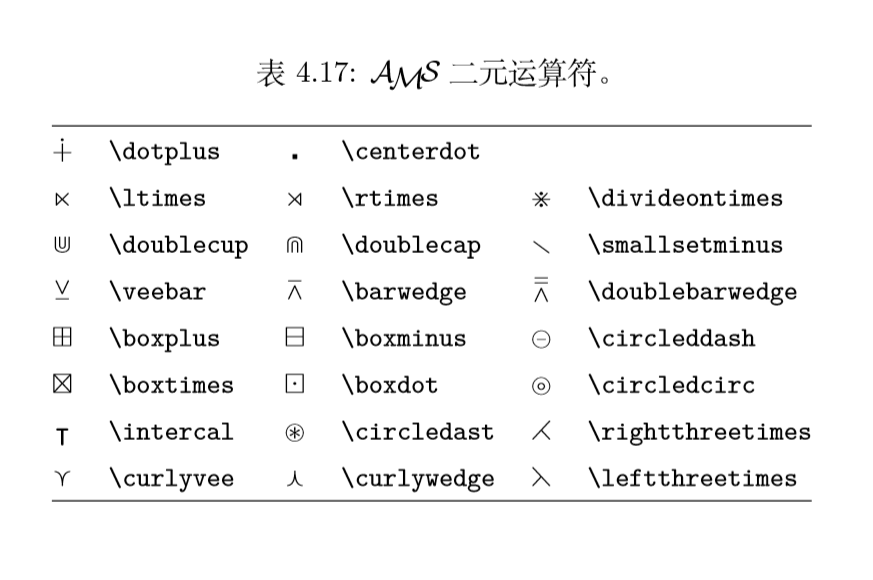
L ATEX 中的算符大多数是二元算符，

除了直接用键盘可以输入的 +、−、∗、/，其它符号用 命令输入，

常用的有乘号 × (\times)、除号 ÷ (\div)、点乘 · (\cdot)、加减号 ± (\pm) / ∓ (\mp) 等等。

更多符号命令可参考表 4.7 以及表 4.17。 

\[
    \lim_{x \rightarrow 0} 
    \frac{\sin x}{x}=1
\]

\[
\lim_{x \rightarrow 0}
\frac{\sin x}{x}=1
\]

 

对于求模表达式，L ATEX 提供了 \pmod 和 \bmod 命令，前者相当于一个二元运算符，后者作为同余表达式的后缀

$a\bmod b \\ 
x\equiv a \pmod{b}$

$a\bmod b \\
x\equiv a \pmod{b}$

 

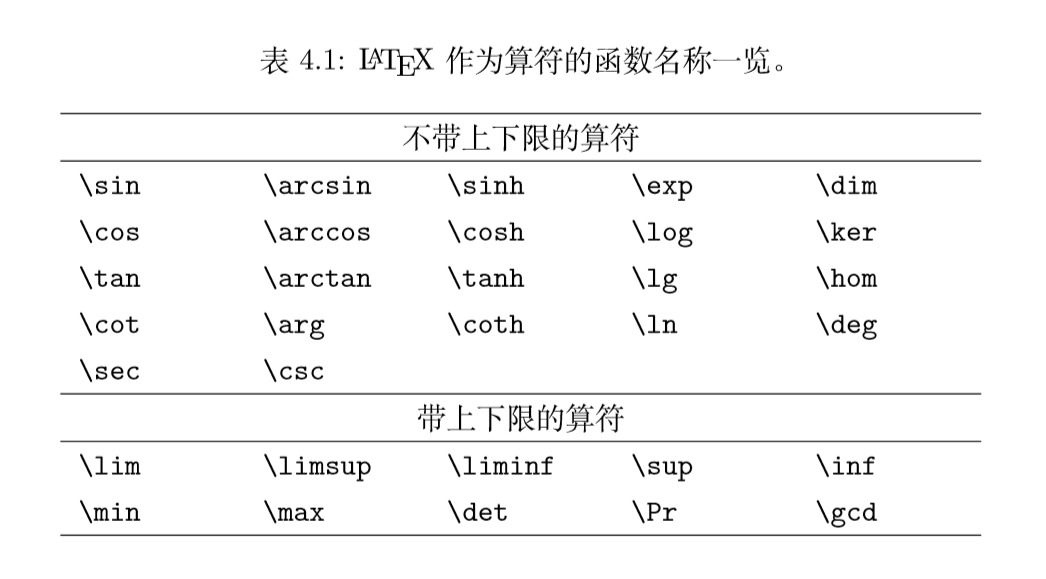
 如果表 4.1 中的算符不够用的话，amsmath 允许用户用 \DeclareMathOperator 定义自己 的算符，其中带星号的命令定义带上下限的算符：

\DeclareMathOperator{\argh}{argh} 
\DeclareMathOperator*{\nut}{Nut}

\[\argh 3 = \nut_{x=1} 4x\]

\DeclareMathOperator{\argh}{argh} 
\DeclareMathOperator*{\nut}{Nut}

\[\argh 3 = \nut_{x=1} 4x\]

 

 

2.3.2巨算符

积分号∫ (\int)、求和号∑(\sum) 等符号称为巨算符。

 

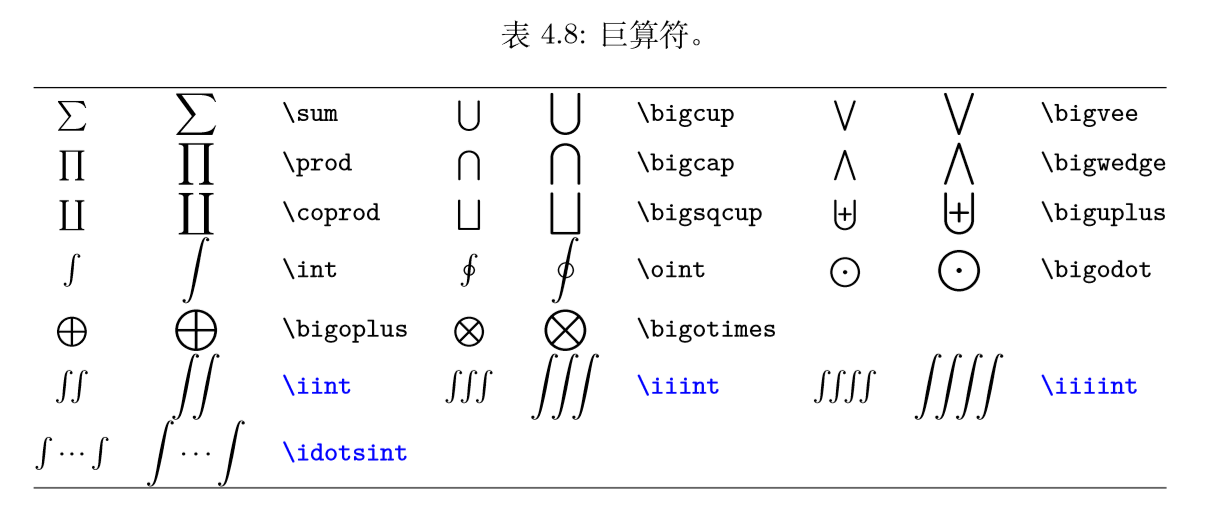
巨算符在行内公式和行间公式的 大小和形状有区别。 

In text: 
$\sum_{i=1}^n \quad 
\int_0^{\frac{\pi}{2}} \quad 
\oint_0^{\frac{\pi}{2}} \quad 
\prod_\epsilon $ \\ 
In display: 
\[\sum_{i=1}^n \quad 
\int_0^{\frac{\pi}{2}} \quad 
\oint_0^{\frac{\pi}{2}} \quad 
\prod_\epsilon \]

In text:
$\sum_{i=1}^n \quad
\int_0^{\frac{\pi}{2}} \quad
\oint_0^{\frac{\pi}{2}} \quad
\prod_\epsilon $ \\
In display:
\[\sum_{i=1}^n \quad
\int_0^{\frac{\pi}{2}} \quad
\oint_0^{\frac{\pi}{2}} \quad
\prod_\epsilon \]

 

 巨算符的上下标用作其上下限。

行间公式中，积分号默认将上下限放在右上角和右下角，求和号默认在上下方；

行内公式一律默认在右上角和右下角。

可以在巨算符后使用 \limits 手动令上下限显示在上下方，\nolimits 则相反。

In text: 
$\sum\limits_{i=1}^n \quad 
\int\limits_0^{\frac{\pi}{2}} \quad 
\prod\limits_\epsilon $ 
In display: 
\[\sum\nolimits_{i=1}^n \quad 
\int\limits_0^{\frac{\pi}{2}} \quad 
\prod\nolimits_\epsilon \]

In text:
$\sum\limits_{i=1}^n \quad
\int\limits_0^{\frac{\pi}{2}} \quad
\prod\limits_\epsilon $ 
In display:
\[\sum\nolimits_{i=1}^n \quad
\int\limits_0^{\frac{\pi}{2}} \quad
\prod\nolimits_\epsilon \]

 

amsmath 宏包还提供了 \substack，能够在下限位置书写多行表达式；subarray 环境更进 一步，令多行表达式可选择居中 (c) 或左对齐 (l)

\[ 
\sum_{\substack{0\le i\le n \\ 
  j\in \mathbb{R}}} 
P(i,j) = Q(n) 
\] 
\[ 
\sum_{\begin{subarray}{l} 
  0\le i\le n \\ 
  j\in \mathbb{R} 
\end{subarray}} 
P(i,j) = Q(n) 
\]

\[
\sum_{\substack{0\le i\le n \\
j\in \mathbb{R}}}
P(i,j) = Q(n)
\]
\[
\sum_{\begin{subarray}{l}
0\le i\le n \\
j\in \mathbb{R}
\end{subarray}}
P(i,j) = Q(n)
\]

 

2.4定界符

2.4.1简介

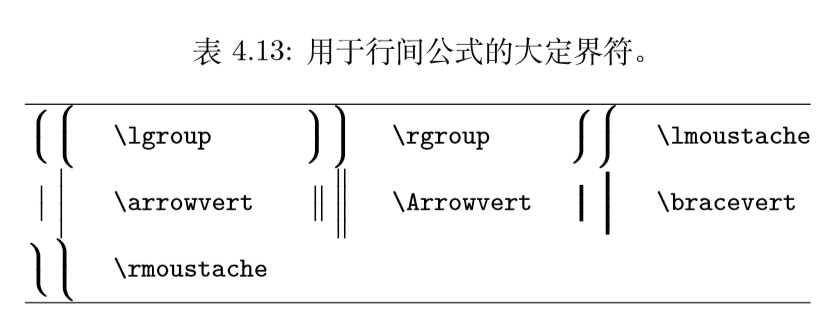
L ATEX 提供了多种括号和定界符表示公式块的边界。除小括号 ( )、中括号 [ ] 之外，其 余都是 L ATEX 命令，包括大括号 \{ \}。表 4.12 和 4.13 给出了更多的括号/定界符命令。 

${a,b,c} \neq \{a,b,c\}$

 

${a,b,c} \neq \{a,b,c\}$

2.4.2自动大小与单双

1、使用 \left 和 \right 命令可令括号（定界符）的大小可变，在行间公式中常用。

      L ATEX 会 自动根据括号内的公式大小决定定界符大小。

      \left 和 \right 必须成对使用。

2、需要使用单个定界符时，另一个定界符写成 \left. 或 \right.  （相当于省略一个，用点代替）

\[1 + \left(\frac{1}{1-x^{2}} 
\right)^3 \qquad 
\left.\frac{\partial f}{\partial t} 
\right|_{t=0}\]

\[1 + \left(\frac{1}{1-x^{2}}
\right)^3 \qquad
\left.\frac{\partial f}{\partial t}
\right|_{t=0}\]

 

2.4.3自定义大小

有时我们不满意于 L ATEX 为我们自动调节的定界符大小。

还可以用 \big、\bigg 等命令生成固定大小的定界符。

更常用的形式是类似 \left 的 \bigl、\biggl 等，以及类似 \right 的 \bigr、\biggr 等

（\bigl 和 \bigr 不必成对出现）。

$\Bigl((x+1)(x-1)\Bigr)^{2}$\\ 
$\bigl( \Bigl( \biggl( \Biggl( \quad 
\bigr\} \Bigr\} \biggr\} \Biggr\} \quad 
\big\| \Big\| \bigg\| \Bigg\| \quad 
\big\Downarrow \Big\Downarrow 
\bigg\Downarrow \Bigg\Downarrow$

 

$\Bigl((x+1)(x-1)\Bigr)^{2}$\\
$\bigl( \Bigl( \biggl( \Biggl( \quad
\bigr\} \Bigr\} \biggr\} \Biggr\} \quad
\big\| \Big\| \bigg\| \Bigg\| \quad
\big\Downarrow \Big\Downarrow
\bigg\Downarrow \Bigg\Downarrow$

使用 \big 和 \bigg 等命令的另外一个好处是：

用 \left 和 \right 分界符包裹的公式块是不允许断行的

（下文提到的 array 或者 aligned 等环境视为一个公式块），

所以也不允许在 多行公式里跨行使用，而 \big 和 \bigg 等命令不受限制。

 

 

3.场景符号

3.1数组

3.1.1简介

为了排版二维数组，L ATEX 提供了 array 环境，用法与 tabular 环境极为类似，

也需要定 义列格式，并用 \\ 换行。

数组可作为一个公式块，在外套用 \left、\right 等定界符

值得注意的是，上一节末尾介绍的 aligned 等环境也可以用定界符包裹。 

\[ \mathbf{X} = \left( 
\begin{array}{cccc} 
x_{11} & x_{12} & \ldots & x_{1n}\\ 
x_{21} & x_{22} & \ldots & x_{2n}\\ 
\vdots & \vdots & \ddots & \vdots\\ 
x_{n1} & x_{n2} & \ldots & x_{nn}\\ 
\end{array} \right) \]

\[ \mathbf{X} = \left(
\begin{array}{cccc}
x_{11} & x_{12} & \ldots & x_{1n}\\
x_{21} & x_{22} & \ldots & x_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
x_{n1} & x_{n2} & \ldots & x_{nn}\\
\end{array} \right) \]

 

3.1.2分段效果

方法一：

利用空的定界符排版

\[ |x| = \left\{ 
\begin{array}{rl} 
-x & \text{if } x < 0,\\ 
0 & \text{if } x = 0,\\ 
x & \text{if } x > 0. 
\end{array} \right. \]

 \[ |x| = \left\{ 

\begin{array}{rl}
-x & \text{if } x < 0,\\
0 & \text{if } x = 0,\\
x & \text{if } x > 0.
\end{array} \right. \]

 

方法二：

用 amsmath 提供的 cases 环境

\[ |x| = 
\begin{cases} 
-x & \text{if } x < 0,\\ 
0 & \text{if } x = 0,\\ 
x & \text{if } x > 0. 
\end{cases} \]

 

\[ |x| =
\begin{cases}
-x & \text{if } x < 0,\\
0 & \text{if } x = 0,\\
x & \text{if } x > 0.
\end{cases} \]

 

3.2矩阵

3.2.1简介

以用 array 环境排版各种矩阵。amsmath 宏包还直接提供了多种排版矩阵的 环境，包括不带定界符的 matrix，以及带各种定界符的矩阵 pmatrix（(）、bmatrix（[）、Bmatrix（ {）、vmatrix（|）、Vmatrix（||）。使用这些环境时，无需给定列格式

\[ 
\begin{matrix} 
1 & 2 \\ 3 & 4 
\end{matrix} \qquad 
\begin{bmatrix} 
x_{11} & x_{12} & \ldots & x_{1n}\\ 
x_{21} & x_{22} & \ldots & x_{2n}\\ 
\vdots & \vdots & \ddots & \vdots\\ 
x_{n1} & x_{n2} & \ldots & x_{nn}\\ 
\end{bmatrix} 
\]

 

\[
\begin{matrix}
1 & 2 \\ 3 & 4
\end{matrix} \qquad
\begin{bmatrix}
x_{11} & x_{12} & \ldots & x_{1n}\\
x_{21} & x_{22} & \ldots & x_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
x_{n1} & x_{n2} & \ldots & x_{nn}\\
\end{bmatrix}
\]

 

3.2.2调节间距

在矩阵中的元素里排版分式时，一来要用到 \dfrac 等命令，二来行与行之间有可能紧贴着， 这时要用到 3.6.6 小节的方法来调节间距

\[ 
\mathbf{H}= 
\begin{bmatrix} 
\dfrac{\partial^2 f}{\partial x^2} & 
\dfrac{\partial^2 f} 
        {\partial x \partial y} \\[8pt] 
\dfrac{\partial^2 f} 
        {\partial x \partial y} & 
\dfrac{\partial^2 f}{\partial y^2} 
\end{bmatrix} 
\]

 

\[
\mathbf{H}=
\begin{bmatrix}
\dfrac{\partial^2 f}{\partial x^2} &
\dfrac{\partial^2 f}
{\partial x \partial y} \\[8pt]
\dfrac{\partial^2 f}
{\partial x \partial y} &
\dfrac{\partial^2 f}{\partial y^2}
\end{bmatrix}
\]

 

3.3向量（重音）

3.3.1重音简介

数学符号可以像文字一样加重音，比如对时间求导的符号 ˙ r (\dot{r})、¨ r (\ddot{r}) 、表 示向量的箭头 ⃗r (\vec{r}) 、表示欧式空间单位向量的 ˆ e (\hat{\mathbf{e}}) 等，详见表 4.9。

3.3.2重音位置

单个符号

使用时要注意重音符号的作用区域，一般应当对某个符号而不是“符号加下标”使用重音

$\bar{x_0} \quad \bar{x}_0$\\[5pt] 
$\vec{x_0} \quad \vec{x}_0$\\[5pt] 
$\hat{\mathbf{e}_x} \quad 
\hat{\mathbf{e}}_x$

$\bar{x_0} \quad \bar{x}_0$\\[5pt]
$\vec{x_0} \quad \vec{x}_0$\\[5pt]
$\hat{\mathbf{e}_x} \quad
\hat{\mathbf{e}}_x$

 

多个字符

也能为多个字符加重音，包括直接画线的 \overline 和 \underline 命令（可叠加使 用）、宽重音符号 \widehat、表示向量的箭头 \overrightarrow 等。

 

 

$0.\overline{3} = 
\underline{\underline{1/3}}$ \\[5pt] 
$\hat{XY} \qquad \widehat{XY}$\\[5pt] 
$\vec{AB} \qquad 
\overrightarrow{AB}$

$0.\overline{3} =
\underline{\underline{1/3}}$ \\[5pt]
$\hat{XY} \qquad \widehat{XY}$\\[5pt]
$\vec{AB} \qquad
\overrightarrow{AB}$

 

\overbrace 和 \underbrace 命令用来生成上/下括号，各自可带一个上/下标公式

$\underbrace{\overbrace{a+b+c}^6 
\cdot \overbrace{d+e+f}^7} 
_\text{meaning of life} = 42$

 

$\underbrace{\overbrace{a+b+c}^6
\cdot \overbrace{d+e+f}^7}
_\text{meaning of life} = 42$

 

3.4证明

3.4.1箭头

除了作为上下标之外，箭头还用于表示过程。amsmath 的 \xleftarrow 和 \xrightarrow 命令可以为箭头增加上下标

\[ a\xleftarrow{x+y+z} b \] 
\[ c\xrightarrow[x<y]{a*b*c}d \]

\[ a\xleftarrow{x+y+z} b \]
\[ c\xrightarrow[x<y]{a*b*c}d \]

 

4.样式

4.1公式间距

4.1.1简介

前文提到过，绝大部分时候，数学公式中各元素的间距是根据符号类型自动生成的，需要我们手动调整的情况极少。

前面两个生成间距的命令 \quad 和 \qquad。

还可能用到的间距包括 \,、\:、\; 以及负间距 \!，

其中 \quad 、\qquad 和 \, 在文本和数学 环境中可用，

后三个命令只用于数学环境。

文本中的 \␣ 也能使用在数学公式中。

 

 

4.1.2场景

一个常见的用途是修正积分的被积函数 f(x) 和微元 dx 之间的距离。注意微元里的 d 用的 是直立体

\[ 
\int_a^b f(x)\mathrm{d}x 
\qquad 
\int_a^b f(x)\,\mathrm{d}x 
\]

\[
\int_a^b f(x)\mathrm{d}x
\qquad
\int_a^b f(x)\,\mathrm{d}x
\]

 

另一个用途是生成多重积分号。如果我们直接连写两个 \int，之间的间距将会过宽，此时 可以使用负间距 \! 修正之。不过 amsmath 提供了更方便的多重积分号，如二重积分 \iint、三 重积分 \iiint 等

\newcommand\diff{\,\mathrm{d}} 
\begin{gather*} 
\int\int f(x)g(y) 
\diff x \diff y \\ 
\int\!\!\!\int 
f(x)g(y) \diff x \diff y \\ 
\iint f(x)g(y) \diff x \diff y \\ 
\iint\quad \iiint\quad \idotsint 
\end{gather*}

\newcommand\diff{\,\mathrm{d}}
\begin{gather*}
\int\int f(x)g(y)
\diff x \diff y \\
\int\!\!\!\int
f(x)g(y) \diff x \diff y \\
\iint f(x)g(y) \diff x \diff y \\
\iint\quad \iiint\quad \idotsint
\end{gather*}

 

4.2多行公式

4.2.1长公式折行

1.通常来讲应当避免写出超过一行而需要折行的长公式

   如果一定要折行的话，优先在等号之 前折行，其次在加号、减号之前，再次在乘号、除号之前。其它位置应当避免折行

2.amsmath 宏包的 multline 环境提供了书写折行长公式的方便环境。

   它允许用 \\ 折行，将 公式编号放在最后一行。多行公式的首行左对齐，末行右对齐，其余行居中。

3.与表格不同的是，公式的最后一行不写 \\，如果写了，反倒会产生一个多余的空行。

   类似 equation*，multline* 环境排版不带编号的折行长公式。

\begin{multline} 
a + b + c + d + e + f + g + h + i \\ 
= j + k + l + m + n\\ 
= o + p + q + r + s\\ 
= t + u + v + x + z 
\end{multline}

 

\begin{multline}
a + b + c + d + e + f + g + h + i \\
= j + k + l + m + n\\
= o + p + q + r + s\\
= t + u + v + x + z
\end{multline}

 

 

4.2.2多个公式罗列

需要罗列一系列公式，并令其按照等号对齐

目前最常用的是 align 环境，它将公式用 & 隔为两部分并对齐。分隔符通常放在等号左边

\begin{align} 
a & = b + c \\
& = d + e 
\end{align}

 

\begin{align}
a & = b + c \\
& = d + e
\end{align}

 

align 环境会给每行公式都编号。我们仍然可以用 \notag 去掉某行的编号。

在以下的例子， 为了对齐加号，我们将分隔符放在等号右边，这时需要给等号后添加一对括号 {} 以产生正常的间距

\begin{align} 
a ={} & b + c \\ 
={} & d + e + f + g + h + i + j + k + l \notag \\ 
& + m + n + o \\ 
={} & p + q + r + s 
\end{align}

 

\begin{align}
a ={} & b + c \\
={} & d + e + f + g + h + i + j + k + l \notag \\
& + m + n + o \\
={} & p + q + r + s
\end{align}

 

align 还能够对齐多组公式，除等号前的 & 之外，公式之间也用 & 分隔

\begin{align} 
a &=1 & b &=2 & c &=3 \\ 
d &=-1 & e &=-2 & f &=-5 
\end{align}

 

\begin{align}
a &=1 & b &=2 & c &=3 \\
d &=-1 & e &=-2 & f &=-5
\end{align}

 

如果我们不需要按等号对齐，只需罗列数个公式，gather 将是一个很好用的环境

align 和 gather 有对应的不带编号的版本 align* 和 gather*。

\begin{gather} 
a = b + c \\ 
d = e + f + g \\ 
h + i = j + k \notag \\ 
l + m = n 
\end{gather}

 

\begin{gather}
a = b + c \\
d = e + f + g \\
h + i = j + k \notag \\
l + m = n
\end{gather}

 

4.2.3多行公式公用编号

1.另一个常见的需求是将多个公式组在一起公用一个编号，编号位于公式的居中位置。

2.为此， amsmath 宏包提供了诸如 aligned、gathered 等环境，与 equation 环境套用。

以 -ed 结尾的 环境用法与前一节不以 -ed 结尾的环境用法一一对应。

3.split 环境和 aligned 环境用法类似，也用于和 equation 环境套用，

区别是 split 只能 将每行的一个公式分两栏，aligned 允许每行多个公式多栏

下面以 aligned 举例：

\begin{equation} 
\begin{aligned} 
a &= b + c \\ 
d &= e + f + g \\ 
h + i &= j + k \\ 
l + m &= n 
\end{aligned} 
\end{equation}

 

\begin{equation}
\begin{aligned}
a &= b + c \\
d &= e + f + g \\
h + i &= j + k \\
l + m &= n
\end{aligned}
\end{equation}