204.数制(进制)
1.概述
1.1定义
数制(Number System)是用一组固定的数字符号和一套统一的规则来表示数目的方法。若用R个基本符号来表示数目则称为R进制,R称为基数。例如二进制的基数为2,数符有2个;十进制的基数为10,数符有10个。
按进位的原则进行计算称为进位计数制。进位计数制中有两个重要的概念:基数和位权
基数是指用来表示数据的数码的个数,超过(等于)此数后就要向相邻高位进一。同一数码处在数据的不同位置时所代表的数值是不同的,它所代表的实际值等于数字本身的值乘上一个确定的与位置有关的系数,这个系数则称为位权,位权是以基数为底的指数函数。例如,128.7=1×102+2×101+8×100+7×10-1。即“128.7”这个数值中的“1”的权值是102,“7”的权值就是10-1。
以十进制为例
(356)10 = 3 × 102 + 5 × 101 + 6 × 100
基数:10 (356)10 = 3 × 102 + 5 × 101 + 6 × 100
位权:102 101 100 (356)10 = 3 × 102 + 5 × 101 + 6 × 100
(位的)权:0 1 2 (356)10 = 3 × 102 + 5 × 101 + 6 × 100
数码:0、1、2 … 9 (356)10 = 3 × 102 + 5 × 101 + 6 × 100
2.常见
在计算机中常用的进位计数制有二进制、八进制、十进制和十六进制。在日常生活中,通常使用十进制表示方法,而计算机内部采用的是二进制表示法,有时为了简化二进制数据的书写,也采用八进制和十六进制表示法。为了区别不同进制的数据,可在数的右下角标注。一般用B(Binary)或2表示二进制数,O(Octal)或8表示八进制数,H(Hexadecimal)或16表示十六进制数,D(Decimal)或10表示十进制。在本书中我们用字母B、O、H、D表示法,如果省略进制字母,则默认为十进制数。
十进制 D decimal
二进制 B binary
八进制 O octal
十六进制 H hexadecimal
2.1十进制
十进制(Decimal notation):用“0、1、2、3、4、5、6、7、8、9”十个数字表示。逢十进一。
表示方法:(5927)10或5927D
权表示法:(5927)10 = 5*103+9*102+2*101+7*100
2.1.1转化
2.1.1.1 整数N进制转10进制
[位权相加法]
(10101)2=(1×24+0×23+1×22+0×21+1×20)10=(21)10
(10101)8=(1×84+0×83+1×82+0×81+1×80)10=(4161)10
(10101)16=(1×164+0×163+1×162+0×161+1×160)10=(65793)10
(BF3C)16=(11×163+15×162+3×161+12×160)10=(48956)10
2.2二进制数
二进制(Binary notation):用“0”和“1”两个数字表示。逢二进一。
运算规则有:0 + 0 = 0 0 × 0 = 0
0 + 1 = 1 0 × 1 = 0
1 + 0 = 1 1 × 0 = 0
1 + 1 = 10 1 × 1 = 1
表示方法:(11011)2或11011B
权表示法:(11011)2 = 1×24+1×23+0×22+1×21+1×20
2.2.1转化
2.2.1.1 整数N进制转2进制
[除法]
十进制转二进制
(117)10=(111 0101)2

[降幂法]
十进制转二进制
(117)10=(111 0101)2
117 - 26 = 117 - 64 = 53 大于0取1 a6=1 高位
53 - 25 = 53 - 32 = 21 大于0取1 a5=1
21 - 24 = 21 - 16 = 5 大于0取1 a4=1
5 - 23 = 5 - 8 = -3 小于0取0 a3=0
5 - 22 = 5 - 4 = 1 大于0取1 a2=1
1 - 21 = 1 - 2 = -1 小于0取0 a1=0
1 - 20 = 1 - 1 = 0 等于0取1 a0=1 低位
[取一分四法]
十六进制转二进制
(A19C)16 =(1010 0001 1001 1100)2
A 1 9 C
1010 0001 1001 1100
2.2.1.2 小数N进制转2进制
[乘法]
(0.8125)10=(0.1101)2
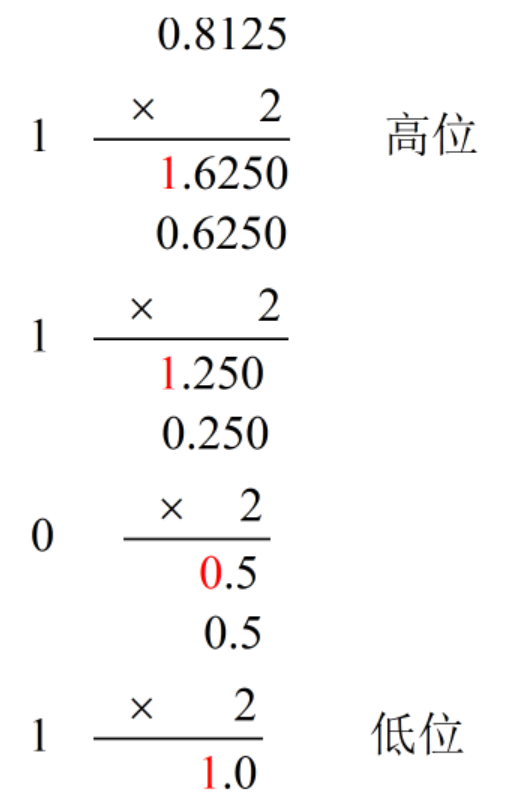
[降幂法]
(0.8125)10=(0.1101)2
0.8125 - 2-1 = 0.8125-0.5 = 0.3125 大于0取1 b1=1 高位
0.3125 - 2-2 = 0.3125-0.25 = 0.0625 大于0取1 b2=1
0.0625 - 2-3 = 0.0625-0.125 <0 小于0取1 b3=0
0.0625 - 2-4 = 0.0625 - 0.0625 = 0 等于0取1 b4=1 低位
2.3八进制
八进制(Octal notation):用“0、1、2、3、4、5、6、7”八个数字表示。逢八进一。
表示方法:(5127)8或5127O
权表示法:(5127)8 = 5×83+1×82+2×81+7×80
2.4十六进制
十六进制(Hexdecimal notation):用“0、1、……9、A、B、C、D、E、F”十六个数字表示。逢十六进一。
表示方法:(5A0D7)16或5A0D7H
权表示法:(5A0D7)16 = 5*164+10*163+0*162+13*161+7*160
2.4.1转化
2.4.1.1整N进制转16进制
[除法]
十进制转十六进制
(48956)10 = (BF3C)16

[取四合一法]
从右向左凑四位
二进制转十六进制
(0011 0101 1011 1111)2 = (35BF)16
0011 0101 1011 1111
3 5 B F
3.转换
位权相加、降幂、乘法、除法、取四(三)合一、取一分四(三)
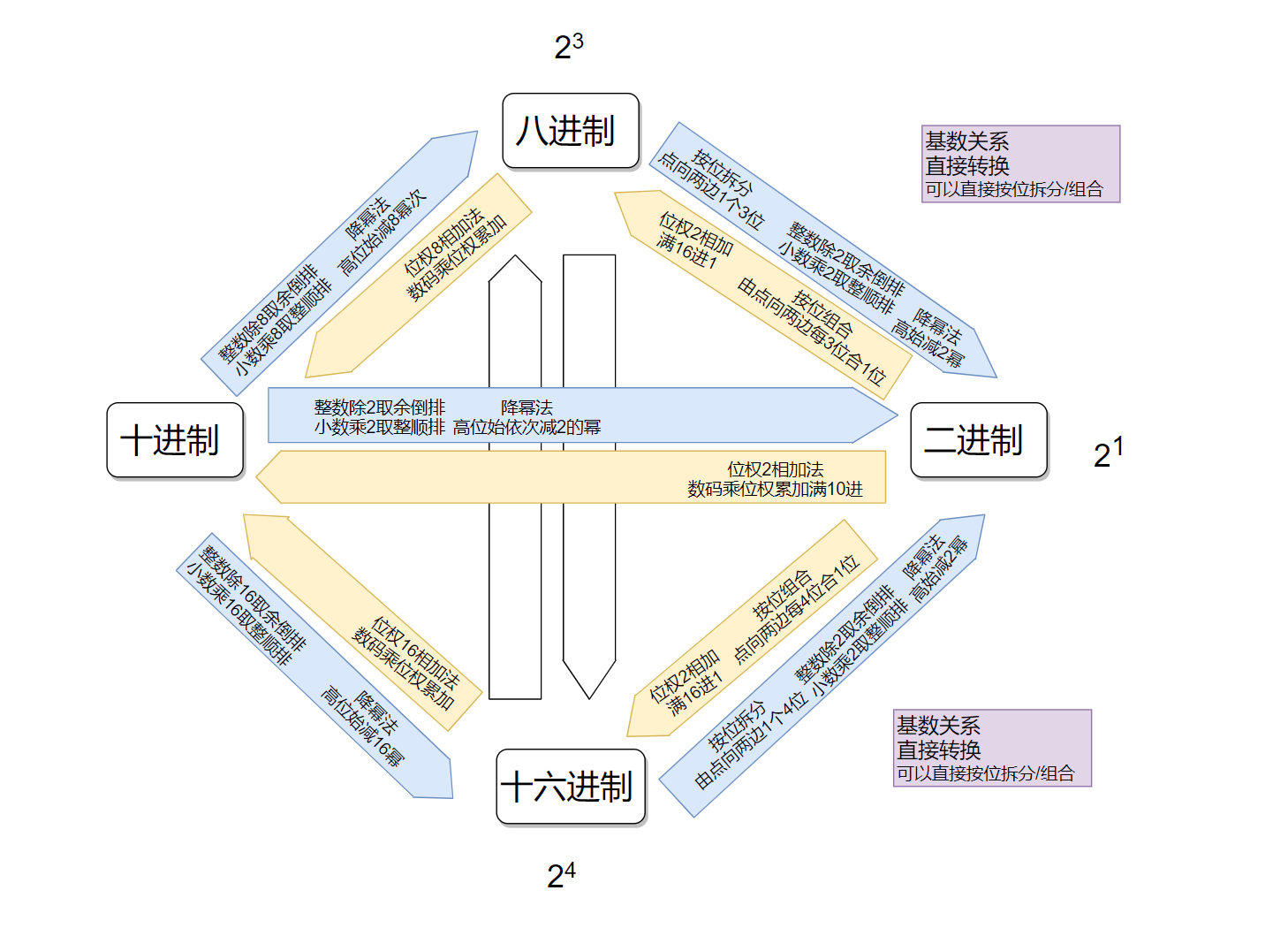
对各种进制数之间的转换,我们要掌握转换的方法和规则,为了便于理解我们将进制的转换分成“二进制数 ↔ 八进制数、十六进制数”、“二进制数 ↔ 十进制数”两大类。
① 二进制、八进制、十六进制之间的转换
● 二进制数转换为八进制、十六进制数
由于81=23(八进制数的一位等于二进制数的三位)、161=24(十六进制数的一位等于二进制数的四位)的关系,它们之间的转换就变得很简单。
其转换规则是以小数点为中心,左右“按位组合”前后不够补0。即八进制是按三位组合,十六进制是按四位组合。
【例1-1】 把(11010111.01111)2转换为八进制数、十六进制数。
(11010111.01111)2=(011,010,111.011,110)2=(327.36)8
(11010111.01111)2=(1101,0111.0111,1000)2=(D7.78)16
● 八进制数、十六进制数转换为二进制数
其转换规则仍是以小数点为中心,“按位展开”(八进制数的一位等于二进制数的三位、十六进制数的一位等于二进制数的四位),最后去掉前后的0。
【例1-2】把(327.36)8、(D7.78)16 转换为二进制数。
(327.36)8=(011,010,111.011,110)2=(11010111.01111)2
(D7.78)16=(1101,0111.0111,1000)2=(11010111.01111)2
② 二进制、八进制、十六进制与十进制之间的转换
● 二进制数、八进制数、十六进制数转换为十进制数
二进制数、八进制数、十六进制数转换为十进制数,其转换规则相同,是“按权展开相加”。同十进制的展开一样,只是其权位不同而已。

● 十进制数转换为二进制数、八进制数、十六进制数
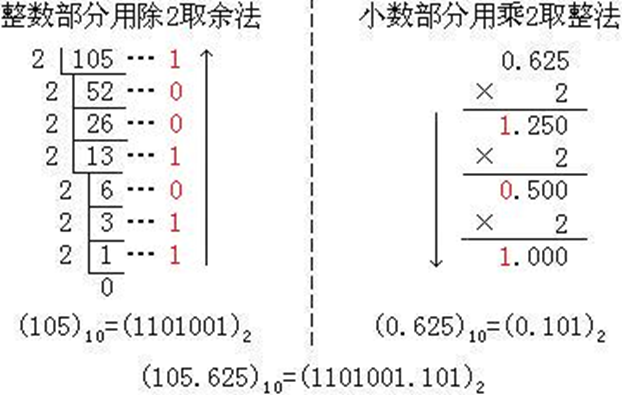
十进制数转换成二进制数分两种情况进行,整数部分和小数部分,具体规则如下所示。
整数部分:除2取余倒排。即采用除2取余,直到商为0,先得的余数排在低位,后得的余数排在高位。
小数部分:乘2取整顺排。即采用乘2取整数,直到值为0或达到精度要求,先得的整数排在高位,后得的整数排在低。
例:将(105.625)10转换成二进制数。
4.注意
4.1表示个数
n位X进制数可表示Xn个数
n位二进制数可以表示2n个数
4.2关于乘法
X进制数 × 基数X = X尾加0
3000H × 16D = 30000H
25 × 10 =250
4.3常用表
| 二进制 | 十进制 | 十六进制 | 八进制 |
| B | D | H | O |
| 0000 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 |
| 0010 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 |
| 0100 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 |
| 0110 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 |
| 1000 | 8 | 8 | 10 |
| 1001 | 9 | 9 | 11 |
| 1010 | 10 | A | 12 |
| 1011 | 11 | B | 13 |
| 1100 | 12 | C | 14 |
| 1101 | 13 | D | 15 |
| 1110 | 14 | E | 16 |
| 1111 | 15 | F | 17 |
| 10000 | 16 | 10 | 20 |
| 20=1 | 21=2 | 22=4 | 23=8 |
| 24=16 | 25=32 | 26=64 | 27=128 |
| 28=256 | 29=512 | 210=1024 | 211=2048 |
| 212=4096 | 213=8192 | 214=16384 | 215=32768 |
| 216=65536 | |||
| 160=1 | 161=16 | 162=256 | 163=4096 |
| 164=65536 | |||




