150.关系

1.关系

1.1关系

事物之间（客体之间）的相互联系，称为关系

n元笛卡尔积A1×A2× …… ×An反映了 n 个客体之间的关系，所以是 n元关系。

序偶〈a，b〉实际上反映了二个元素之间的关系，从而是二元关系。

注意：关系和笛卡尔乘积

笛卡尔乘积的任何子集都可以定义一种二元关系。

设集合X={1, 2, 3, 4}，Y={1, 2}，则X ×Y = {<1,1 >，<1,2 >，< 2,1 >，< 2,2 >，< 3,1 >，< 3,2 >，< 4,1 >，< 4,2 >}

R1 = {<x , y>| x ∈X∧ y ∈Y ∧ x>y } = {<2 , 1>， <3 , 1>， <3 , 2>， <4 , 1>， <4 , 2>， <4 , 3>  }

R2 = {<x , y>| x ∈X∧ y ∈Y ∧ x=y2 } = {<1 , 1>， <4 , 2> }

R2 = {<x , y>| x ∈X∧ y ∈Y ∧ x=y } = {<1 , 1>， <2 , 2> } R1，R2，R3 均为二元关系。

 

1.2序偶

由二个具有给定次序的客体所组成的序列称为序偶，记作〈x，y〉
说明：在序偶中二个元素要有确定的排列次序。
即：若 a ≠ b 时，则〈a，b〉 ≠ 〈b，a〉若〈x，y〉=〈a，b〉 则 （x = a ∧ y = b）
多重序偶：三重序偶〈x，y，z〉=〈〈x，y〉，z〉
　　　　　n重序偶〈x1，…，xn〉=〈〈〈〈x1，x2〉，x3〉…〉，xn〉

 

重要关系

2.二元关系

2.1定义

设 A×B = {〈x，y〉|  (x ∈A) ∧ (y ∈B) }，若集合R ⊆A×B，则称 R 是从 A 到 B的一个二元关系。

即二元关系 R 是以序偶作为元素的集合。若〈x，y〉∈ R，则记作  x R y，否则，记作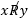

注：A×B 的任何子集都称作从 A 到 B的二元关系，特别当 A = B 时，称作 A上的关系。

 

2.2表示方法

2.2.1枚举法（列举法）

二元关系定义如图：

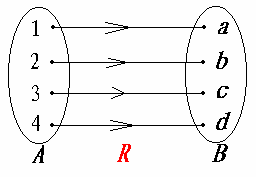
可写成：R = {< 1, a > ，< 2,b > ， < 3, c > ， < 4, d >}
由定义可见：关系是一个集合，∴定义集合的方法都可以用来定义关系。

 

2.2.2谓词公式表示法

前面讲述，集合可用谓词公式来表达，所以关系也可用谓词公式来表达。
例如：实数集合R上的“>” 关系可表达为：“>” = {〈x，y〉| x ∈R ∧ y ∈R ∧ x>y }

 

2.2.3关系矩阵表示法

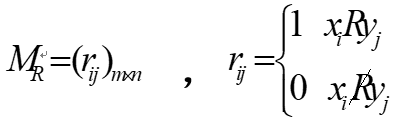
规定：
(a)对于二元关系的序偶 <x , y> ，其左元素表示行，右元素表示列；
(b)若 xi R yj ，则在对应位置上记“1”，否则记“0”。
例如：已知集合 A={1, 2, 3, 4}，并定义A上的关系R={⟨1,2⟩,⟨1,3⟩,⟨2,1⟩,⟨2,2⟩,⟨3,3⟩,⟨4,3⟩}
则R的关系矩阵为

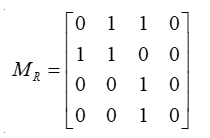
例如：设 X={a，b，c}，Y={1，2}，R1是Ｘ→Ｙ的关系，
称 R1是Ｘ→Ｙ的全域关系，

其关系矩阵为

 

 

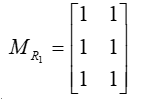
2.2.4关系图表示法

规定：
(a) 把Ｘ，Ｙ集合中的元素以点的形式全部画在平面上；
(b)若 x_i R y_j ，则在 x_i 和 y_j 之间画一条有向弧，反之，不画任何曲线。

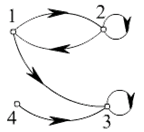
例如：已知集合 A={1, 2, 3, 4}，并定义A上的关系

则R的关系图为

 

 

 

2.3关系的定义域和值域

设R是一个二元关系，令集合 D(R) ={ x | ∃ y (<x, y> ∈R) }；集合 R(R) ={ y | ∃ x (<x, y> ∈R) }；

则称D(R)为R的定义域， R(R)为R的值域。

例如：设X={1, 2, 3, 4, 5, 6}，Y = {a, b, c, d, e, f}，
令R ={<1,a >< 2,b >< 3, c >< 4,d >}，
则R是X到Y的二元关系。
R的定义域：D(R) ={1, 2, 3, 4}，R的值域： R(R) ={a, b, c, d}。

一般情况，称X为R的前域，称Y为R的陪域。

 

2.4特殊二元关系

定义：设 R 是A × A的子集，

①若R =A × A ，则称R是 A上的全域关系，即R = A × A = { <x , y> | x ,y ∈A }.

  全域关系R1 = A×A 

自反的，对称的，可传递的。

 

②若R= Ø，则称R是A上的空关系.

  空关系R2 =Ø

反自反的，对称的，反对称的，可传递的。

 

③集合A上的恒等关系：I _A = { <x , x> | x  ∈A }.

  恒等关系R3 = { < 1 , 1 >   < 2 , 2 >   < 3 , 3 >  } 

自反的，对称的，反对称的，可传递的

 

 

其它常用关系：

  

 

 

2.5关系的五种性质   

自反，反自反，对称，反对称，传递

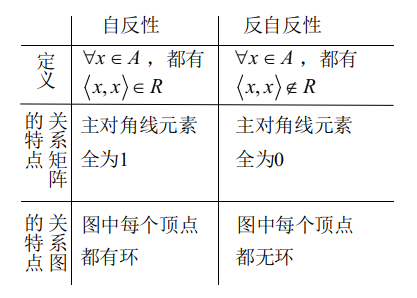
1、自反性

设 R是集合X中的二元关系，若对于每一个 x ∈X ，都有 x R x ，则称R具有自反性。

     注：X上R是自反的  ⇔  ∀x ( x ∈X → x R x ).

例如：设 X = {a , b , c}，R = {< a , a > < b , b > < c , c > < a , b >} 则R是自反的关系。

主对角线元素都为  1；  

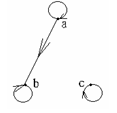
图中每个顶点都有环。

 

2、反自反性

设 R是集合X中的二元关系，若对于每一个 x ∈X ，都有 x x ，则称R具有反自反性。

     注：X上R是自反的  ⇔  ∀x ( x ∈X → x x ).

例如：设 X = {1 , 2 , 3}，R1 = { < 1 , 2 >  < 2 , 1 > };R2 = { < 1 , 2 > } ；R3 = { < 2 , 1 > };

则R1， R2， R3都是反自反的。

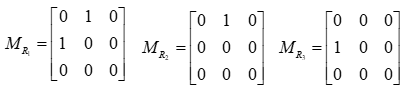
 主对角线元素都为  0；

例如：设 X = {1 , 2 , 3}，R1 = { < 1 , 2 >  < 2 , 1 > };R2 = { < 1 , 2 > } ；R3 = { < 2 , 1 > };

则R1，R2，R3都是反自反的。

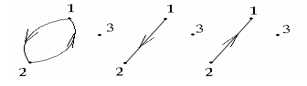
图中每个顶点都无环。

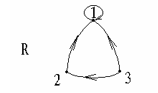
例如：设 X = {1 , 2 , 3}，R4 = { < 1 , 1 >  < 2 , 1>   < 3 , 1>   < 3 , 2 > };

则 R4 既不是自反的，也不是反自反的。

 

 

3、对称性

设 R是集合X中的二元关系，对于任意的 x ，y ∈X ，如果每当有 x R y ，都必有 y R x ，则称R在X上具有对称性。

注：X上R是对称的 ⇔∀x ∀y ( x ∈X ∧y ∈X ∧x R y → y R x ).

例如：设 X = {1 , 2 , 3}，R = {< 1 , 1 > < 2 , 1 >  < 1 , 2 > < 3 , 2 >  < 2 , 3 > } 则R是对称的关系。

对称矩阵  

 

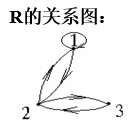
若两顶点间有边，则必有一对方向相反的边

 

4、反对称性

设 R是集合X中的二元关系，对于任意的 x ，y ∈X ，如果每当有 x R y 和 y R x ，都必有 x = y，则称R在X上具有反对称性。

     注：X上R是反对称的  ⇔  ∀x ∀y ( x ∈X ∧y ∈X ∧x R y ∧y R x → x = y ).

分析：① 若前件 x R y ∧y R x 为“T”，且后件 x = y 也为“T”，则 R是反对称的；

②若前件 x R y ∧y R x 为“F”（有三种情况），后件不论是真还是假，命题均为“T”，则 R是反对称的。

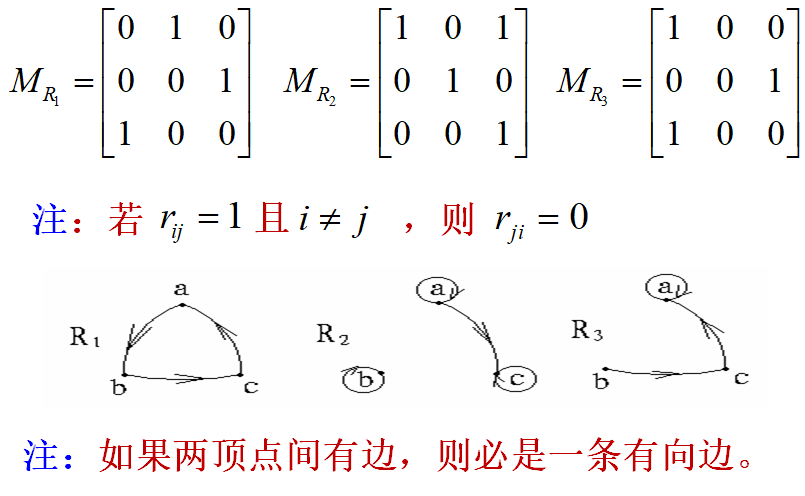
例1：设 X = {a , b , c}，R1 = { < a , b >  < b , c >  < c , a >  }，R2 = {< a , c > < a , a > < b , b > < c , c > } ，

R3 = {< a , a > < b , c > < c , a >  } ，则R1， R2， R3 均是反对称的。

 

 

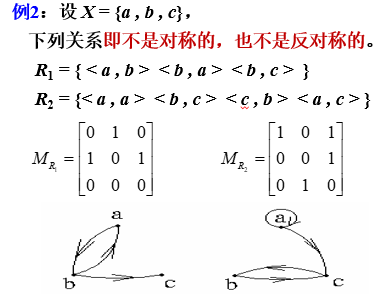
5、传递性

设 R是集合X中的二元关系，对于任意的 x ，y ，z ∈X ，如果每当有 x R y ∧ y R z ，就必有 x R z 。

则称R在X上具有传递性

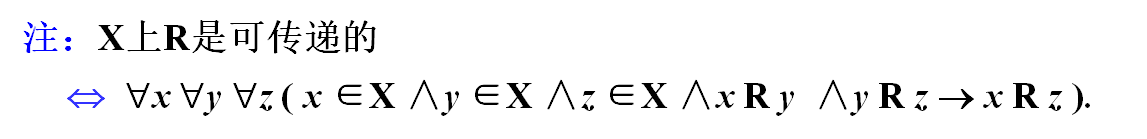
分析：① 若前件 x R y ∧y R z 为“T”，且后件 x R z 也为“T”，则 R是可传递的；

②若前件为“F”（有三种情况），后件不论是真还是假，命题均为“T”，则 R是可传递的。

例1：设 X = {a , b , c}，则下列关系均是可传递的。

         R1 = { < a , a >  < a , b >  < a , c >  < b , c > }

         R2 = {< a , b >}

         R3 = {< a , b >   < a , c >  }

         R4 = Ø

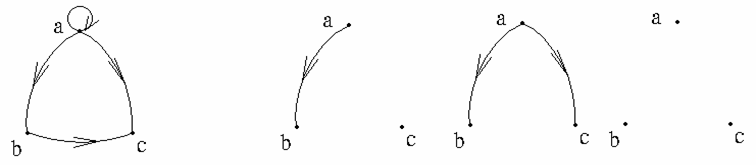
下列关系是不可传递的：
R5 = { < a , a > < a , c > < c , a > }
R6 = { < a , b > < b , c > < c , a > }

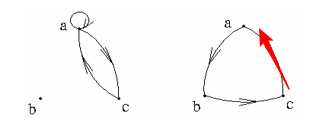
R关系图：遍历每一个结点，其结点出径和入径的结点也可连通直接相连，若只有出或入则满足

关系矩阵：

复合矩阵法

思路：设M是R的关系矩阵，若M*M为M的子集，则R具有传递性。

判断方法：计算M*M，M*M为M的子集的意思是，在方阵对应的同行同列的位置，

若对于M，该数为0，则对于M*M，该数必为零，否则R不具有传递性。

即：若M中的a[i][j] == 0, 则必有M*M中的c[i][j] == 0

#include <iostream>
using namespace std;
const int maxn = 100;
int a[maxn][maxn], c[maxn][maxn];
 
int main()
{
    int i, j, k, flag = 0;
    int n;
    cout << "请输入二元关系对应方阵（n * n）的行数：\n";
    cin >> n;
    cout << "请输入此方阵：\n";
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
            cin >> a[i][j];
    }
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            for (k = 0; k < n; k++)
            {
                c[i][j] = c[i][j] + a[i][k] * a[k][j];
            }
        }
    }
    cout << endl;
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            cout << c[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            if (a[i][j] == 0)
            {
                if (c[i][j] != 0)
                {
                    cout << "No transitivity！\n";
                    return 0;
                } 
            }
        }
    }
    cout << "Transitivity!\n";
    return 0;
}
 

 

利用矩阵表示方法，遍历这个矩阵如果遇到一个等于1的位置，记录位置，利用其纵坐标当下一个数的横坐标，在此横坐标下找到是1的位置，记录这个位置，在利用上一个数位置的横坐标和这个数的纵坐标找到一个新的位置，如果这个位置上是1，那么这个数就具有可传递性，然后继续遍历进行这个循环操作，知道检查到所有的数都对上了，这个二元关系才可说具有可传递性，有一个不符的都不是可传递性的二元关系。

#include <iostream>  
using namespace std;  
const int MAXN = 100;  
int A[MAXN][MAXN];  
int main()  
{  
    cout<<"请输入具有二元关系的两个集合的大小：\n";  
    int x , y ;  
    cin>>x>>y;  
    cout<<"请输入这两个集合的二元关系矩阵表示法：\n";  
    for(int i = 0 ; i < x ; i++)  
        for(int j = 0 ; j < y ; j++)  
            cin>>A[i][j];  
    int p = 0 ;  
    for(int i = 0 ; i < x ; i++)  
    {  
        for(int j = 0 ; j < y ; j++)  
        {  
            if( 1 == A[i][j] )  
            {  
                for(int k = 0 ; k < y ; k++)  
                {  
                    if( 1 == A[j][k] && 1 != A[i][k] )  
                    {  
                        p = 1;  
                        break;  
                    }  
                }  
            }  
        }  
    }  
    if(p)  
        cout<<"这个二元关系不具备可传递性！";  
    else  
        cout<<"这个二元关系具备可传递性！";  
}  

 

 

 

注：若 X = Φ ，则X上的空关系 Φ具有反自反的，对称的，反对称的，可传递的。

 

2.6关系的合成

 

2.6.1关系的复合

（1）定义：

设 R是X→Y的二元关系，S是Y→Z的二元关系，于是可得X →Z的二元关系：
{ <x , z> | x∈X∧z∈Z∧∃ y (y∈Y∧x R y∧y S z ) }  

称此集合为R与S的复合关系，记为R◦S 或 RS.

例如：设 X = {1 , 2 , 3 , 4 , 5 }，
R，S均为X→X的关系，且
R = { <1,2> <3,4> <2,2> }
S = { <4,2> <2,5> <3,1> <1,3> }
则
R◦S = { <1,5> <3,2> <2,5> }
S◦R = { <4,2> <3,2> <1,4> }

R◦S  ≠  S◦R ，复合关系“◦”不满足交换律.

讨论：

⑴ R ◦ S为新的二元关系；

⑵ R ◦ S ⊆ X×Z

⑶ 当 <x , y>∈R与 <y , z>∈S，才有<x , z>∈ R ◦ S .

注：R1R2有定义，但R2R1不一定有定义，即使有定义，也不一定有R1R2＝ R2R1。

 

 

 

 

（2）复合关系的矩阵表示

逻辑加法： 0+0=0 0+1=1 1+0=1 1+1=1

布尔矩阵的布尔乘法：把矩阵乘法中的“+”改为∨，“+”改为∧，其它不变。记为 M_R◦M_S 。

 

 

 

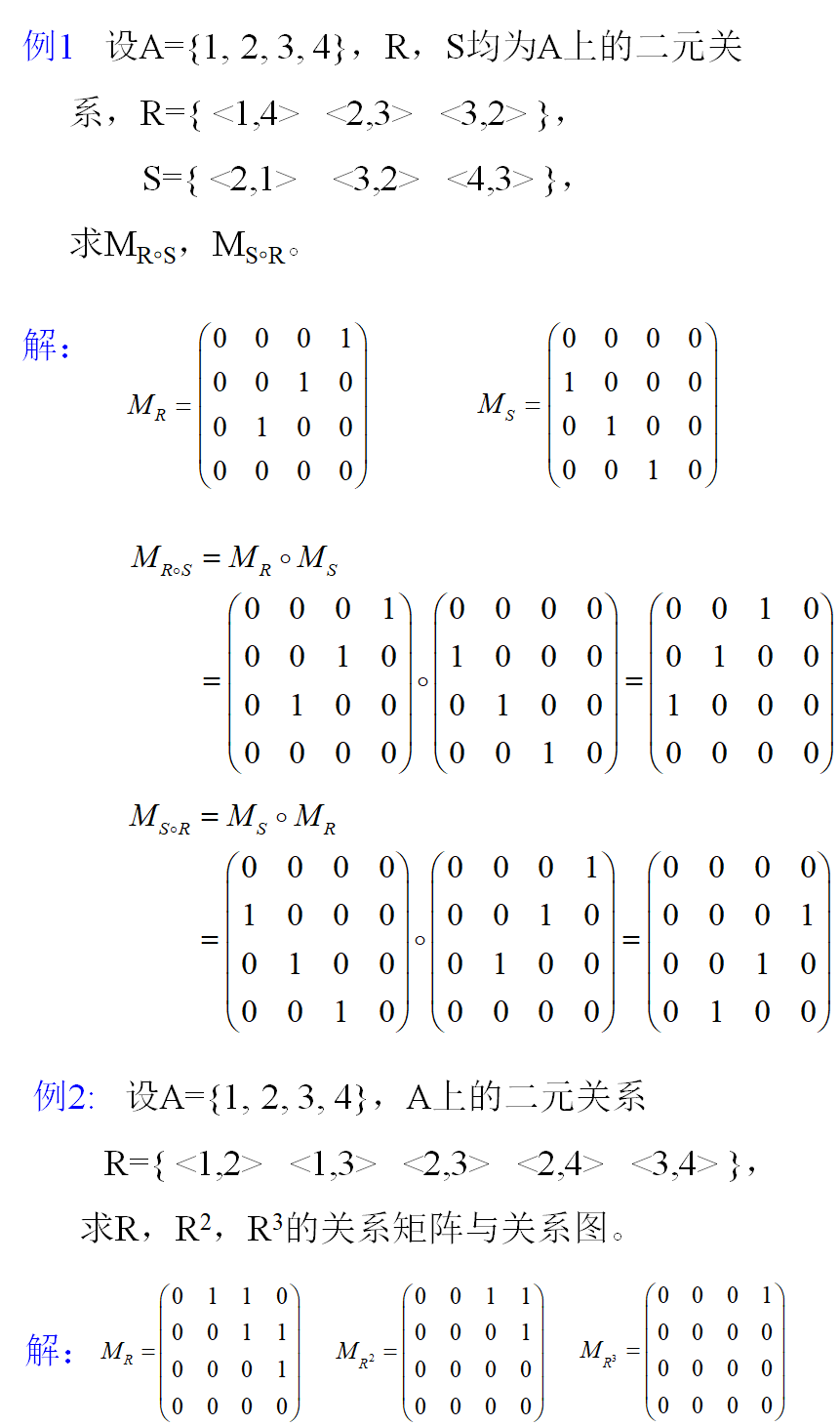
2.6.2 关系 R 的幂

《定义》给定集合X，R 是X上的二元关系， n为自然数，于是 R 的 n 次幂可定义为：
（1） R⁰ = X集合中的恒等关系，即R⁰ ={ <x , x> | x∈X } = I_X ；

（2） Rⁿ⁺¹ = Rⁿ ◦R

设 X = {1 , 2 , 3 }，X上的关系R = { <1,2> <2,3> <3,1> }

         求 R⁰，R²，R³，R⁴。

解： R⁰  = { <1,1> <2,2> <3,3> } = I_X                   R²  = { <1,3> <2,1> <3,2> }

         R³  = R² ◦ R = { <1,1> <2,2> <3,3> } = I_X     R⁴  = R³ ◦ R = R

《定理》设R为A上的二元关系，m，n为自然数，那么

（1）R^mRⁿ  = R^m+n   

（2）(R^m)ⁿ  = R^mn .

设Ａ={a, b, c, d}, R={<a, b> <b, a> <b, c> <c, d>},求 R²，R³ ，R⁴，R⁵。

解：R²  = { <a, a>  < a, c >  < b, b > < b, d > }

         R³  = R² ◦ R = { <a, b> < a, d >  <b, a>   <b, c>}

         R⁴  = R³ ◦ R = {<a, a>   <a, c>   <b, b>   <b, d>} = R² .

 R5  = R4 ◦ R = R2 ◦ R = R3 .

 注：若|X|=n，则X中的二元关系R的幂次值是有限的。一般不用求出超过X的基数次幂。

 

2.6.3逆关系

定义：给定两个集合X和Y，若R 是X→Y的关系，那么从Y→X的关系称为R的逆关系，记为或R^-1，即

⑴只要将R中每一个序偶中的元素全部调换位置，就可得到R的逆关系

(2)的关系矩阵为

⑶ 在R的关系图中，只要把所有箭头改换方向，就可得到的关系图。（自回路箭头改变与否无关)

 

 

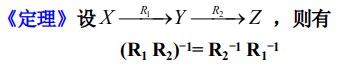
 定理：设R ，R₁，R₂是集合A，B上的二元关系，则

(1) ( R^-1)^-1=R；                    

(2) (R₁∪R₂)^-1=R₁^-1∪R₂^-1；
(3) (R₁∩R₂)^-1=R₁^-1∩R₂^-1  ；           

(4) (R₁-R₂)^-1=R₁^-1 -R₂^-1  ；

(5) (A×B)^-1=B×A;                   

(6) Ø ^-1= Ø；

(7) R₁ ⊆ R₂，则 R₁^-1 ⊆ R₂^-1；

 

定理：设R是X中的二元关系，那么R是对称的当且仅当 R  = 

 

2.6.4关系的闭包

《定义》给定集合X，R是X中的二元关系，若有另一关系 R¢满足下列条件：

         ⑴ R′是自反的（对称的、可传递的）；     

　　  ⑵ R′  ⊇ R ；

         ⑶ 对于任一自反（对称、可传递）关系R″，若R″  ⊇  R ，则必有 R²  ⊇  R′；

         则称R′是R的自反（对称、可传递）闭包，并依次用r(R)，s(R)，t(R)来表示之。

 

讨论定义：

⑴ 已知一个集合中的二元关系R，则 r(R)，s(R)，t(R) 是唯一的，它们是包含R的最小的自反（对称、可传递）关系；

⑵ 若R是自反（对称、可传递）的，则 r(R)，s(R)，t(R) 就是R本身；

⑶ 若R不是自反（对称、可传递）的，则我们可以补上最少序偶，使之变为自反（对称、可传递）关系，从而得到r(R)，s(R)，t(R) .

 

《定理》给定集合X，R是X上的二元关系，则

         ⑴  R是自反的当且仅当  r(R)=R；

         ⑵  R是对称的当且仅当  s(R)=R；

         ⑶  R是可传递的当且仅当  t(R)=R。

 

《定理1》设R是X上的二元关系，I_x 是X上的恒等关系，则有 r(R) = R U I_x  .

《定理2》设R是X上的二元关系，则有 s(R) = R U R^-1

《定理3》设R是X上的二元关系，则有 t(R) = R U R² U R³  U ··· =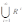

 

 

 

2.6.5次序关系

2.6.5.1偏序集合

定义：

设R是X上的二元关系，如果R是自反的，反对称的和可传递的，则称R是X中的偏序关系（或称偏序），并用符号“≤”表示，而序偶〈X，≤〉则称为偏序集合。

⑴ “≤”不单纯意味着在实数中的 ≤ 关系，而是代表更为普遍的关系（具有自反，反对称和可传递性的关系）；

⑵ 若 x, y∈ X ，“x ≤ y”读作：“x小于或等于y”；

⑶ R是集合X中的偏序关系，则 R 也是X中的偏序关系，若R用“≤”表示，R 则用“≥”表示；

⑷ 若〈X，≤〉是一个偏序集合，则〈X，≥〉也一定是偏序集合，且偏序集合是一个序偶，左元素为集合X，右元素为偏序关系。

定义：在偏序集合〈X，≤〉中，若对任意的 x, y∈X，均有x ≤ y 或 y ≤ x，则称x和y是可比较的，否则称x和 y是不可比较的。

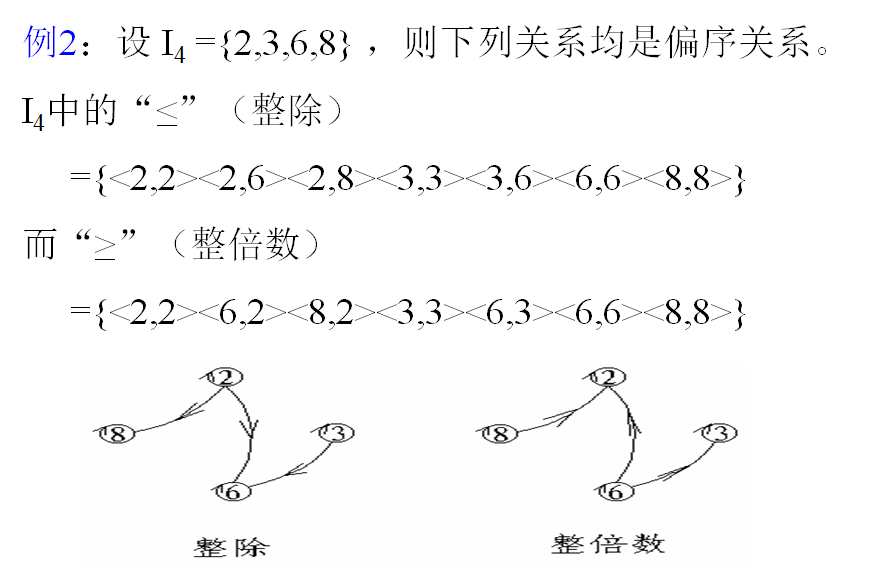
例1：
（1）在领导机构的集合中“领导和被领导的关系”是偏序关系；
（2）在 I（整数）集合中，“≤”、“≥”均是偏序关系；
（3）幂集ρ(A)上的包含关系 “⊆” 是偏序关系；
（4）正整数集 Z+上的整除关系是偏序关系；

 

2.6.5.2特殊的

拟序集合

定义：R是集合X中的二元关系，若R是反自反的，反对称的和可传递的，则称R是X中的拟序关系（串序），并用符号“<”表示。而序偶〈X,<〉称为拟序集合。

讨论：（1）拟序关系一定反对称的；（2）拟序关系也可用偏序关系来定义：

 

 

全序集合

定义：设〈X，≤〉是一个偏序集合，若对于每一个 x, y ∈ X ，或者 x ≤ y，或者 y ≤ x，即

∀x ∀y(x ∈X ∧ y ∈ X → x ≤ y∨y ≤ x) ，则称偏序关系“≤” 为全序关系，

而〈X，≤〉称为全序集合（线序集合）。

 

在偏序集合〈X，≤〉中，若对任意的 x, y∈ X，均有x ≤ y 或 y ≤ x，则称x和y是可比较的，

否则称x和 y是不可比较的。

在偏序集合中，一般情况下，一定是：有的元素是可以比较的，有的元素是不可比较的。

而在全序关系中，所有的元素均是可比较的.

 

良序集合

  定义：若集合X上的二元关系R是全序关系，且X的任一非空子集，都有一个最小元素，

             则称R为良序关系，并称<X,R>为良序集合。

注：⑴ 良序关系比全序关系多了一个条件，即在全序关系中，X集合的任一非空子集均有一个最小元素；

⑵ 每一个有限集合X上的全序关系必定是良序关系。

例如：设集合A={1,2,3,4}，定义A上的全序关系：
“≤” = { <1,1><1,2><1,3><1,4><2,2>
<2,3><2,4><3,3><3,4><4,4> }.
则“≤”也是良序关系。

 

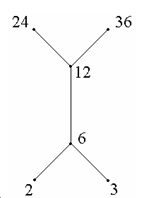
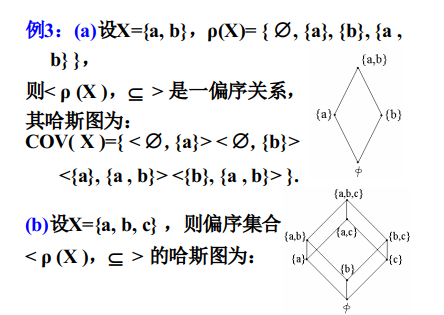
 2.6.5.3偏序集合和哈斯图

2.6.5.3.1定义

在偏序集合〈X，≤〉中，若有 x, y ∈ X，且x ≤ y 但 x ≠ y ，

且又不存在其它元素 z 能使x ≤ z ∧ z ≤ y，

则称元素 y 盖住 x，盖住集记为 COV( X )={< x, y >| x, y ∈  X；y盖住 x }.

给定偏序集合〈X，≤〉，它的盖住集是唯一的。

我们可以画出盖住集的关系图，称为偏序集合〈X，≤〉的哈斯图。

 

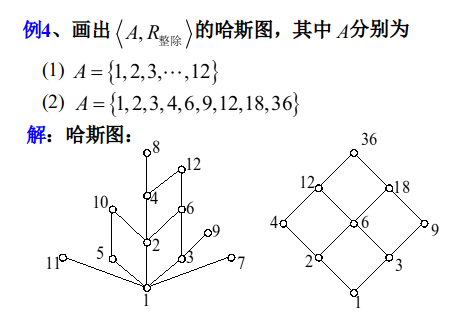
2.6.5.3.2偏序集合〈X，≤〉的哈斯图的画法

⑴ 用“◦”表示 X 中的结点（表示自反性）；

⑵ 若 x, y∈ X ，且 x ≤ y 和 x ≠ y ，则把 x 画在y 的下面；

⑶ 若 y 盖住 x，则在 x 和y之间画一条连线，并箭头向上；若 y 不盖住 x，但又存在“≤”关系，则必定能通过 x 和 y 之间的其它中间结点把 x 和 y 联结起来；

⑷ 所有边的方向均是向上的，所以实际画时，箭头均可省去。

 

 

 

 

 

 

2.6.5.3.3偏序集中的最小（大）元，极小（大）元

《定义》给定偏序集合<A , ≤ >，且子集 B ⊆ A，

(1) 若∃ b∈ B ，使得∀x（ x ∈B → x ≤ b）成立，则称 b 为 B 的最大元，即 b 大于B中其它所有元。

(2) 若∃ b∈ B ，使得∀x（ x ∈B → b ≤ x）成立，则称 b 为 B 的最小元，即 b 小于B中其它所有元。

《定义》给定偏序集合< A , ≤ >，且子集 B ⊆ A，

(1) 若∃ b ∈ B ，使得¬ ∃x（ x ∈B ∧ x ≤ b）成立，则称 b 为 B 的极小元。即B中没有比 b 还小的元。

(2) 若∃ b ∈ B ，使得¬ ∃x（ x ∈B ∧ b ≤ x）成立，则称 b 为 B 的极大元。即B中没有比 b 还大的元。

 

注：由定义可知：

⑴ 集合B的最大（小）元、极大（小）元，若有的话，必在 B 中；

⑵ 最大（小）元是对B中所有元素与其作比较而言的；而极大（小）元是对 B 中能够与其作比较的元素而言的。

⑶ 最大（小）元不一定存在，若存在必唯一；而极大（小）元一定存在，且不一定唯一。

 

 

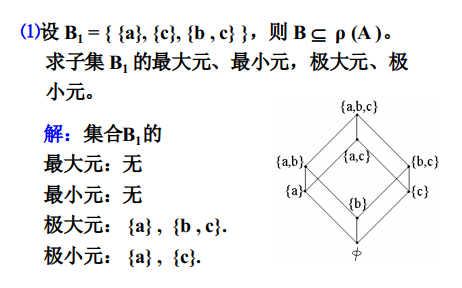
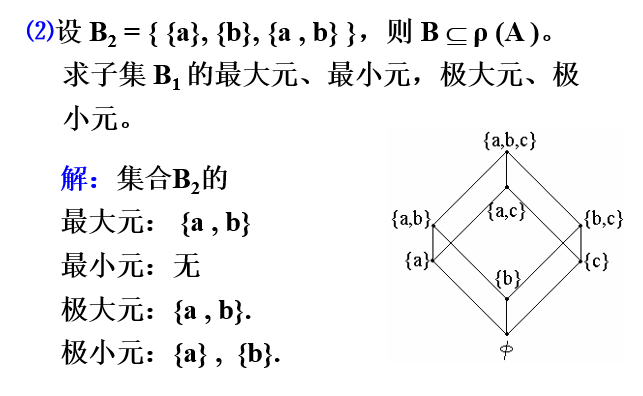
2.6.5.3.4偏序集中的上（下）界，上（下）确界

 定义

给定偏序集合< A , ≤ >，且子集 B ⊆ A，

(1) 若 ∃ a ∈ A ，使得∀x（ x ∈B  → x ≤ a）成立，则称 a 为 B 的上界，其中最小的一个上界，

称为 B 的上确界，记为LUB。

(2) 若 ∃ a ∈ A ，使得∀x（ x ∈B  → a ≤ x）成立，则称 a 为 B 的下界，其中最大的一个下界，

称为 B 的下确界，记为GLB。

 

注：由定义可知：

(1) 上（下）界是与 B 中所有元素作比较而言的。

(2) B 的上（下）界不一定存在，若存在，也不一定是唯一的。

(3) B 的LUB（GLB）不一定存在，若存在必唯一。

(4) 若B 的上（下）界、LUB（GLB）存在，则其可能在B 中，

也可能不在 B 中，但一定在 A中。

 

《定理》设偏序集合 < A , ≤ >，B是A的子集，则：

         (1) 如果b是B的最大元，那么b也是B的极大元.

         (2) 如果b是B的最大元，那么b就是B的 lub.

         (3) 如果b是B的一个上界且 b ∈ B，那么b就是B的最大元.

 

 

2.6.5等价关系

2.6.5.1定义

　　设R是X上的二元关系，如果R是自反的、对称的和可传递的，

        则称R是X上的等价关系。

        若 <x , y>∈  R，则记为 x ~ y .

分析：等价关系R的有向图满足：自反的，对称的，传递的。

例1：下列关系均为等价关系
（1）实数集合上的“=”关系；
（2）{人类} 中的同姓关系；
（3）命题集合上的等价关系；
（4）三角形的全等关系，三角形的相似关系是等价关系；
（5）在一个班级里“年龄相等”的关系是等价关系；

 

2.6.5.2等价类

　　定义：设R是X上的等价关系，对于∀ x ∈ X ，定义 X 的子集

[x]_R = { y | y ∈ X∧ x R y }

称子集 [x]_R是由 x 生成的关于R的等价类，简记为 [x]，

并称 x 为等价类 [x] 的表示元素。

　

注：⑴ 等价类 [x]_R 是一个集合，且 [x]_R ⊆ X .

　　⑵ [x]_R中的元素是：所有与 x 具有等价关系 R 的元素所组成的集合，且 [x]_R ≠ Ø.

 

 

 

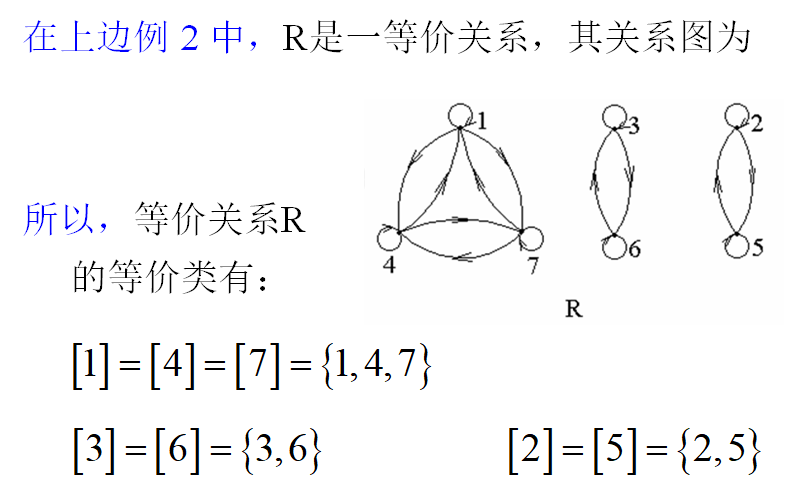
2.6.5.3划分

定义：设X是一非空集合，A₁, A₂ , … , A_m 是它的非空子集，且满足

         ⑴  A_i ∩ A_j = Ø（i ≠ j）；

　　  ⑵  A₁ U A₂ U … U A_m = X；

         则称集合族π ={ A₁, A₂ , … , A_m } 为集合X的一个划分。

         而子集A1, A2 , … , Am 称为这个划分的块。

 

 

定理：设X是一非空集合，R是X中的等价关系，

           则 R 的等价类集合{ [x]_R | x∈ X }就是X的一个划分，

　　    且称此集合为X在R下的商集，记为，即X/R = { [x]_R | x∈ X } .

 

 

 

 

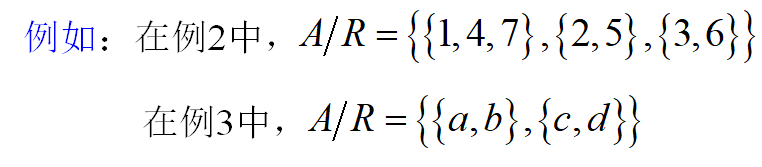
 传递1：https://blog.csdn.net/qq_41705423/article/details/79503938