149.集合论

集合论是研究集合一般性质的数学分支，它的创始人是康托尔

现代数学中，每个对象(如数，函数等)本质上都是集合，都可以用某种集合来定义，数学的各个分支，本质上都是在研究某种对象集合的性质。集合论已成为现代全部数学的理论基础。

集合论的特点是研究对象的广泛性，它总结出由各种对象构成的集合的共同性质，并用统一的方法来处理。因此，集合论被广泛地应用于各种科学和技术领域。

由于集合论的语言适合于描述和研究离散对象及其关系，所以它也是计算机科学与工程的理论基础，而且在程序设计，数据结构，形式语言，关系数据库，操作系统等都有重要应用。

 

1.集合

1.1定义

集合：具有某种特殊性质的客体的聚合。

集合用大写的字母标记，
例如：A、B、C……

元素：属于任何集合的任何客体。

元素用小写字母标记，
例如：a、b、c、……

 

注意：

①元素与集合间的关系： 若 a 是集合 S 中的元素，则可写成 a∈ S ；

　若b不是集 S 合中的元素，则可写成 b∈ S 。

②集合 S 的基数(势)：S中的元素个数。记为 |S| .

③有限集合：集合的基数（元素）是有限的。

    无限集合：集合的基数（元素）是无限的。

 

常用集合符：

I_m (m≥1)         有限个正数的集合{1,2,3……m}

N_m (m≥0)        有限个自然数的集合{0,1,2……m}

以上是有限集合,下面是无限集合：

N      自然数集合{0,1,2……}

I+     正整数集合{1,2,3……}

I       整数集合 {……-1,0,1,2……}

P      素数集合 {大于1的正整数，只能被1和自己整除}

Q      有理数集合{  i/j.  i、j均为整数且 j≠0 }

R      实数集合 {有理数、无理数}

C      复数集合{a + bi，a、b可为实数 i = √-1 }

 

1.2集合的表示法

(1) 列举法  (将元素一一列出)

(2) 描述法  (用谓词概括元素的属性)

　　所有集合均可用谓词公式来表示 

　　　　注：同一集合可以用多种不同的形式表示。集合也可作为某一集合的元素。例如：S={ a，{1,2}，p，{q} }

(3) 文氏图  文氏图的画法规则：规定矩形表示E。子集用圆画在E中。

　　　　文氏图应用：（a）表示集合和运算的关系，可用文氏图画出各种运算（b）证明集合恒等式

 

1.3集合间的关系

（1）B为A的子集 B⊆A ；B为A的真子集 B⊂A
　　  B⊆A⇔∀x(x∈B→x∈A)     B⊄A⇔∃x(x∈B∧x∉A)
（2）集合A，B相等A=B     A=B⇔A⊆B∧B⊆A
（3）对任意集合A有A⊆A
（4）对任意集合A，有∅⊆A⊆E

 

1.4特殊集合：空集、全集合、集合族

 

全集：如果一个集合包含了所要讨论的每一个集合，则称该集合为全集合，简称全集，用 E表示。

E={x | P(x)∨ ¬P(x) } P(x)为任何谓词公式.

 

空集：不拥有任何元素的集合称为空集（或称零集），用Ø表示，

Ø ={x | P(x)∧¬P(x) } = { }

注意：Ø ≠ {Ø} 前者是空集，是没有元素的集合；后者是以Ø作为元素的集合。

 

集合族：集合中的元素均为集合，称这样的集合为集合族。

例如A={{a}，{b}，{c、d}}

 

幂集：设A是集合，以A的所有子集作为元素的集合称为A的幂集。记作 ρ(A) 或 2^A ,

且有：ρ(A) = {x | x ∈A}   例如：若A1={a}，则 ρ(A1)={Φ ，{a}} 若A3=Ø，则  ρ(A3)={Ø}

讨论定义：

(a) 集合的元素个数称为集合的“基数”或叫“势”    |ρ(S)|=2 ^|s| 为幂集ρ(S)的基数

(b) 若A为有限集合，则ρ(A)也为有限集合。若A为无限集合，则ρ(A)也为无限集合。

(c) 一定有A∈ρ(A)，Ø∈ρ(A)，即对非空集合A，在幂集中至少有两个子集Ø和A。

 

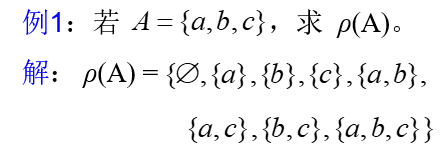
索引集合：为了在计算机上表示集合，必须给每一个集合的元素加上标记，以用来表示元素在集合中的位置。

例如：S={a，b} 假设集合S中，a , b的位置已经固定。

则用二进制下标法来表示S的所有子集： Ø ={ }=B₀₀，{a}=B₁₀，{b}=B₀₁，{a，b}=B₁₁

这样ρ(S)={B₀₀，B₀₁，B₁₀，B₁₁}={B_i | i ∈ J}

其中J={00，01，10，11} （索引集合或指标集合）

 

笛卡尔乘积

1、定义

设A，B为二个任意集合，若序偶的第一个成员（左元素）是A的一个元素，序偶的第二个成员（右元素）是B的一个元素，则所有这样的序偶的集合称为A和B的笛卡尔乘积。

记作：A×B = {〈x，y〉|  (x ∈A) ∧ (y ∈B)  }       “×”不满足结合律。

 

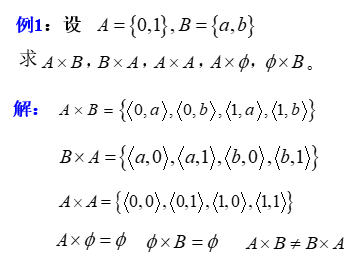
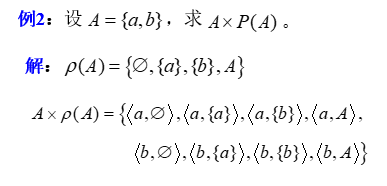
n个集合的笛卡儿乘积的定义：

A₁×A₂×...×A_n={⟨x₁,x₂,⋯,x_n ⟩|x₁∈A₁∧x₂∈A₂∧⋯∧x_n∈A_n 

当时A₁=A₂=⋯=A_n=A时，记为 Aⁿ 

 A={a,b}    A²={⟨a,a⟩,⟨a,b⟩,⟨b,a⟩,⟨b,b⟩}

 

2、笛卡儿积运算对∪和 ∩ 满足分配律

若A，B，C是三个集合，则有：

A×(B∪C)=(A×B)∪(A×C)

(B∪C)×A=(B×A)∪(C×A)

A×(B∩C)=(A×B)∩(A×C)

(B∩C)×A=(B×A)∩(C×A)

注意：  

（1）若A是m元集，B是n元集，则A×B为mn元集

（2）笛卡儿积是集合，有关集合的运算都适合。

（3）笛卡儿积不满足交换律，即 A×B ≠ B×A.

（4）笛卡儿积不满足结合律，即 （A×B）×C ≠ A×（B×C）

 

 

 1.5 集合的运算

 集合运算律