python-torch numpy matploit pandas
numpy
数组对象是 NumPy 中最核心的组成部分,这个数组叫做 ndarray,是“N-dimensional array”的缩写。其中的 N 是一个数字,指代维度. 在 NumPy 中,数组是由 numpy.ndarray 类来实现的,它是 NumPy 的核心数据结构。
而 Python 中的列表,其实也可以达到与 NumPy 数组相同的功能,但它们又有差异,做个对比你就能体会到 NumPy 数组的特点了。
-
1.
Python中的列表可以动态地改变,而NumPy数组是不可以的,它在创建时就有固定大小了。改变Numpy数组长度的话,会新创建一个新的数组并且删除原数组。 -
2.
NumPy数组中的数据类型必须是一样的,而列表中的元素可以是多样的。 -
3.
NumPy针对NumPy数组一系列的运算进行了优化,使得其速度特别快,并且相对于 Python 中的列表,同等操作只需使用更少的内存。创建数组
最简单的方法就是把一个列表传入到 np.array() 或 np.asarray() 中,这个列表可以是任意维度的。np.array() 属于深拷贝,np.asarray() 则是浅拷贝.
代码如下
>>>import numpy as np>>>
#引入一次即可
>>>arr_1_d = np.asarray([1])
>>>print(arr_1_d)[1]
>>>arr_2_d = np.asarray([[1, 2], [3, 4]])
>>>print(arr_2_d)
[[1 2]
[3 4]]
数组的属性
ndim
ndim 表示数组维度(或轴)的个数。刚才创建的数组 arr_1_d 的轴的个数就是 1,arr_2_d 的轴的个数就是 2。
>>>arr_1_d.ndim
1
>>>arr_2_d.ndim
2
shape
shape 表示数组的维度或形状, 是一个整数的元组,元组的长度等于 ndim。arr_1_d 的形状就是(1,)(一个向量), arr_2_d 的形状就是 (2, 2)(一个矩阵)。
>>>arr_1_d.shape
(1,)
>>>arr_2_d.shape
(2, 2)
shape 这个属性在实际中用途还是非常广的。比如说,我们现在有这样的数据 (B, W, H, C),这代表一个 batch size 为 B 的(W,H,C)数据.
现在我们需要根据(W,H,C)对数据进行变形或者其他处理,这时我们可以直接使用 input_data.shape[1:3]
在实际的工作当中,我们经常需要对数组的形状进行变换,就可以使用 arr.reshape() 函数,在不改变数组元素内容的情况下变换数组的形状。但是你需要注意的是,变换前与变换后数组的元素个数需要是一样的
>>>arr_2_d.shape
(2, 2)
>>>arr_2_d
[[1 2]
[3 4]]
# 将arr_2_d reshape为(4,1)的数组
>>>arr_2_d.reshape((4,1))
array([[1],
[2],
[3],
[4]])
我们还可以使用 np.reshape(a, newshape, order) 对数组 a 进行 reshape,新的形状在 newshape 中指定。
这里需要注意的是,reshape 函数有个 order 参数,它是指以什么样的顺序读写元素,其中有这样几个参数。
-
‘C’:默认参数,使用类似 C-like 语言(行优先)中的索引方式进行读写。
-
‘F’:使用类似 Fortran-like 语言(列优先)中的索引方式进行读写。
-
‘A’:原数组如果是按照‘C’的方式存储数组,则用‘C’的索引对数组进行 reshape,否则使用’F’的索引方式reshape 的过程你可以这样理解,首先需要根据指定的方式 (‘C’或’F’) 将原数组展开,然后再根据指定的方式写入到新的数组中。这是什么意思呢?先看一个简单的 2 维数组的例子。
数组a,按照’F’的方式 reshape 成 (3,2) 要如何处理。对于行优先的方式,我们应该是比较熟悉的,而‘F’方式是列优先的方式。首先是按列优先展开原数组,列优先意味着最先变化的是数组的第一个维度。下表是展开后的结果,序号是展开顺序,这里请注意下坐标的变换方式(第一个维度最先变化)
>>>a = np.arange(6).reshape(2,3)
array([[0, 1, 2],
[3, 4, 5]])
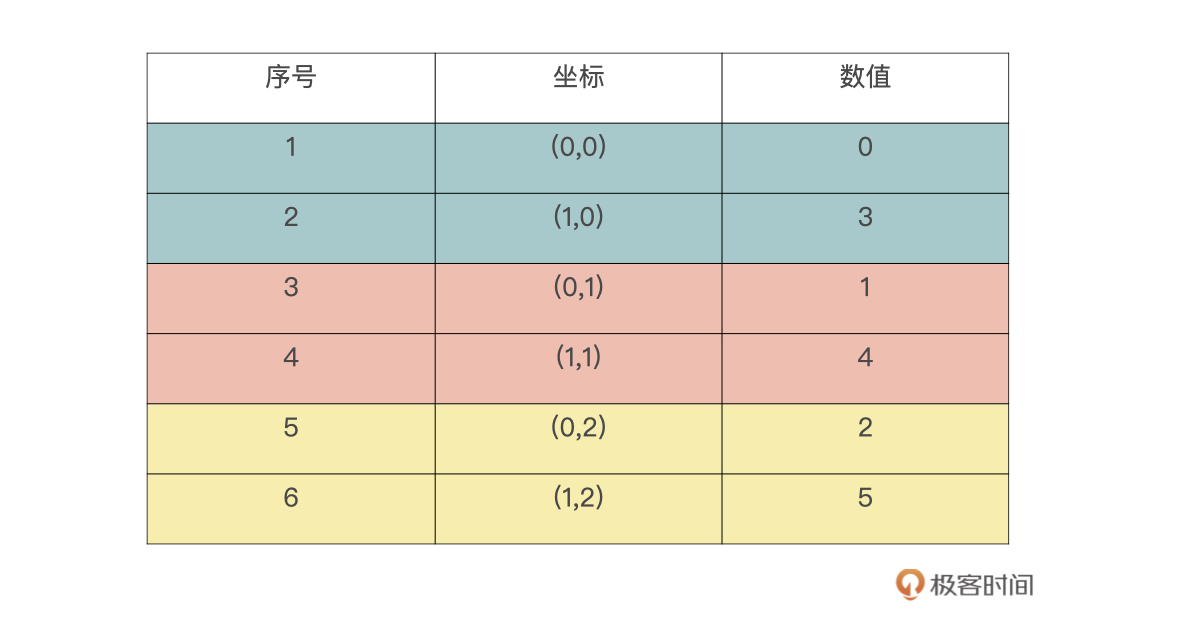
所以,reshape 后的数组,是按照 0,3,1,4,2,5 这个序列进行写入数据的。reshape 后的数组如下表所示,序号代表写入顺序
size
size,也就是数组元素的总数,它就等于 shape 属性中元素的乘积。
dtype
数组的数据类型当然也可以改变,我们可以使用 astype() 改变数组的数据类型,不过改变数据类型会创建一个新的数组,而不是改变原数组的数据类型。
>>>arr_2_d.dtype
dtype('float64')
>>>arr_2_d.astype('int32')
array([[1, 2],
[3, 4]], dtype=int32)
>>>arr_2_d.dtype
dtype('float64')
# 原数组的数据类型并没有改变
>>>arr_2_d_int = arr_2_d.astype('int32')
>>>arr_2_d_int.dtype
dtype('int32')
其他创建数组的方式
np.ones() 与 np.zeros()
>>>np.ones()
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: ones() takes at least 1 argument (0 given)
# 报错原因是没有给定形状的参数
>>>np.ones(shape=(2,3))
array([[1., 1., 1.],
[1., 1., 1.]])
>>>np.ones(shape=(2,3), dtype='int32')
array([[1, 1, 1],
[1, 1, 1]], dtype=int32)
那这两个函数一般什么时候用呢?例如,如果需要初始化一些权重的时候就可以用上,比如说生成一个 2x3 维的数组,每个数值都是 0.5,可以这样做。
>>>np.ones((2, 3)) * 0.5
array([[0.5, 0.5, 0.5],
[0.5, 0.5, 0.5]]
np.linspace()
最后,我们也可以用 np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)创建一个数组,具体就是创建一个从开始数值到结束数值的等差数列。
-
start:必须参数,序列的起始值。
-
stop:必须参数,序列的终点。
-
num:序列中元素的个数,默认是 50。
-
endpoint:默认为 True,如果为 True,则数组最后一个元素是 stop。
-
retstep:默认为 False,如果为 True,则返回数组与公差。
# 从2到10,有3个元素的等差数列 >>>np.linspace(start=2, stop=10, num=3)
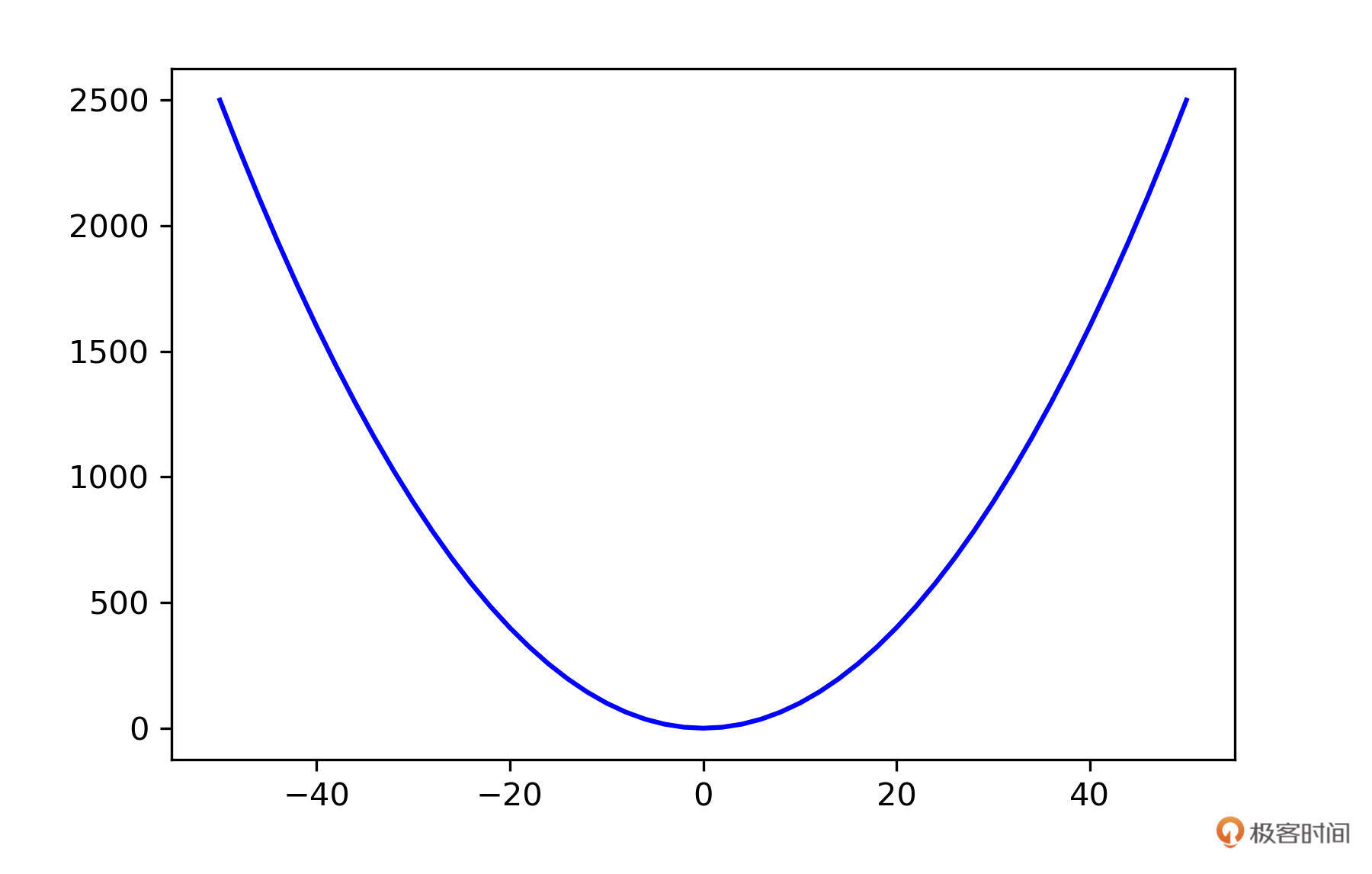
np.arange 与 np.linspace 也是比较常见的函数,比如你要作图的时候,可以用它们生成 x 轴的坐标。例如,我要生成一个 y=x^2 的图片,x 轴可以用 np.linespace() 来生成。
import numpy as np
import matplotlib.pyplot as plt
X = np.arange(-50, 51, 2)
Y = X ** 2
plt.plot(X, Y, color='blue')
plt.legend()
plt.show()
数组的轴
超级重要
它经常出现在 np.sum()、np.max() 这样关键的聚合函数中。
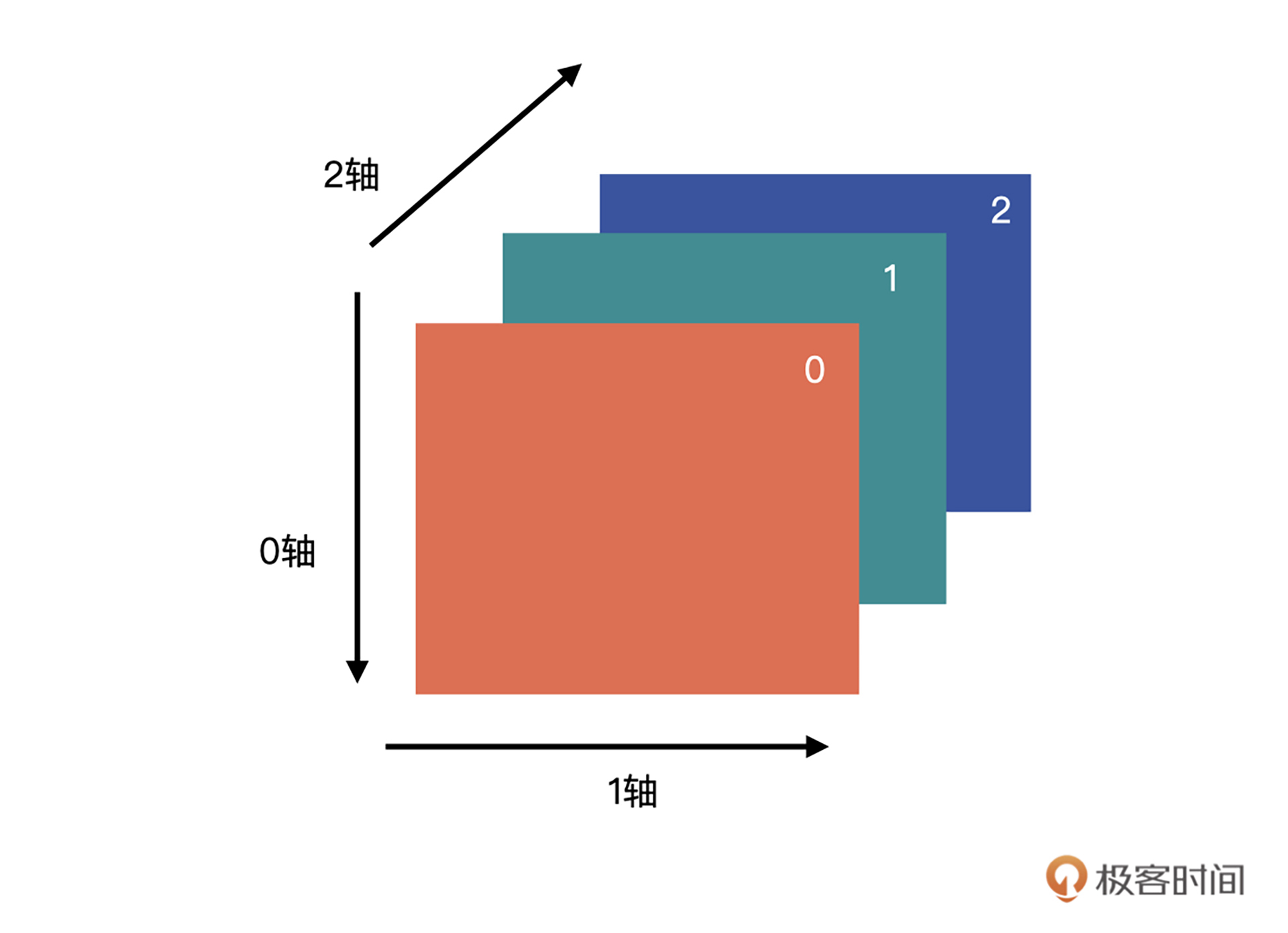
问题:同一个函数如何根据轴的不同来获得不同的计算结果呢?比如现在有一个 (4,3) 的矩阵,存放着 4 名同学关于 3 款游戏的评分数据。
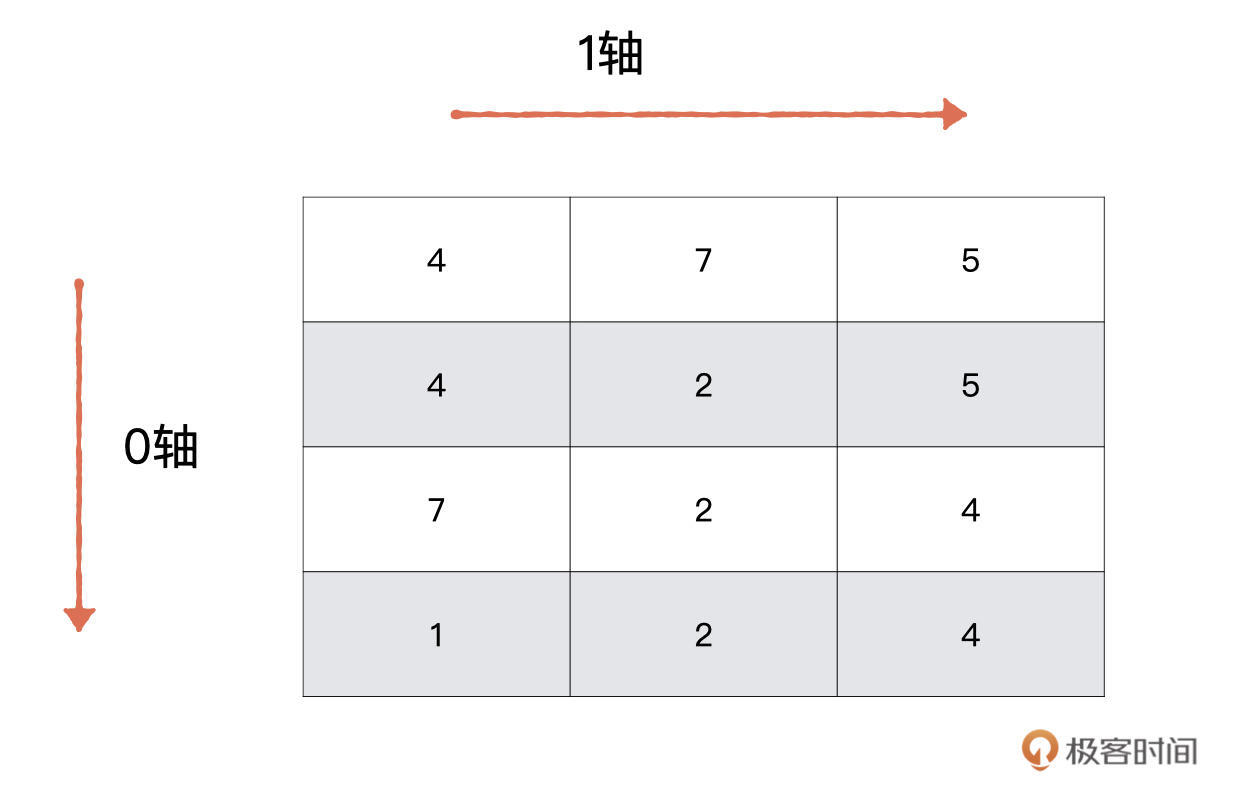
第一个需求是,计算每一款游戏的评分总和。这个问题如何解决呢,我们一起分析一下。数组的轴即数组的维度,它是从 0 开始的。对于我们这个二维数组来说,有两个轴,分别是代表行的 0 轴与代表列的 1 轴。如下图所示。
第二个问题是要计算每名同学的评分总和,也就是要沿着 1 轴方向对二维数组进行操作。所以,我们只需要将 axis 参数设定为 1 即可。
>>>interest_score = np.random.randint(10, size=(4, 3))
>>>interest_score
array([[4, 7, 5],
[4, 2, 5],
[7, 2, 4],
[1, 2, 4]])
>>> np.sum(interest_score, axis=0)
array([16, 13, 18])
# 沿着行的‘方向’
>>> np.sum(interest_score, axis=1)
array([16, 11, 13, 7])
# 沿着列的‘方向’
二维数组还是比较好理解的,那多维数据该怎么办呢?其实当 axis=i 时,就是按照第 i 个轴的方向进行计算的,或者可以理解为第 i 个轴的数据将会被折叠或聚合到一起。
形状为 (a, b, c) 的数组,沿着 0 轴聚合后,形状变为 (b, c);沿着 1 轴聚合后,形状变为 (a, c);沿着 2 轴聚合后,形状变为 (a, b);更高维数组以此类推。
接下来,我们再看一个多维数组的例子。对数组 a,求不同维度上的最大值
>>> a = np.arange(18).reshape(3,2,3)
>>> a
array([[[ 0, 1, 2],
[ 3, 4, 5]],
[[ 6, 7, 8],
[ 9, 10, 11]],
[[12, 13, 14],
[15, 16, 17]]])

我们可以将同一个轴上的数据看做同一个单位,那聚合的时候,我们只需要在同级别的单位上进行聚合就可以了。如上图所示,绿框代表沿着 0 轴方向的单位,蓝框代表着沿着 1 轴方向的单位,红框代表着 2 轴方向的单位。
- 当 axis=0 时,就意味着将三个绿框的数据聚合在一起,结果是一个(2,3)的数组,数组内容为:

>>> a.max(axis=0)
array([[12, 13, 14],
[15, 16, 17]])
- 当 axis=1 时,就意味着每个绿框内的蓝框聚合在一起,结果是一个(3,3)的数组,数组内容为:
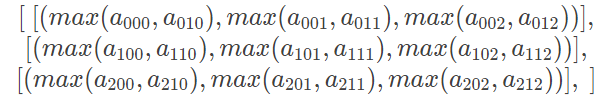
>>> a.max(axis=1) //相当于向下投影
array([[ 3, 4, 5],
[ 9, 10, 11],
[15, 16, 17]])
当 axis=2 时,就意味着每个蓝框中的红框聚合在一起,结果是一个(3,2)的数组
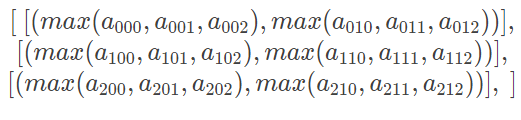
>>> a.max(axis=2)
array([[ 2, 5],
[ 8, 11],
[14, 17]])
- axis 参数非常常见,不光光出现在刚才介绍的 sum 与 max,还有很多其他的聚合函数也会用到,例如 min、mean、argmin(求最小值下标)、argmax(求最大值下标)等。
数据加载阶段
这个阶段我们要做的就是把训练数据读进来,然后给模型训练使用。训练数据不外乎这三种:图片、文本以及类似二维表那样的结构化数据。
不管使用PyTorch还是 TensorFlow,或者是传统机器学习的 scikit-learn,我们在读入数据这一块,都会先把数据转换成NumPy的数组,然后再进行后续的一系列操作。
对应到我们这个项目中,需要做的就是把训练集中的图片读入进来。对于图片的处理,我们一般会使用 Pillow 与 OpenCV 这两个模块。虽然 Pillow 和 OpenCV 功能看上去都差不多,但还是有区别的。
在 PyTorch 中,很多图片的操作都是基于 Pillow 的,所以当使用 PyTorch 编程出现问题,或者要思考、解决一些图片相关问题时,要从 Pillow 的角度出发。下面我们先以单张图片为例,将极客时间的那张 Logo 图片分别用 Pillow 与 OpenCV 读入,然后转换为NumPy的数组。
Pillow 方式
Pillow 是以二进制形式读入保存的,我们只需要利用 NumPy 的 asarray 方法,就可以将 Pillow 的数据转换为 NumPy 的数组格式。
from PIL import Image
im = Image.open('jk.jpg')
im.size
输出: 318, 116
im_pillow = np.asarray(im)
im_pillow.shape
输出:(116, 318, 3)

OpenCV 方式:
OpenCV 的话,不再需要我们手动转格式,它直接读入图片后,就是以 NumPy 数组的形式来保存数据的,如下面的代码所示。
import cv2
im_cv2 = cv2.imread('jk.jpg')
type(im_cv2)
输出:numpy.ndarray
im_cv2.shape
输出:(116, 318, 3)
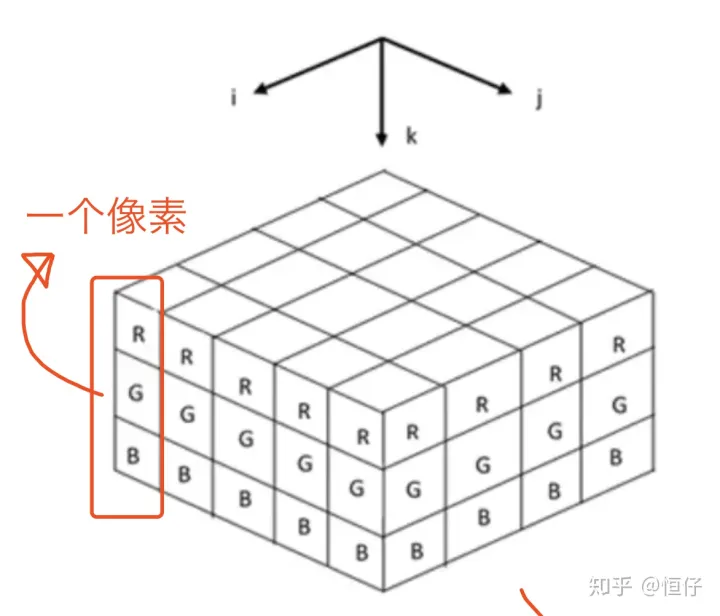
结合代码输出可以发现,我们读入后的数组的最后一个维度是 3,这是因为图片的格式是 RGB 格式,表示有 R、G、B 三个通道。对于计算视觉任务来说,绝大多数处理的图片都是 RGB 格式,如果不是 RGB 格式的话,要记得事先转换成 RGB 格式。这里有个地方需要你关注,Pillow 读入后通道的顺序就是 R、G、B,而 OpenCV 读入后顺序是 B、G、R。
RGB 三个通道各有 256 个亮度,分别用数字 0 到 255 表示,数字越高代表亮度越强,数字 0 则是代表最弱的亮度。在我们的例子中,如果一个通道的数据再加另外两个全 0 的通道(相当于关闭另外两个通道),最终图像以红色格调(可以先看一下后文中的最终输出结果)呈现出来的话,我们就可以认为该通道的数据是来源于 R 通道,G 与 B 通道的证明同样可以如此。
im_pillow[:, :, 0]
- 上述代码的含义就是取第三个维度索引为 0 的全部数据,换句话说就是,取图片第 0 个通道的所有数据。(下图是个俯视图需要注意)。

im_pillow_c1 = im_pillow[:, :, 0]
im_pillow_c2 = im_pillow[:, :, 1]
im_pillow_c3 = im_pillow[:, :, 2]注意这里的轴和torch中的还是有不同的
这样的话,通过下面的代码,我们就可以获得每个通道的数据了。
获得了每个通道的数据,接下来就需要生成一个全 0 数组,该数组要与 im_pillow 具有相同的宽高。
# 然后,我们只需要将全 0 的数组与 im_pillow_c1、im_pillow_c2、im_pillow_c3 进行拼接,就可以获得对应通道的图像数据了。
zeros = np.zeros((im_pillow.shape[0], im_pillow.shape[1], 1))
zeros.shape
输出:(116, 318, 1)
数组的拼接
刚才我们拿到了单独通道的数据,接下来就需要把一个分离出来的数据跟一个全 0 数组拼接起来。如下图所示,红色的可以看作单通道数据,白色的为全 0 数据。
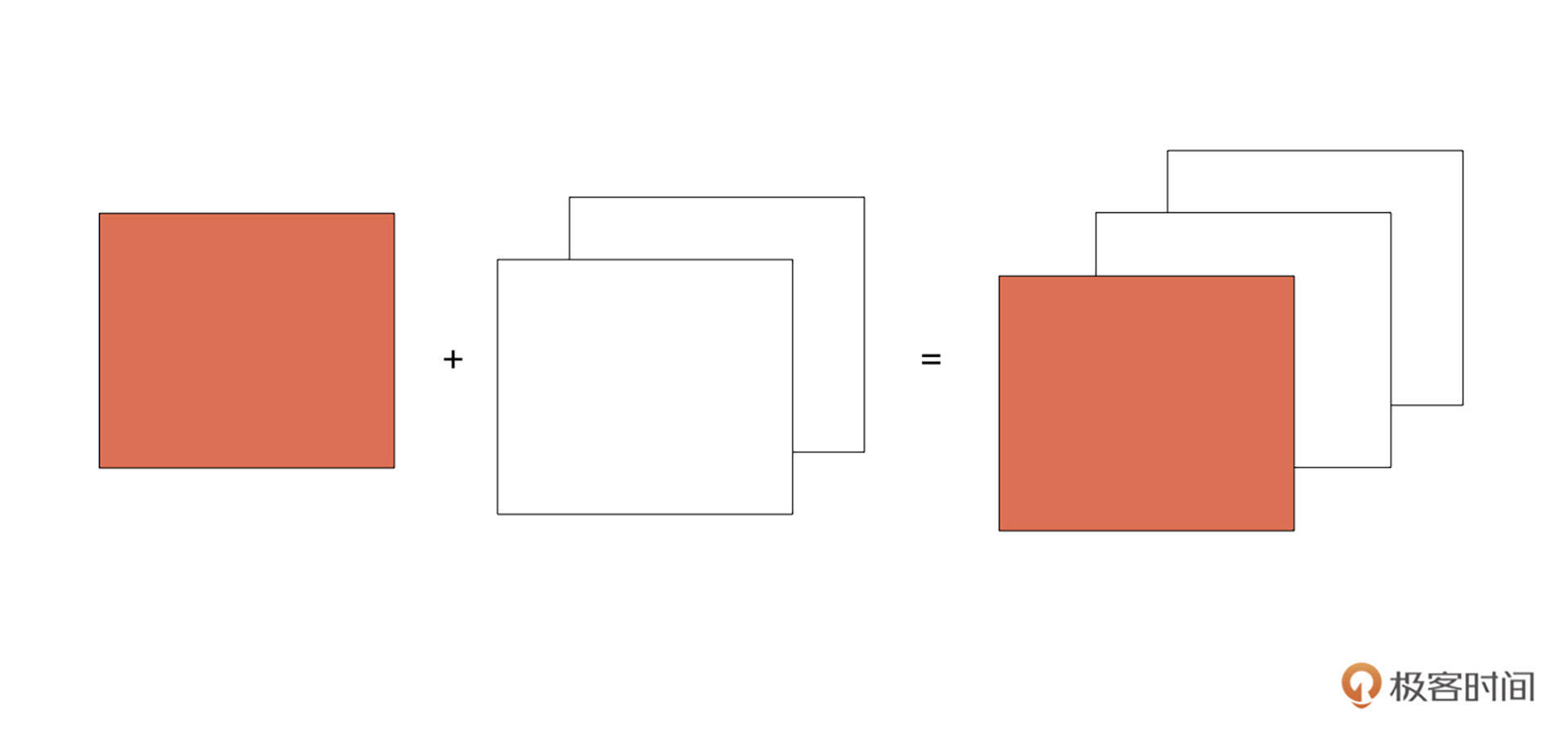
NumPy 数组为我们提供了 np.concatenate((a1, a2, …), axis=0) 方法进行数组拼接。
其中,a1,a2, …就是我们要合并的数组;
axis 是我们要沿着哪一个维度进行合并,默认是沿着 0 轴方向。对于我们的问题,是要沿着 2 轴的方向进行合并,也是我们最终的目标是要获得下面的三幅图像。
zeros = np.zeros((im_pillow.shape[0], im_pillow.shape[1], 1))
zeros.shape
输出:(116, 318, 1)
im_pillow_c1.shape
输出:(116, 318)
注意图像的合并是从最上面开始,所以要以2轴为方向
我们要合并的两个数组维度不一样,需要将 im_pillow_c1 变成 (116, 318, 1) 即可。
方法一:使用 np.newaxis
我们可以使用 np.newaxis 让数组增加一个维度,使用方式如下。
im_pillow_c1 = im_pillow_c1[:, :, np.newaxis]
im_pillow_c1.shape
输出:(116, 318, 1)
运行上面的代码,就可以将 2 个维度的数组转换为 3 个维度的数组了。
这个操作在你看深度学习相关代码的时候经常会看到,只不过 PyTorch 中的函数名 unsqueeze(), TensorFlow 的话是与 NumPy 有相同的名字,直接使用 tf.newaxis 就可以了。
然后我们再次将 im_pillow_c1 与 zeros 进行合并,这时就不会报错了,代码如下所示:
im_pillow_c1_3ch = np.concatenate((im_pillow_c1, zeros, zeros),axis=2)
im_pillow_c1_3ch.shape
输出:(116, 318, 3)
方法二:直接赋值
增加维度的第二个方法就是直接赋值,其实我们完全可以生成一个与 im_pillow 形状完全一样的全 0 数组,
然后将每个通道的数值赋值为 im_pillow_c1、im_pillow_c2 与 im_pillow_c3 就可以了。我们用这种方式生成上图中的中间与右边图像的数组。
im_pillow_c2_3ch = np.zeros(im_pillow.shape)im_pillow_c2_3ch[:,:,1] = im_pillow_c2im_pillow_c3_3ch = np.zeros(im_pillow.shape)im_pillow_c3_3ch[:,:,2] = im_pillow_c3
深拷贝(副本)与浅拷贝(视图)
说到 copy() 的话,就要说到浅拷贝与深拷贝的概念,上节课我们说到创建数组时就提过,np.array() 属于深拷贝,np.asarray() 则是浅拷贝。
简单来说,浅拷贝或称视图,指的是与原数组共享数据的数组,请注意,只是数据,没有说共享形状。视图我们通常使用 view() 来创建。常见的切片操作也会返回对原数组的浅拷贝。
请看下面的代码,数组 a 与 b 的数据是相同的,形状确实不同,但是修改 b 中的数据后,a 的数据同样会发生变化。
a = np.arange(6)
print(a.shape)
输出:(6,)
print(a)
输出:[0 1 2 3 4 5]
b = a.view()
print(b.shape)
输出:(6,)
b.shape = 2, 3
print(b)
输出:[[0 1 2]
[3 4 5]]
b[0,0] = 111
print(a)
输出:[111 1 2 3 4 5]
print(b)
输出:[[111 1 2]
[ 3 4 5]]
而深拷贝又称副本,也就是完全复制原有数组,创建一个新的数组,修改新的数组不会影响原数组。深拷贝使用 copy() 方法。 所以,我们将刚才报错的程序修改成下面的形式就可以了。
# 其实我们还有一种更加简单的方式获得三个通道的 BGR 数据,只需要将图片读入后,直接将其中的两个通道赋值为 0 即可。代码如下所示
from PIL import Image
import numpy as np
im = Image.open('jk.jpg')
im_pillow = np.asarray(im)im_pillow[:,:,1:]=0
输出:---------------------------------------------------------------------------ValueError Traceback (most recent call last) in 4 im = Image.open('jk.jpg') 5 im_pillow = np.asarray(im)----> 6 im_pillow[:,:,1:-1]=0
ValueError: assignment destination is read-only
im_pillow = np.array(im)
im_pillow[:,:,1:]=0
模型评估
Argmax Vs Argmin:求最大 / 最小值对应的索引
NumPy 的argmax(a, axis=None)方法可以为我们解决求最大值索引的问题。如果不指定 axis,则将数组默认为 1 维。
Argsort:数组排序后返回原数组的索引
probs = np.array([0.075, 0.15, 0.075, 0.15, 0.0, 0.05, 0.05, 0.2, 0.25])
我们可以借助 argsort(a, axis=-1, kind=None) 函数来解决该问题。np.argsort 的作用是对原数组进行从小到大的排序,返回的是对应元素在原数组中的索引。
np.argsort 包括后面这几个关键参数:
- a 是要进行排序的原数组;
- axis 是要沿着哪一个轴进行排序,默认是 -1,也就是最后一个轴;
- kind 是采用什么算法进行排序,默认是快速排序,还有其他排序算法,具体你可以看看数据结构的排序算法。
probs_idx_sort = np.argsort(-probs) #注意,加了负号,是按降序排序
probs_idx_sort
输出:array([8, 7, 1, 3, 0, 2, 5, 6, 4])
#概率最大的前三个值的坐标
probs_idx_sort[:3]
输出:array([8, 7, 1])
Torch
PyTorch 中我们称之为张量 (Tensor)。
从标量、向量和矩阵的关系来看,你可能会觉得它们就是不同“维度”的 Tensor,这个说法对,也不全对。说它不全对是因为在 Tensor 的概念中,我们更愿意使用 Rank(秩)来表示这种“维度”,比如标量,就是 Rank 为 0 阶的 Tensor;向量就是 Rank 为 1 阶的 Tensor;矩阵就是 Rank 为 2 阶的 Tensor。也有 Rank 大于 2 的 Tensor。当然啦,你如果说维度其实也没什么错误,平时很多人也都这么叫。
Tensor 的创建
1.直接创建
torch.tensor(data, dtype=None, device=None,requires_grad=False)
结合代码,我们看看其中的参数是什么含义。
-
我们从左往右依次来看,首先是 data,也就是我们要传入模型的数据。PyTorch 支持通过 list、 tuple、numpy array、scalar 等多种类型进行数据传入,并转换为 tensor。
-
接着是 dtype,它声明了你需要返回一个怎样类型的 Tensor,具体类型可以参考前面表格里列举的 Tensor 的 8 种类型。
-
然后是 device,这个参数指定了数据要返回到的设备,目前暂时不需要关注,缺省即可。
-
最后一个参数是 requires_grad,用于说明当前量是否需要在计算中保留对应的梯度信息。在 PyTorch 中,只有当一个 Tensor 设置 requires_grad 为 True 的情况下,才会对这个 Tensor 以及由这个 Tensor 计算出来的其他 Tensor 进行求导,然后将导数值存在 Tensor 的 grad 属性中,便于优化器来更新参数。所以,你需要注意的是,把 requires_grad 设置成 true 或者 false 要灵活处理。如果是训练过程就要设置为 true,目的是方便求导、更新参数。而到了验证或者测试过程,我们的目的是检查当前模型的泛化能力,那就要把 requires_grad 设置成 Fasle,避免这个参数根据 loss 自动更新。
2.从 NumPy 中创建
还记得之前的课程中,我们一同学习了 NumPy 的使用,在实际应用中,我们在处理数据的阶段多使用的是 NumPy,而数据处理好之后想要传入 PyTorch 的深度学习模型中,则需要借助 Tensor,所以 PyTorch 提供了一个从 NumPy 转到 Tensor 的语句:
torch.from_numpy(ndarry)
创建特殊形式的 Tensor
创建零矩阵 Tensor:零矩阵顾名思义,就是所有的元素都为 0 的矩阵。
torch.zeros(*size, dtype=None...)
创建单位矩阵 Tensor:单位矩阵是指主对角线上的元素都为 1 的矩阵。
torch.eye(size, dtype=None...)
创建全一矩阵 Tensor:全一矩阵顾名思义,就是所有的元素都为 1 的矩阵。
torch.ones(size, dtype=None...)
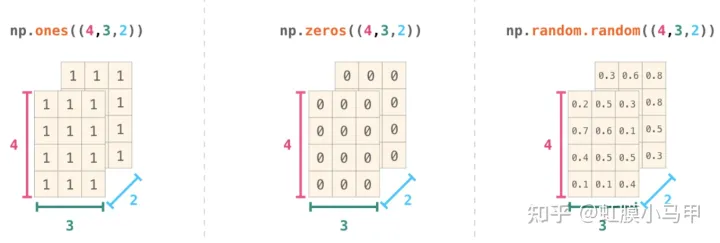
创建随机矩阵 Tensor:在 PyTorch 中有几种较为经常使用的随机矩阵创建方式,分别如下。
torch.rand(size)
torch.randn(size)
torch.normal(mean, std, size)
torch.randint(low, high, size)
这些方式各自有不同的用法,你可以根据自己的需要灵活使用。
- torch.rand 用于生成数据类型为浮点型且维度指定的随机 Tensor,随机生成的浮点数据在 0~1 区间均匀分布。
- torch.randn 用于生成数据类型为浮点型且维度指定的随机 Tensor,随机生成的浮点数的取值满足均值为 0、方差为 1 的标准正态分布。
- torch.normal 用于生成数据类型为浮点型且维度指定的随机 Tensor,可以指定均值和标准差。
- torch.randint 用于生成随机整数的 Tensor,其内部填充的是在[low,high) 均匀生成的随机整数。
Tensor 的转换
在实际项目中,我们接触到的数据类型有很多,比如 Int、list、NumPy 等。为了让数据在各个阶段畅通无阻,不同数据类型与 Tensor 之间的转换就非常重要了。接下来我们一起来看看 int、list、NumPy 是如何与 Tensor 互相转换的。
- Int 与 Tensor 的转换
a = torch.tensor(1)
b = a.item()
我们通过 torch.Tensor 将一个数字(或者标量)转换为 Tensor,又通过item()函数,将 Tensor 转换为数字(标量),item() 函数的作用就是将 Tensor 转换为一个 python number。
- list 与 tensor 的转换:
a = [1, 2, 3]
b = torch.tensor(a)
c = b.numpy().tolist()
在这里对于一个 list a,我们仍旧直接使用 torch.Tensor,就可以将其转换为 Tensor 了。而还原回来的过程要多一步,需要我们先将 Tensor 转为 NumPy 结构,之后再使用 tolist() 函数得到 list。
- NumPy 与 Tensor 的转换:
我们仍旧 torch.Tensor 即可
- CPU 与 GPU 的 Tensor 之间的转换:
CPU->GPU: data.cuda()
GPU->CPU: data.cpu()
Tensor 的常用操作
- 获取形状
在深度学习网络的设计中,我们需要时刻对 Tensor 的情况做到了如指掌,其中就包括获取 Tensor 的形式、形状等。
为了得到 Tensor 的形状,我们可以使用 shape 或 size 来获取。两者的不同之处在于,shape 是 torch.tensor 的一个属性,而 size() 则是一个 torch.tensor 拥有的方法。
>>> a=torch.zeros(2, 3, 5)
>>> a.shape
torch.Size([2, 3, 5])
>>> a.size()
torch.Size([2, 3, 5])
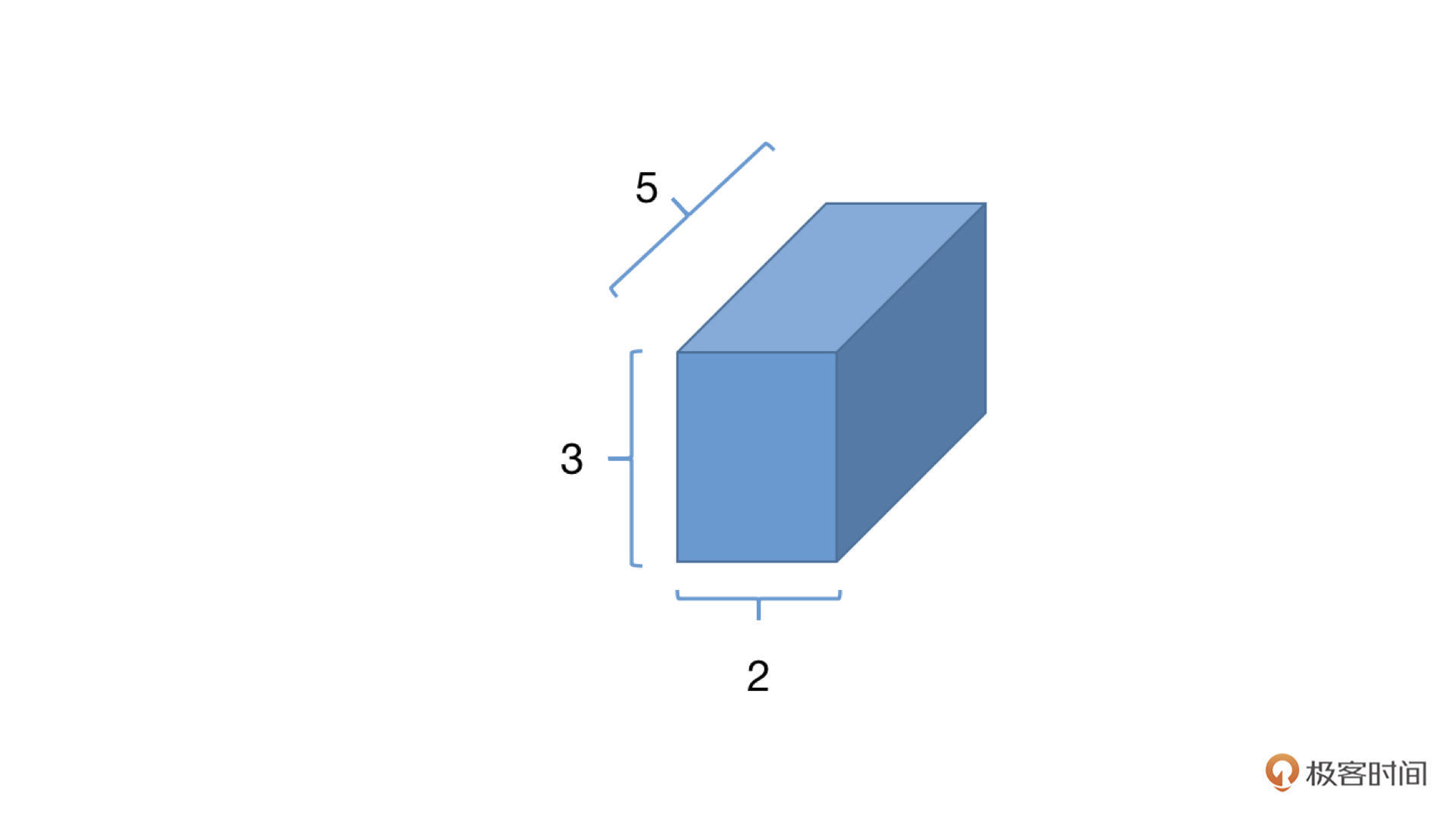
获取元素数目
>>> a.numel()
30
- 矩阵转秩 (维度转换)
在 PyTorch 中有两个函数,分别是 permute() 和 transpose() 可以用来实现矩阵的转秩,或者说交换不同维度的数据。比如在调整卷积层的尺寸、修改 channel 的顺序、变换全连接层的大小的时候,我们就要用到它们。
其中,用 permute 函数可以对任意高维矩阵进行转置,但只有 tensor.permute() 这个调用方式,我们先看一下代码:
>>> x = torch.rand(2,3,5)
>>> x.shape
torch.Size([2, 3, 5])
>>> x = x.permute(2,1,0)
>>> x.shape
torch.Size([5, 3, 2])
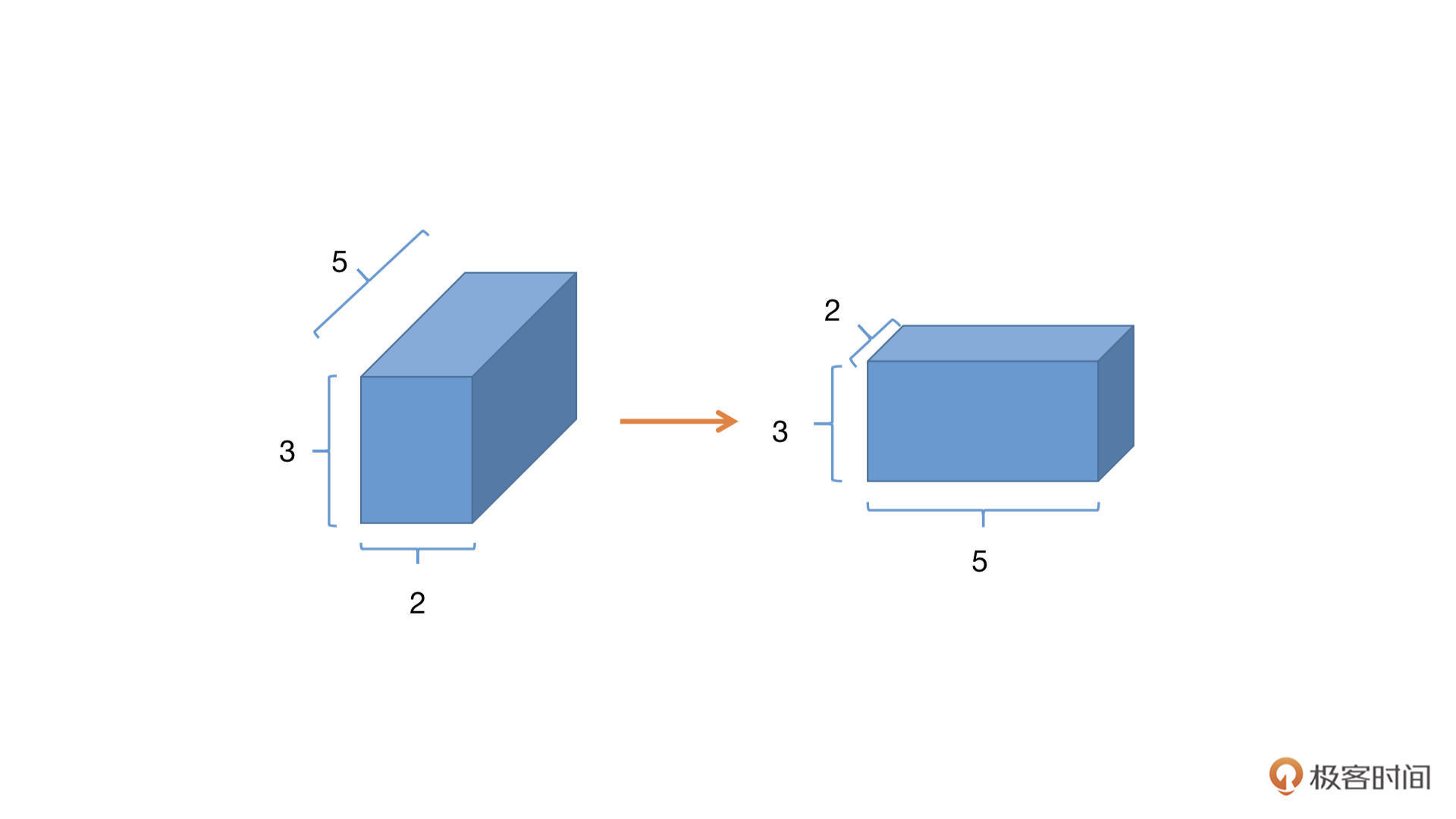
原来的 Tensor 的形状是[2,3,5],我们在 permute 中分别写入原来索引位置的新位置,x.permute(2,1,0),2 表示原来第二个维度现在放在了第零个维度;同理 1 表示原来第一个维度仍旧在第一个维度;0 表示原来第 0 个维度放在了现在的第 2 个维度,形状就变成了[5,3,2]
而另外一个函数 transpose,不同于 permute,它每次只能转换两个维度,或者说交换两个维度的数据。
>>> x.shape
torch.Size([2, 3, 4])
>>> x = x.transpose(1,0)
>>> x.shape
torch.Size([3, 2, 4])
需要注意的是,经过了 transpose 或者 permute 处理之后的数据,变得不再连续了,什么意思呢?
但一个新建的tensor,一定是连续的,行相邻的两个元素,在内存中也一定相邻。但是如果经过transpose或者permute等操作,行相邻的两个元素,在内存上不相邻了,此为不连续。注意transpose和permute并不会改变tensor的底层的一维数组,只是会改变元信息。
那么如何让经过了transpose或者permute的tensor重新变成连续?就是调用contiguous方法,它会重新生成一个tensor,新tensor底层的一维数组和原来的不一样,它是将当前tensor按行展开进行保存的。
举个例子,下面的is_contiguous()是判断tensor是否连续,data_ptr是返回tensor的数据指针
In [100]: a=torch.Tensor([[1,2,3],[4,5,6]])
In [101]: a
Out[101]:
tensor([[1., 2., 3.],
[4., 5., 6.]])
In [102]: a.is_contiguous()
Out[102]: True
# 注意:这里flatten()只是演示a在底层的一维数组的样子
# flatten的结果可不一定是底层一维数组的样子,只有在tensor连续时才刚好一样。
In [103]: a.flatten()
Out[103]: tensor([1., 2., 3., 4., 5., 6.])
# 转置后不连续了
In [104]: a.transpose(0,1).is_contiguous()
Out[104]: False
# contiguous一下又变连续了
In [107]: a.transpose(0,1).contiguous().is_contiguous()
Out[107]: True
# transpose后,还是用的同一份底层数组,
# 但是contiguous是换了一份底层数组,可以说是完全不一样的tensor
In [108]: a.data_ptr()
Out[108]: 66883392
In [109]: a.transpose(0,1).data_ptr()
Out[109]: 66883392
In [110]: a.transpose(0,1).contiguous().data_ptr()
Out[110]: 66774976
形状变换
在 PyTorch 中有两种常用的改变形状的函数,分别是view 和 reshape。我们先来看一下 view。
>>> x = torch.randn(4, 4)
>>> x.shape
torch.Size([4, 4])
>>> x = x.view(2,8)
>>> x.shape
torch.Size([2, 8])
>>> x = x.permute(1,0)
>>> x.shape
torch.Size([8, 2])
>>> x.view(4, 4)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
RuntimeError: view size is not compatible with input tensor's size and stride (at least one dimension spans across two contiguous subspaces). Use .reshape(...) instead.
结合代码可以看到,利用 permute,我们将第 0 和第 1 维度的数据进行了变换,得到了[8, 2]形状的 Tensor,在这个新 Tensor 上进行 view 操作,忽然就报错了,为什么呢?其实就是因为 view 不能处理内存不连续 Tensor 的结构。
这个时候我们要使用reshape:这样问题就迎刃而解了。其实 reshape 相当于进行了两步操作,先把 Tensor 在内存中捋顺了,然后再进行 view 操作。
>>> x = x.reshape(4, 4)
>>> x.shape
torch.Size([4, 4])
增减维度
PyTorch 提供了 squeeze() 和 unsqueeze() 函数解决这个问题。
>>> x = torch.rand(2,1,3)
>>> x.shape
torch.Size([2, 1, 3])
>>> y = x.squeeze(1)
>>> y.shape
torch.Size([2, 3])
>>> z = y.squeeze(1)
>>> z.shape
torch.Size([2, 3])
squeeze本身是清除所有维度为1的,但是你加入指定后会清楚特定位置为1的,如果不唯一就不行。
unsqueeze():这个函数主要是对数据维度进行扩充。给指定位置加上维数为 1 的维度,我们同样结合代码例子来看看。
>>> x = torch.rand(2,1,3)
>>> y = x.unsqueeze(2)
>>> y.shape
torch.Size([2, 1, 1, 3])
Tensor变形 切分
Tensor 的连接操作
- cat
cat 是 concatnate 的意思,也就是拼接、联系的意思。该函数有两个重要的参数需要你掌握。第一个参数是 tensors,它很好理解,就是若干个我们准备进行拼接的 Tensor。第二个参数是 dim。
torch.cat(tensors, dim = 0, out = None)
>>> A=torch.ones(3,3)
>>> B=2*torch.ones(3,3)
>>> A
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
>>> B
tensor([[2., 2., 2.],
[2., 2., 2.],
[2., 2., 2.]])
# axis=0
>>> C=torch.cat((A,B),0)
>>> C
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.],
[2., 2., 2.],
[2., 2., 2.],
[2., 2., 2.]])
# dim=1
>>> D=torch.cat((A,B),1)
>>> D
tensor([[1., 1., 1., 2., 2., 2.],
[1., 1., 1., 2., 2., 2.],
[1., 1., 1., 2., 2., 2.]])
cat 实际上是将多个 Tensor 在已有的维度上进行连接,那如果想增加新的维度进行连接,又该怎么做呢?这时候就需要 stack 函数登场了。
stack
为了让你加深理解,我们还是结合具体例子来看看。假设我们有两个二维矩阵 Tensor,把它们“堆叠”放在一起,构成一个三维的 Tensor,如下图:
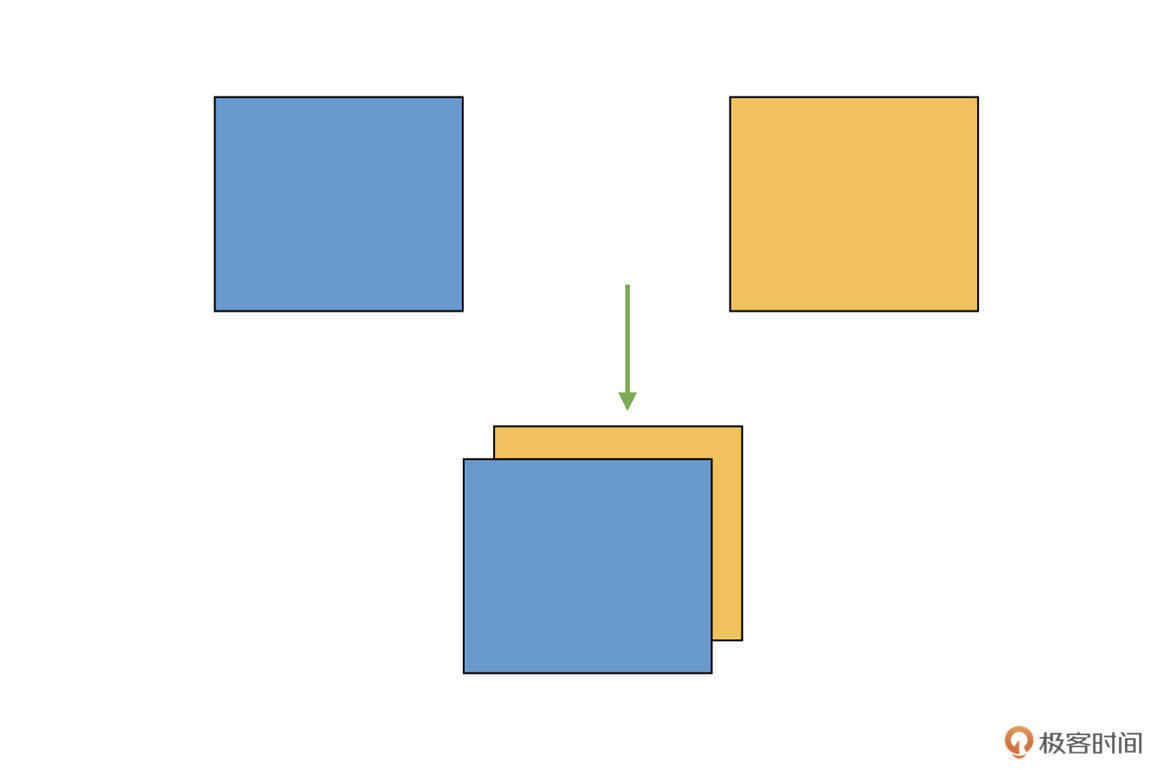
这相当于原来的维度(秩)是 2,现在变成了 3,变成了一个立体的结构,增加了一个维度。你需要注意的是,这跟前面的 cat 不同,cat 中示意图的例子,原来就是 3 维的,cat 之后仍旧是 3 维的,而现在咱们是从 2 维变成了 3 维。
在实际图像算法开发中,咱们有时候需要将多个单通道 Tensor(2 维)合并,得到多通道的结果(3 维)。而实现这种增加维度拼接的方法,我们把它叫做 stack。
其中,inputs 表示需要拼接的 Tensor,dim 表示新建立维度的方向
torch.stack(inputs, dim=0)
>>> A=torch.arange(0,4)
>>> A
tensor([0, 1, 2, 3])
>>> B=torch.arange(5,9)
>>> B
tensor([5, 6, 7, 8])
>>> C=torch.stack((A,B),0)
>>> C
tensor([[0, 1, 2, 3],
[5, 6, 7, 8]])
>>> D=torch.stack((A,B),1)
>>> D
tensor([[0, 5],
[1, 6],
[2, 7],
[3, 8]])
E=torch.stack((C,C),0)
print(E)
tensor([[[0, 1, 2, 3],
[5, 6, 7, 8]],
[[0, 1, 2, 3],
[5, 6, 7, 8]]])
结合代码,我们可以看到,首先我们构建了两个 4 元素向量 A 和 B,它们的维度是 1。然后,我们在 dim=0,也就是“行”的方向上新建一个维度,这样维度就成了 2,也就得到了 C。而对于 D,我们则是在 dim=1,也就是“列”的方向上新建维度。
Tensor 的切分操作
切分就是连接的逆过程,有了刚才的经验,你很容易就会想到,切分的操作也应该有很多种,比如切片、切块等。没错,切分的操作主要分为三种类型:chunk、split、unbind。
chunk
chunk 的作用就是将 Tensor 按照声明的 dim,进行尽可能平均的划分。
torch.chunk(input, chunks, dim=0)
首先是 input,它表示要做 chunk 操作的 Tensor。接着,我们看下 chunks,它代表将要被划分的块的数量,而不是每组的数量。请注意,chunks 必须是整型。最后是 dim,就是按照哪个维度来进行 chunk。
比如说,我们有一个 32channel 的特征,需要将其按照 channel 均匀分成 4 组,每组 8 个 channel,这个切分就可以通过 chunk 函数来实现。具体函数如下:
>>> A=torch.tensor([1,2,3,4,5,6,7,8,9,10])
>>> B = torch.chunk(A, 2, 0)
>>> B
(tensor([1, 2, 3, 4, 5]), tensor([ 6, 7, 8, 9, 10]))
当元素不够时,其实在计算每个结果元素个数的时候,chunk 函数是先做除法,然后再向上取整得到每组的数量。
二维
>>> A=torch.ones(4,4)
>>> A
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
>>> B = torch.chunk(A, 2, 0)
>>> B
(tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.]]),
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.]]))
Split
那如果想按照“每份按照确定的大小”来进行切分,PyTorch 也提供了相应的方法,叫做 split。
torch.split(tensor, split_size_or_sections, dim=0)
# 首先是 tensor,也就是待切分的 Tensor。然后是 split_size_or_sections 这个参数。当它为整数时,表示将 tensor 按照每块大小为这个整数的数值来切割;当这个参数为列表时,则表示将此 tensor 切成和列表中元素一样大小的块。最后同样是 dim,它定义了要按哪个维度切分。
>>> A=torch.rand(4,4)
>>> A
tensor([[0.6418, 0.4171, 0.7372, 0.0733],
[0.0935, 0.2372, 0.6912, 0.8677],
[0.5263, 0.4145, 0.9292, 0.5671],
[0.2284, 0.6938, 0.0956, 0.3823]])
>>> B=torch.split(A, 2, 0)
>>> B
(tensor([[0.6418, 0.4171, 0.7372, 0.0733],
[0.0935, 0.2372, 0.6912, 0.8677]]),
tensor([[0.5263, 0.4145, 0.9292, 0.5671],
[0.2284, 0.6938, 0.0956, 0.3823]]))
如果 split_size_or_sections 不能整除对应方向的大小的话,会有怎样的结果呢.PyTorch 会尽可能凑够每一个结果,使得其对应 dim 的数据大小等于 split_size_or_sections。如果最后剩下的不够,那就把剩下的内容放到一块,作为最后一个结果。
接下来,我们再看一下 split_size_or_sections 是列表时的情况。刚才提到了,当 split_size_or_sections 为列表的时候,表示将此 tensor 切成和列表中元素大小一样的大小的块,我们来看一段对应的代码
这部分代码怎么解释呢?其实也很好理解,就是将 Tensor A,沿着第 0 维进行切分,每一个结果对应维度上的尺寸或者说大小,分别是 2(行),3(行)。
>>> A=torch.rand(5,4)
>>> A
tensor([[0.1005, 0.9666, 0.5322, 0.6775],
[0.4990, 0.8725, 0.5627, 0.8360],
[0.3427, 0.9351, 0.7291, 0.7306],
[0.7939, 0.3007, 0.7258, 0.9482],
[0.7249, 0.7534, 0.0027, 0.7793]])
>>> B=torch.split(A,(2,3),0)
>>> B
(tensor([[0.1005, 0.9666, 0.5322, 0.6775],
[0.4990, 0.8725, 0.5627, 0.8360]]),
tensor([[0.3427, 0.9351, 0.7291, 0.7306],
[0.7939, 0.3007, 0.7258, 0.9482],
[0.7249, 0.7534, 0.0027, 0.7793]]))
unbind
通过学习前面的几个函数,咱们知道了怎么按固定大小做切分,或者按照索引 index 来进行选择。现在我们想象一个应用场景,如果我们现在有一个 3 channel 图像的 Tensor,想要逐个获取每个 channel 的数据,该怎么做呢?
假如用 chunk 的话,我们需要将 chunks 设为 3;如果用 split 的话,需要将 split_size_or_sections 设为 1。虽然它们都可以实现相同的目的,但是如果 channel 数量很大,逐个去取也比较折腾。这时候,就需要用到另一个函数:unbind,它的函数定义如下:
>>> A=torch.arange(0,16).view(4,4)
>>> A
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
>>> b=torch.unbind(A, 0)
>>> b
(tensor([0, 1, 2, 3]),
tensor([4, 5, 6, 7]),
tensor([ 8, 9, 10, 11]),
tensor([12, 13, 14, 15]))
接下来,我们看一下:如果从第 1 维,也就是“列”的方向进行切分,会是怎样的结果呢:
>>> b=torch.unbind(A, 1)
>>> b
(tensor([ 0, 4, 8, 12]),
tensor([ 1, 5, 9, 13]),
tensor([ 2, 6, 10, 14]),
tensor([ 3, 7, 11, 15]))
不难发现,这里是按照“列”的方向进行拆解的。所以,unbind 是一种降维切分的方式,相当于删除一个维度之后的结果。
Tensor 的索引操作
你有没有发现,刚才我们讲的 chunk 和 split 操作,我们都是将数据整体进行切分,并获得全部结果。但有的时候,我们只需要其中的一部分,这要怎么做呢?
一个很自然的想法就是,直接告诉 Tensor 我想要哪些部分,这种方法我们称为索引操作。索引操作有很多方式,有提供好现成 API 的,也有用户自行定制的操作,其中最常用的两个操作就是 index_select 和 masked_select,我们分别去看看用法。
index_select
我们重点看一看 index,它表示从 dim 维度中的哪些位置选择数据,这里需要注意,index是 torch.Tensor 类型。
torch.index_select(tensor, dim, index)
>>> A=torch.arange(0,16).view(4,4)
>>> A
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
>>> B=torch.index_select(A,0,torch.tensor([1,3]))
>>> B
tensor([[ 4, 5, 6, 7],
[12, 13, 14, 15]])
>>> C=torch.index_select(A,1,torch.tensor([0,3]))
>>> C
tensor([[ 0, 3],
[ 4, 7],
[ 8, 11],
[12, 15]])
在这个例子中,我们先创建了一个 4x4 大小的矩阵 Tensor A。然后,我们从第 0 维选择第 1(行)和 3(行)的数据,并得到了最终的 Tensor B,其大小为 2x4。随后我们从 Tensor A 中选择第 0(列)和 3(列)的数据,得到了最终的 Tensor C,其大小为 4x2。
masked_select
刚才介绍的 indexed_select,它是基于给定的索引来进行数据提取的。
但有的时候,我们还想通过一些判断条件来进行选择,比如提取深度学习网络中某一层中数值大于 0 的参数。这时候,就需要用到 PyTorch 提供的 masked_select 函数了,我们先来看它的定义:
torch.masked_select(input, mask, out=None)
input 表示待处理的 Tensor。mask 代表掩码张量,也就是满足条件的特征掩码。这里你需要注意的是,mask 须跟 input 张量有相同数量的元素数目,但形状或维度不需要相同。
Eg:
你在平时的练习中有没有想过,如果我们让 Tensor 和数字做比较,会有什么样的结果?比如后面这段代码,我们随机生成一个 5 位长度的 Tensor A:
>>> A=torch.rand(5)
>>> A
tensor([0.3731, 0.4826, 0.3579, 0.4215, 0.2285])
>>> B=A>0.3
>>> B
tensor([ True, True, True, True, False])
这个新的 Tensor 其实就是一个掩码张量,它的每一位表示了一个判断条件是否成立的结果。
然后,我们继续写一段代码,看看基于掩码 B 的选择是怎样的结果 :
>>> C=torch.masked_select(A, B)
>>> C
tensor([0.3731, 0.4826, 0.3579, 0.4215])
你会发现,C 实际上得到的就是:A 中“满足 B 里面元素值为 True 的”对应位置的数据。
>>> A=torch.rand(5)
>>> A
tensor([0.3731, 0.4826, 0.3579, 0.4215, 0.2285])
>>> C=torch.masked_select(A, A>0.3)
>>> C
tensor([0.3731, 0.4826, 0.3579, 0.4215])
pandas
数据结构
Series 是一种类似于一维数组的对象,它由一组数据(各种Numpy数据类型)以及一组与之相关的数据标签(即索引)组成。
DataFrame 是一个表格型的数据结构,它含有一组有序的列,每列可以是不同的值类型(数值、字符串、布尔型值)。DataFrame 既有行索引也有列索引,它可以被看做由 Series 组成的字典(共同用一个索引)。
DataFrame
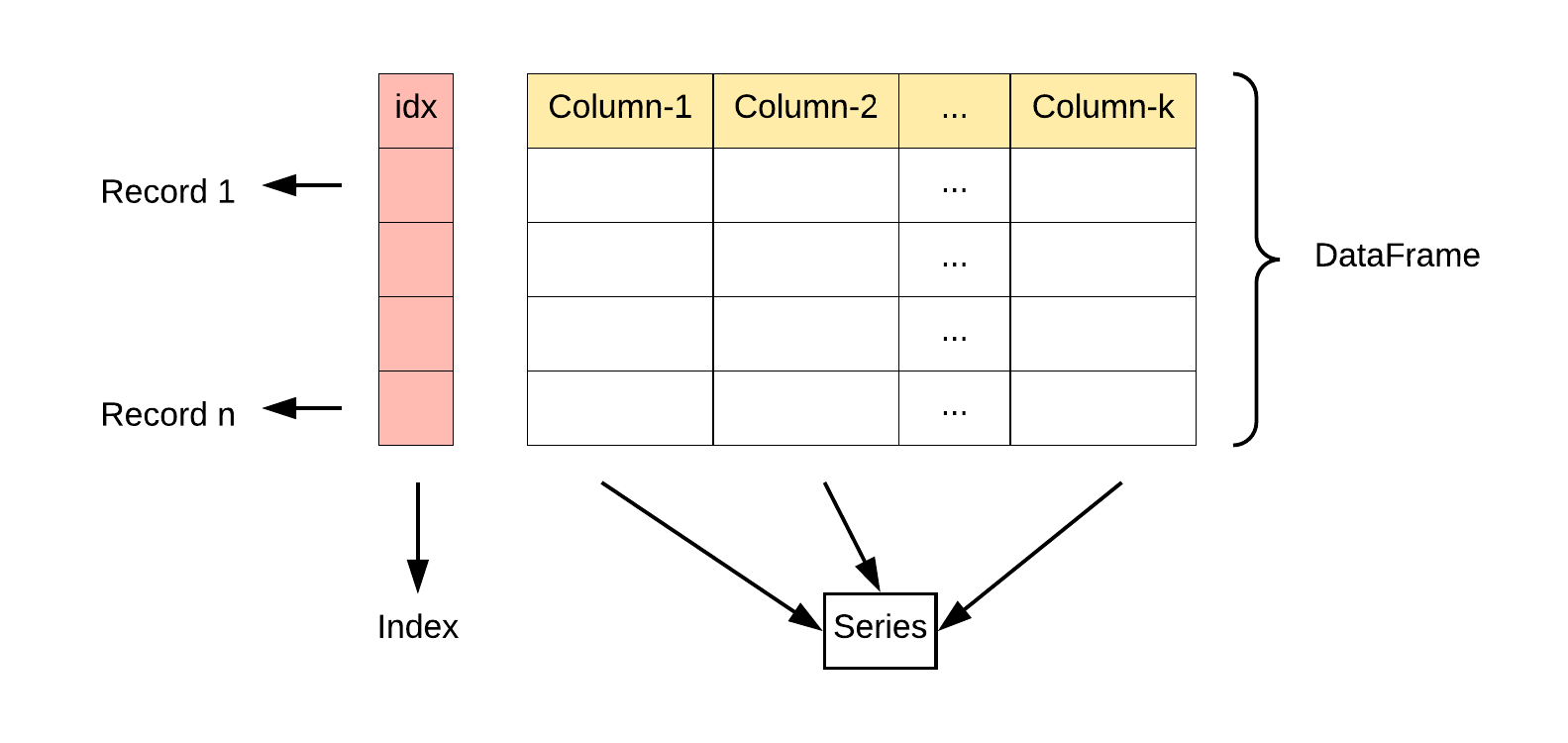

DataFrame 构造方法如下:
pandas.DataFrame( data, index, columns, dtype, copy)
参数说明:
- data:一组数据(ndarray、series, map, lists, dict 等类型)。
- index:索引值,或者可以称为行标签。
- columns:列标签,默认为 RangeIndex (0, 1, 2, …, n) 。
- dtype:数据类型。
- copy:拷贝数据,默认为 False。
Pandas 可以使用 loc 属性返回指定行的数据,如果没有设置索引,第一行索引为 0,第二行索引为 1
具体参考官网:https://www.runoob.com/pandas/pandas-dataframe.html
import pandas as pd
data = {
"calories": [420, 380, 390],
"duration": [50, 40, 45]
}
df = pd.DataFrame(data, index = ["day1", "day2", "day3"])
print(df)
calories duration
day1 420 50
day2 380 40
day3 390 45
CSV
我们也可以使用 to_csv() 方法将 DataFrame 存储为 csv 文件:
**Pandas Series **
类似表格中的一个列(column),类似于一维数组,可以保存任何数据类型。
Series 由索引(index)和列组成,函数如下:
pandas.Series( data, index, dtype, name, copy)
官网:https://www.runoob.com/pandas/pandas-series.html
import pandas as pd
sites = {1: "Google", 2: "Runoob", 3: "Wiki"}
myvar = pd.Series(sites, index = [1, 2])
print(myvar)
1 google
2 runoob
matplotlib
看官网demo即可https://matplotlib.org/stable/gallery/index.html





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本