树形结构

二叉树

二叉树是由节点点组成的，每一个结点包含父节点的地址值和左右子节点的地址值以及自己的属性值，如下图所示：

 

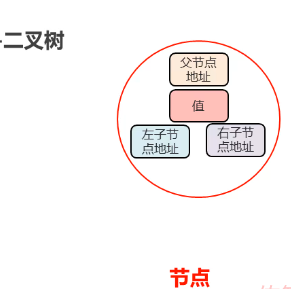
 二叉树的定义：每一个结点最多有不超过两个的子节点，可以没有子节点

 

 

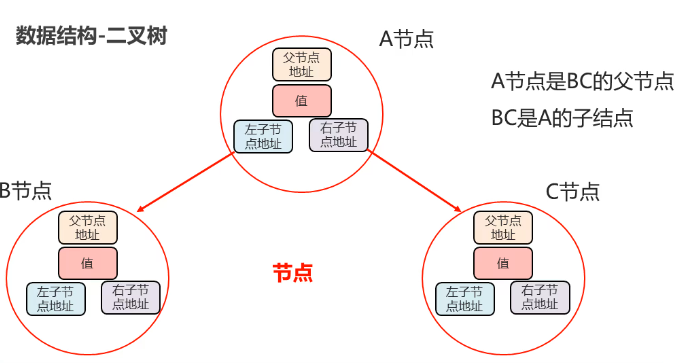
二叉树实例：

 

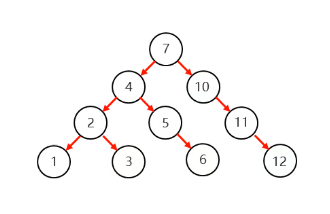
 （二叉树相对简单不做过多描述）

二叉查找树

二叉查找树首先要是一棵二叉树，二叉查找树的结构特点是每一个节点的左子节点都小于父节点，每一个节点的有子节点都大于父节点，例如：

 

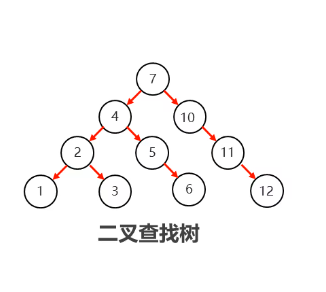
 二叉查找树的口诀是左小右大，添加的时候可以按照此口诀进行添加，二叉查找树也相对简单，不做过多描述。

平衡二叉树

• 二叉树的左右两棵子树的高度差不差过1,
• 热任意每个结点的左右子树都是可二叉树

例如：

 

 

 左旋和右旋

为了提高二叉查找树的查找效率，我们要将不平衡的二叉查找树变成一棵平衡二叉查找树，这就涉及的左旋和右旋

左旋（右右）

下面有一棵不平衡的二叉查找树：

 

 右子树的高度比左子树的高度大二，此时要左旋，将10变成根节点

 

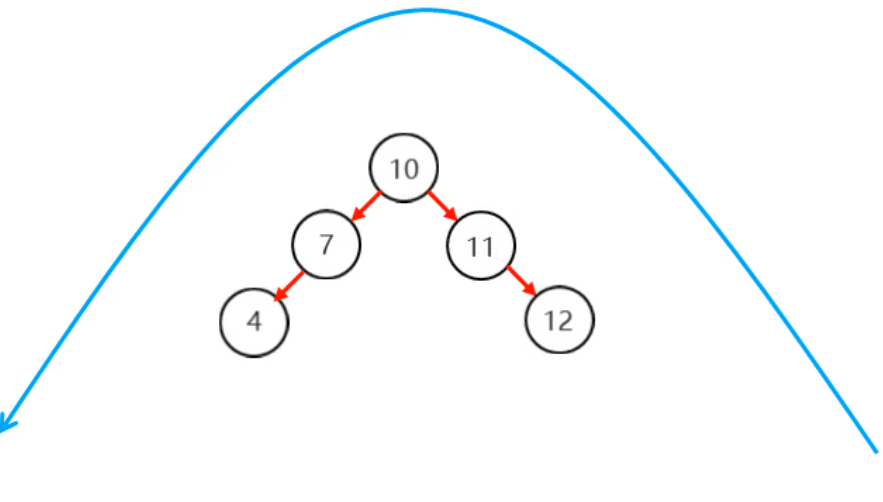
 看下面这种情况的左旋：

 

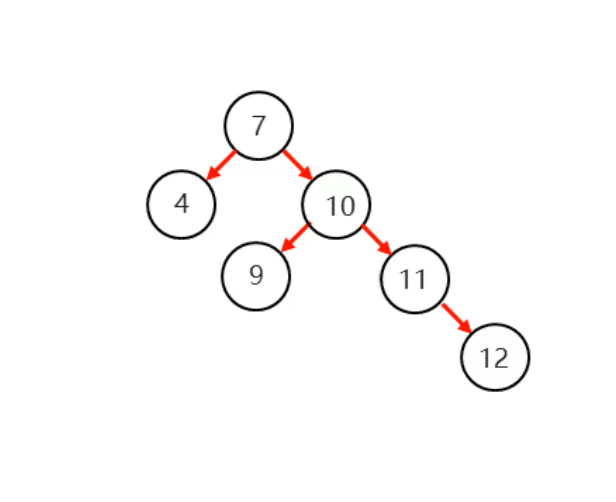
 左旋之后

 

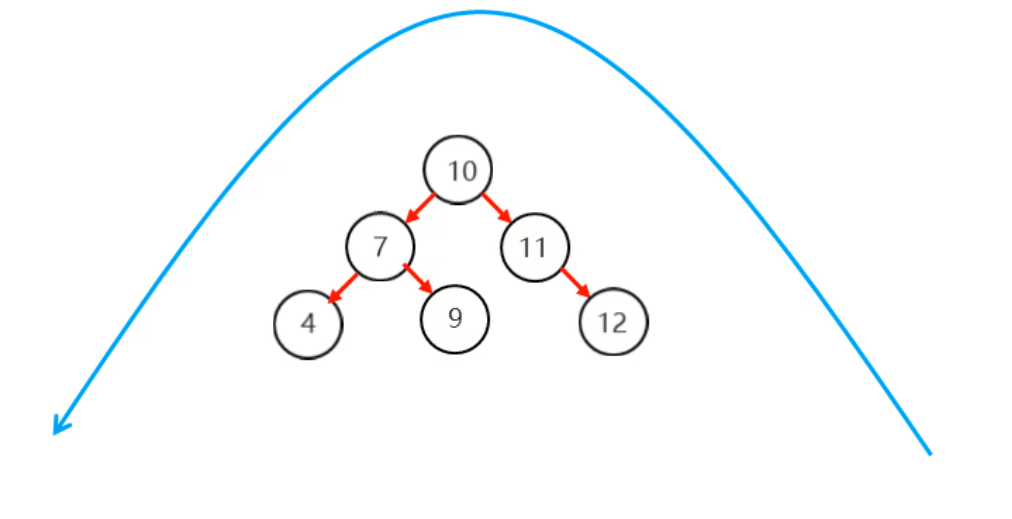
原来10结点的左子结点是9，左旋之后10的左子节点是7，而原来的左子节点9变成了现在左子节点的右子节点。（口诀是旧爱不及新欢，新欢怜旧爱） 

左旋（右左）

 

 

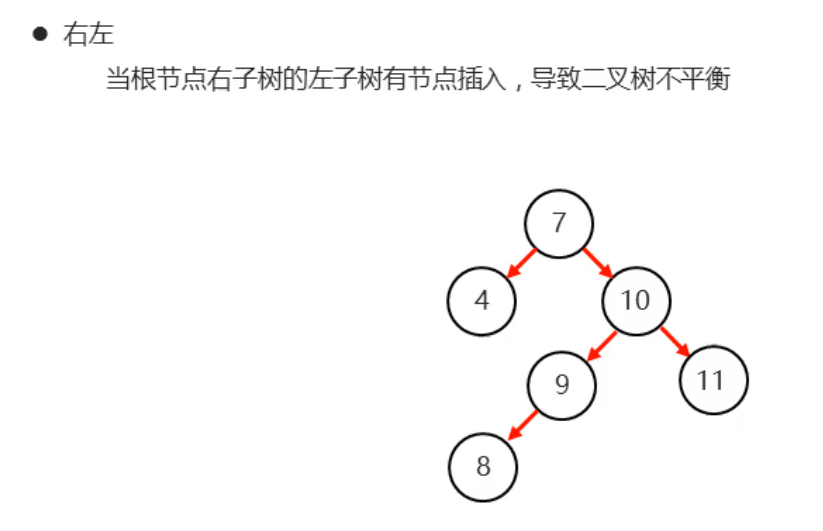
方法：

• 先将柚子树右旋
• 然后整体左旋

第一步：

 

 

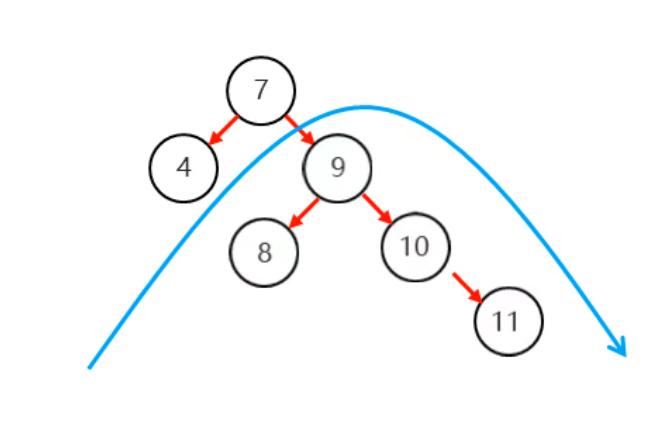
第二步：

 

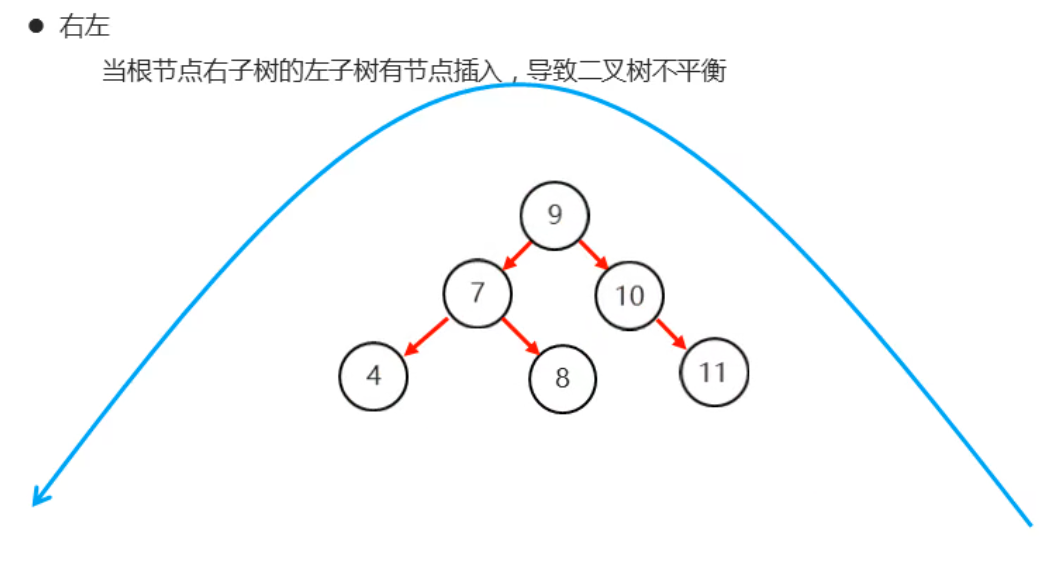
 总结：右左右旋变右右，右右左旋变平衡。

类似的，左右：左右左旋变左左，左左右旋变平衡

 

 

红黑树

简介：

 

 

 红黑规则：

 

 

红黑规则口诀：

根叶都是黑，

红色不相连，

到叶黑相等。

 

红黑树添加元素的默认元素我们规定为红色（默认为红色的添加效率更高）

添加规则概述：

 

 

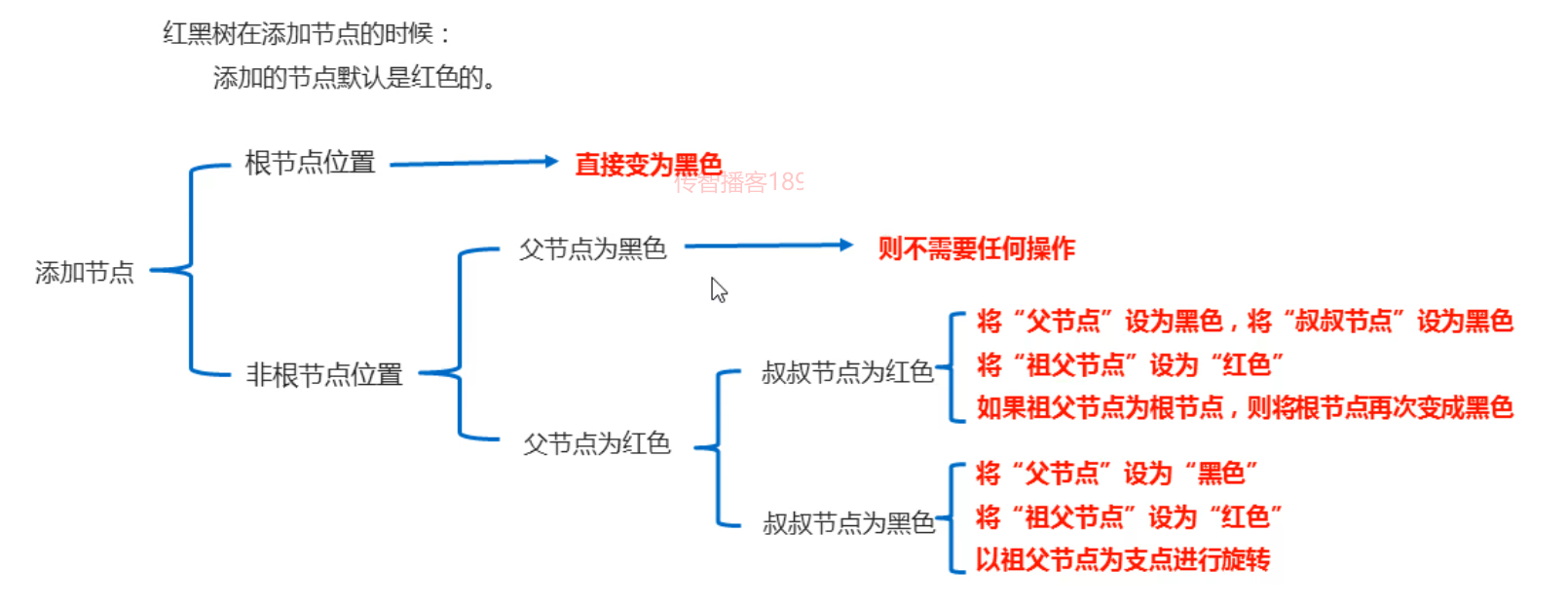
我们从添加父节点为红色讲起，也就是上图中的地三步的父节点为红色：

这样就分两种情况：

• 叔叔节点为红色
• 叔叔节点为黑色

叔叔结点为红色则将父节点和叔节点都变成黑色，祖父结点变成红色，如果祖父结点为根节点，则祖父结点再变成黑色。图解如下：

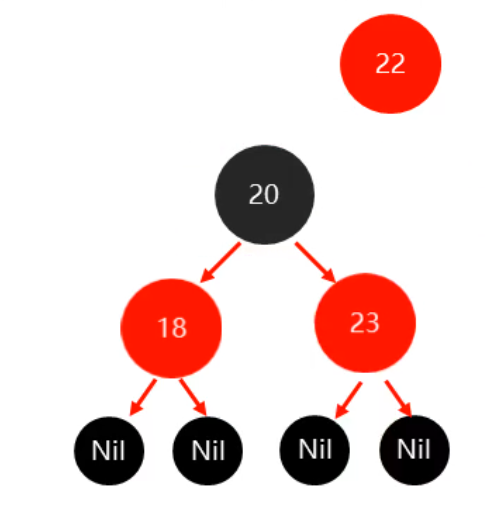
插入22之后：

 

 

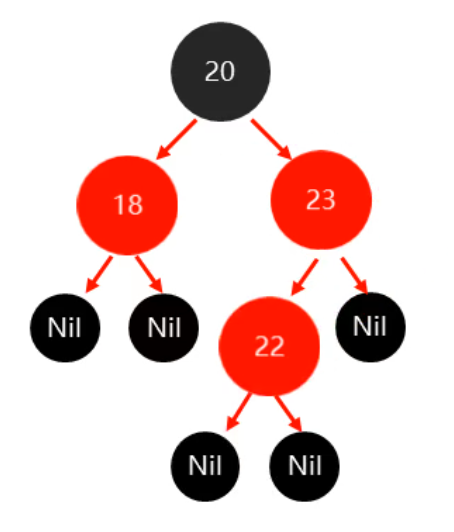
 此时不满足红色不相连的规则，其父叔的颜色都是红色，则把父叔都变黑，祖父变红。

 

 

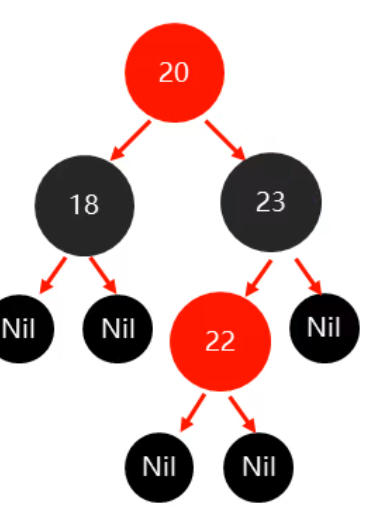
祖父为根节点再变红：

 

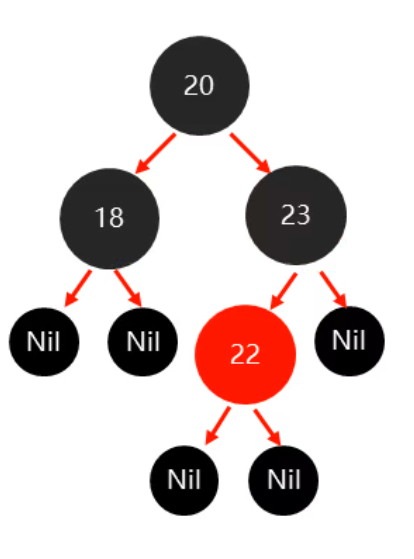
 叔节点为黑色则将父节点变成黑色，祖父结点变成红色，然后以祖父结点为支点进行旋转，图解如下：

 

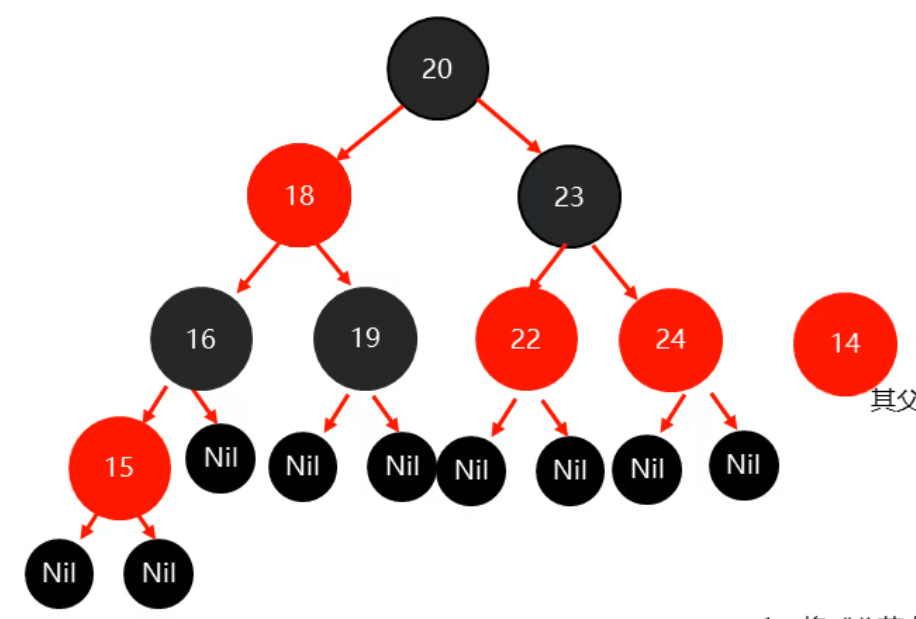
 14节点添加之后为：

 

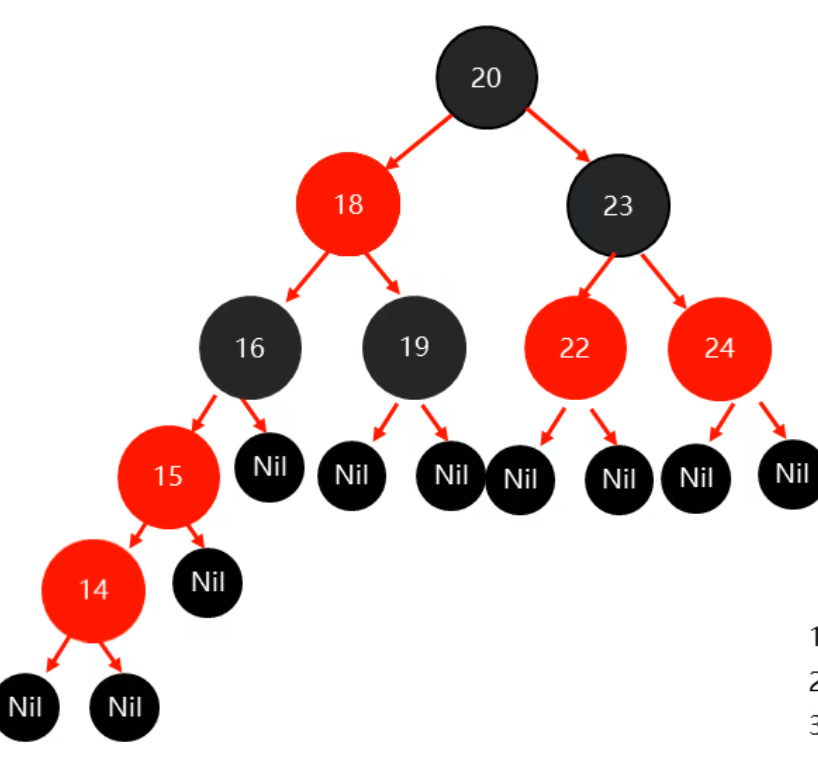
 将父节点变成黑色，将祖父结点变成红色：

 

 

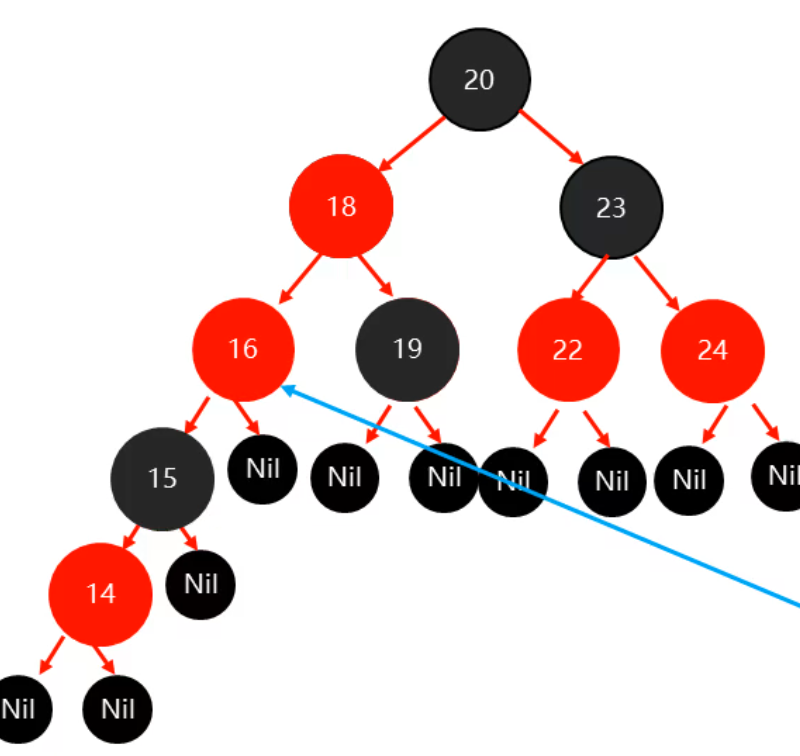
以祖父结点为支点进行旋转：

 

 

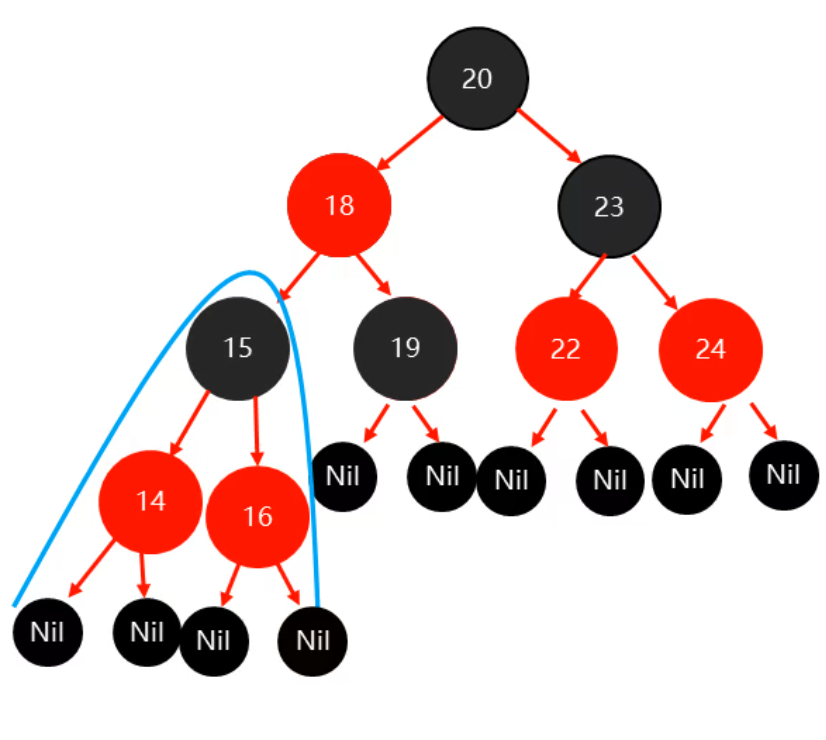
树形结构到此结束。