2024-2025-1 20241307《计算机基础与程序设计》第七周学习总结

作业信息

这个作业属于哪个课程 （2024-2025-1-计算机基础与程序设计）
这个作业要求在哪里 (2024-2025-1计算机基础与程序设计第七周作业)
这个作业的目标
作业正文 （2024-2025-1 学号20241307《计算机基础与程序设计》第七周学习总结）

教材学习内容总结

《计算机科学概论（第七版）第 8 章总结》

一、抽象数据类型

  1. 数据结构概述
    • 数据结构是组织和存储数据的方式，以便于高效地访问和修改数据。不同的数据结构适用于不同的应用场景，它们在数据的插入、删除、检索等操作上具有不同的时间和空间复杂度。
    • 例如，数组是一种简单的数据结构，它在内存中连续存储元素，通过下标可以快速访问元素，但插入和删除操作可能比较耗时，因为需要移动大量元素。而链表则不同，它的元素在内存中不连续存储，每个元素包含指向下一个元素的指针，插入和删除操作相对灵活，但访问特定元素需要遍历链表，时间复杂度较高。
  2. 栈（Stack）
    • 栈是一种特殊的数据结构，遵循后进先出（LIFO - Last In First Out）原则。就像一摞盘子，最后放上去的盘子最先被拿走。
    • 在计算机中，栈常用于函数调用过程。当一个函数被调用时，其返回地址、局部变量等信息会被压入栈中，函数执行完毕后，这些信息再从栈中弹出，以便程序继续执行调用函数之前的代码。例如，在递归函数中，每一次递归调用都会将当前函数的状态信息压入栈，直到达到递归终止条件，然后再依次从栈中弹出信息，返回结果。
    • 栈的基本操作包括入栈（Push），即将一个元素添加到栈顶；出栈（Pop），即移除栈顶元素并返回其值；以及查看栈顶元素（Peek）等。
  3. 队列（Queue）
    • 队列是先进先出（FIFO - First In First Out）的数据结构，类似于排队等候服务的人群，先到的人先接受服务。
    • 它在计算机系统中有很多应用，比如操作系统中的任务调度。当多个任务等待 CPU 处理时，它们可以按照到达的顺序排成队列，CPU 按照队列顺序依次处理任务。
    • 队列的主要操作有入队（Enqueue），将元素添加到队列末尾；出队（Dequeue），移除队列头部的元素并返回其值。
  4. 列表（List）
    • 列表是一种有序的元素集合，可以包含不同类型的元素。它提供了灵活的操作，如在任意位置插入和删除元素。
    • 例如，在一个图形用户界面的列表框中显示的项目就可以看作是一个列表数据结构。用户可以添加、删除或修改列表中的项目，程序可以方便地遍历列表来处理每个项目的显示、更新等操作。
    • 列表的实现方式有多种，如链表实现的列表在插入和删除元素时不需要移动大量元素，但访问元素可能相对较慢；而数组实现的列表访问元素速度快，但插入和删除操作可能涉及较多元素的移动。
  5. 树（Tree）
    • 树是一种层次化的数据结构，由节点（Node）和边（Edge）组成。有一个特殊的节点称为根节点（Root），从根节点开始，每个节点可以有零个或多个子节点。
    • 二叉树是树结构的一种特殊情况，每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树在数据检索和排序方面有广泛应用，例如二叉搜索树（Binary Search Tree），它的特点是左子树中的所有节点值都小于根节点值，右子树中的所有节点值都大于根节点值。这样在查找一个值时，可以通过比较节点值与目标值的大小，快速决定在左子树还是右子树中继续查找，大大提高了检索效率。
    • 树的遍历方式主要有前序遍历（根节点 -> 左子树 -> 右子树）、中序遍历（左子树 -> 根节点 -> 右子树）和后序遍历（左子树 -> 右子树 -> 根节点），这些遍历方式在处理树状数据结构时非常重要，比如在计算表达式树的值时，不同的遍历顺序会得到不同的结果。

二、参数传递

  1. 形参和实参的概念
    • 形参（Formal Parameter）是在函数定义时声明的参数，它只是一个占位符，用于表示函数在调用时将会接收的值。例如在函数 int add(int a, int b) 中，a 和 b 就是形参，它们在函数体内部代表将要传入的两个整数。
    • 实参（Actual Parameter）是在函数调用时实际传递给函数的具体值或变量。例如在调用 add 函数时，add(3, 5)，这里的 3 和 5 就是实参，它们分别被传递给形参 a 和 b，然后函数根据这些值进行计算并返回结果。
  2. 参数传递方式的影响
    • 值传递（Pass by Value）：在这种方式下，函数接收的是实参的值的副本。这意味着函数内部对形参的修改不会影响到实参本身。例如，定义一个函数 void increment(int x)，在函数内部将 x 加 1，但是在函数外部调用时，传递的实参变量的值不会改变。这种方式保证了数据的安全性，防止函数意外修改外部数据。
    • 引用传递（Pass by Reference）：函数接收的是实参的引用（地址）。这样函数内部对形参的操作实际上就是对实参本身的操作。例如，在 C++ 中可以使用引用类型来实现引用传递，void modify(int& x)，在函数内部对 x 的修改会直接反映到实参变量上。引用传递可以提高程序的效率，尤其是在处理大型数据结构时，避免了数据的复制开销，但需要谨慎使用，以免引起意外的副作用。

《C 语言程序设计》第 6 章总结

一、数组

  1. 一维数组
    • 定义与声明：
      • 一维数组的定义格式为 数据类型 数组名[数组大小];。例如 int arr[10]; 定义了一个名为 arr 的整型数组，它可以存储 10 个整数。数组大小必须是一个常量表达式，在编译时就确定了数组的长度。
      • 数组在内存中是连续存储的，按照下标顺序依次存放元素。例如对于 int arr[5];，arr[0] 的地址最低，arr[4] 的地址最高，且相邻元素的地址相差 sizeof(int) 字节（假设 int 类型占 4 个字节）。
    • 初始化：
      • 可以在定义数组时进行初始化，如 int arr[5] = {1, 2, 3, 4, 5};，这种方式将数组的前 5 个元素分别初始化为 1、2、3、4、5。如果初始化的值少于数组大小，未初始化的元素会被自动初始化为 0（对于全局数组和静态局部数组）或不确定值（对于自动局部数组）。
      • 也可以省略数组大小，让编译器根据初始化的值自动确定数组大小，例如 int arr[] = {1, 2, 3, 4, 5};，此时数组 arr 的大小为 5。
    • 元素访问：
      • 通过下标来访问数组元素，下标从 0 开始。例如 arr[0] 表示数组的第一个元素，arr[3] 表示数组的第四个元素。可以对数组元素进行读写操作，如 arr[2] = 10; 将数组的第三个元素赋值为 10。
  2. 二维数组
    • 定义与声明：
      • 二维数组的定义格式为 数据类型 数组名[行数][列数];。例如 int matrix[3][4]; 定义了一个 3 行 4 列的二维整型数组。二维数组可以看作是一个由多个一维数组组成的数组，每个一维数组的长度为列数。
      • 在内存中，二维数组也是按顺序存储的，先存储第一行的元素，然后是第二行，以此类推。例如对于 int matrix[2][3];，元素的存储顺序为 matrix[0][0]、matrix[0][1]、matrix[0][2]、matrix[1][0]、matrix[1][1]、matrix[1][2]。
    • 初始化：
      • 可以按行进行初始化，如 int matrix[2][3] = {{1, 2, 3}, {4, 5, 6}};，这种方式清晰地表示了每行的元素值。也可以省略行数，让编译器根据初始化的值自动确定行数，例如 int matrix[][3] = {{1, 2, 3}, {4, 5, 6}};，此时编译器根据有两组初始化值确定行数为 2。
    • 元素访问：
      • 使用两个下标来访问二维数组的元素，第一个下标表示行，第二个下标表示列。例如 matrix[1][2] 表示二维数组 matrix 中第二行第三列的元素。同样可以对二维数组元素进行读写操作，如 matrix[0][1] = 20; 将第一行第二列的元素赋值为 20。
  3. 字符数组
    • 定义与声明：
      • 字符数组用于存储字符串，定义方式与普通数组类似，如 char str[10]; 可以存储长度不超过 9 个字符的字符串（因为需要留出一个位置给字符串结束符 '\0'）。
    • 初始化：
      • 可以通过字符常量逐个初始化字符数组，如 char str[5] = {'H', 'e', 'l', 'l', 'o'};，但这种方式不会自动添加字符串结束符 '\0'。更常用的是使用字符串字面量进行初始化，如 char str[] = "Hello";，此时编译器会自动在字符串末尾添加 '\0'，并且会根据字符串的长度确定数组的大小为 6（包括 '\0'）。
    • 字符串处理函数：
      • C 语言标准库提供了许多用于字符数组（字符串）处理的函数。例如 strcpy 函数用于将一个字符串复制到另一个字符数组中，strcpy(str1, str2); 会将 str2 中的字符串复制到 str1 中，但要确保 str1 有足够的空间来存储 str2 的内容。
      • strlen 函数用于计算字符串的长度，不包括字符串结束符 '\0'。例如 int len = strlen(str); 会返回 str 字符串的实际字符个数。还有 strcat 函数用于连接两个字符串等。

二、循环结构在数组中的应用

  1. 遍历数组
    • 通常使用 for 循环来遍历一维数组。例如，要计算一维数组 int arr[10]; 中所有元素的和，可以使用以下代码：
int sum = 0;
for (int i = 0; i < 10; i++) {
    sum += arr[i];
}
  • 对于二维数组，可以使用嵌套的 for 循环来遍历。例如，要打印一个二维数组 int matrix[3][4]; 的所有元素，可以这样做：
for (int i = 0; i < 3; i++) {
    for (int j = 0; j < 4; j++) {
        printf("%d ", matrix[i][j]);
    }
    printf("\n");
}
  1. 数组元素的查找与修改
    • 可以在循环中查找数组中的特定元素。例如，要在一维数组 int arr[10]; 中查找值为 5 的元素，可以使用以下代码：
int target = 5;
int index = -1;
for (int i = 0; i < 10; i++) {
    if (arr[i] == target) {
        index = i;
        break;
    }
}
if (index!= -1) {
    printf("元素 5 在数组中的下标为 %d\n", index);
} else {
    printf("数组中未找到元素 5\n");
}
  • 同样，可以在循环中修改满足特定条件的数组元素。例如，将一维数组中所有偶数元素乘以 2：
for (int i = 0; i < 10; i++) {
    if (arr[i] % 2 == 0) {
        arr[i] *= 2;
    }
}

三、数组作为函数参数

  1. 一维数组作为函数参数
    • 当一维数组作为函数参数时，实际上传递的是数组的首地址。在函数定义中，形参可以写成数组的形式，也可以写成指针的形式。例如：
void printArray(int arr[], int size);
// 等价于
void printArray(int* arr, int size);
  • 在函数内部，可以像操作普通数组一样操作形参数组，但要注意不能在函数内部确定数组的大小（因为传递的只是地址，没有数组大小信息），所以通常需要额外传递一个表示数组大小的参数。例如：
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
  1. 二维数组作为函数参数
    • 二维数组作为函数参数时，在函数定义中必须指定二维数组的列数。例如：
void processMatrix(int matrix[][4], int rows);
  • 这是因为在内存中二维数组是按行存储的，知道列数才能正确地访问数组元素。在函数内部，可以使用嵌套的循环来处理二维数组，就像在普通的二维数组操作中一样。例如：
void processMatrix(int matrix[][4], int rows) {
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < 4; j++) {
            // 对 matrix[i][j] 进行处理
        }
    }
}

教材学习中的问题和解决过程（先问 AI）

  • 问题1：数据结构概念混淆
    问题描述：栈、队列、列表和树等数据结构的概念和操作特点容易混淆。例如，可能会错误地认为栈和队列的操作方式相同，或者不能准确理解二叉树的左右子树关系以及检索规则。
  • 问题1解决方案：通过制作表格或者思维导图来梳理栈、队列、列表和树等数据结构的定义、操作特点、应用场景等内容。例如，对于栈和队列，可以列出它们的操作（入栈 / 入队、出栈 / 出队等）以及对应的时间复杂度，通过对比来加深理解。同时，可以结合实际生活中的例子来理解数据结构，如将栈类比为一摞书（最后放上去的最先拿走），队列类比为排队买票（先来先服务）。
  • 问题2：数据结构实现细节理解困难
    问题描述：在学习数据结构的具体实现，如链表实现列表或者二叉树的节点结构时，难以理解代码中的指针操作或者节点之间的关联方式。
  • 问题2解决方案：编写简单的函数，分别使用值传递和引用传递的方式传递参数，在函数内部对形参进行操作，然后观察实参的变化情况。通过详细分析代码执行过程中的变量值和内存地址变化来理解参数传递机制。

基于AI的学习





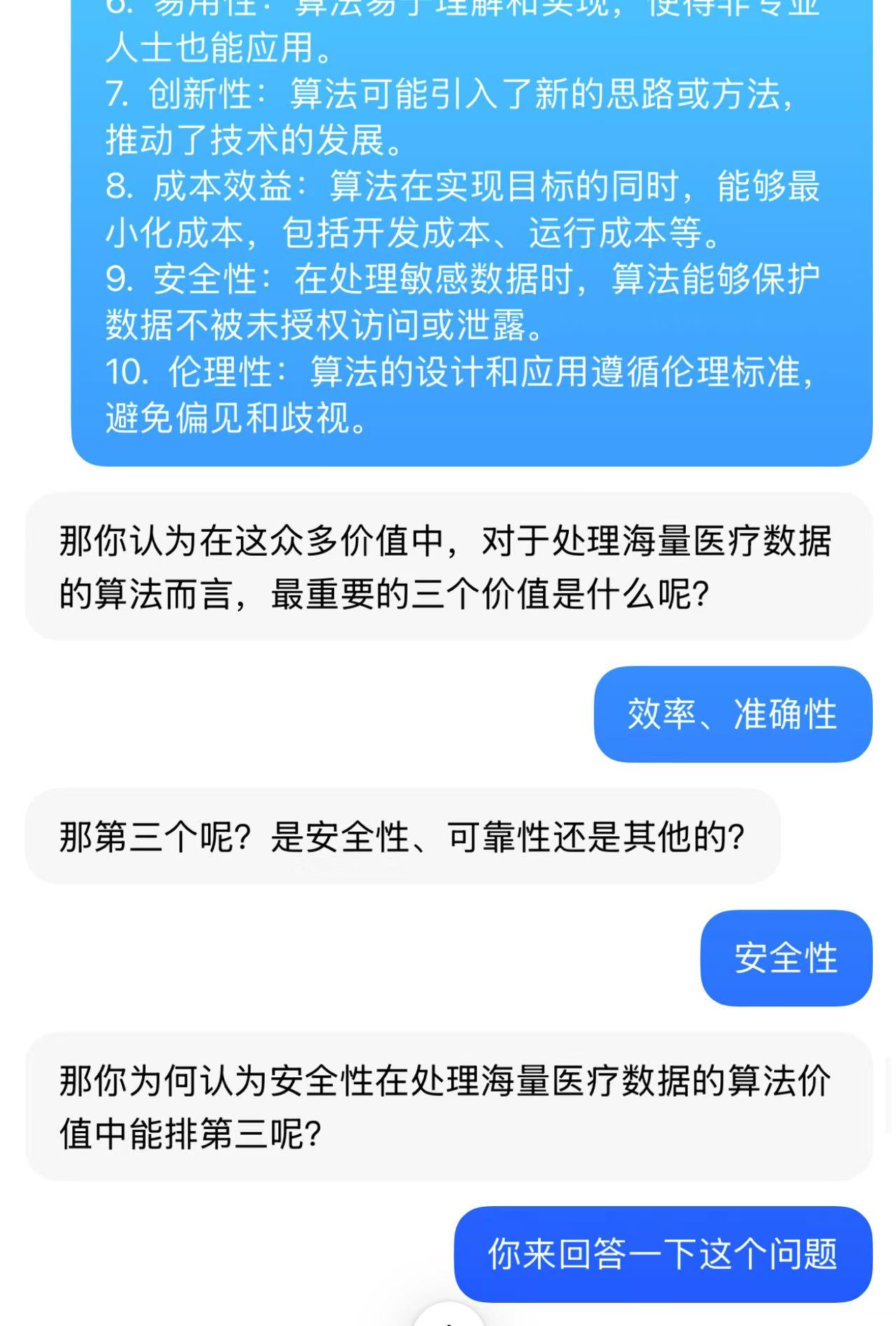
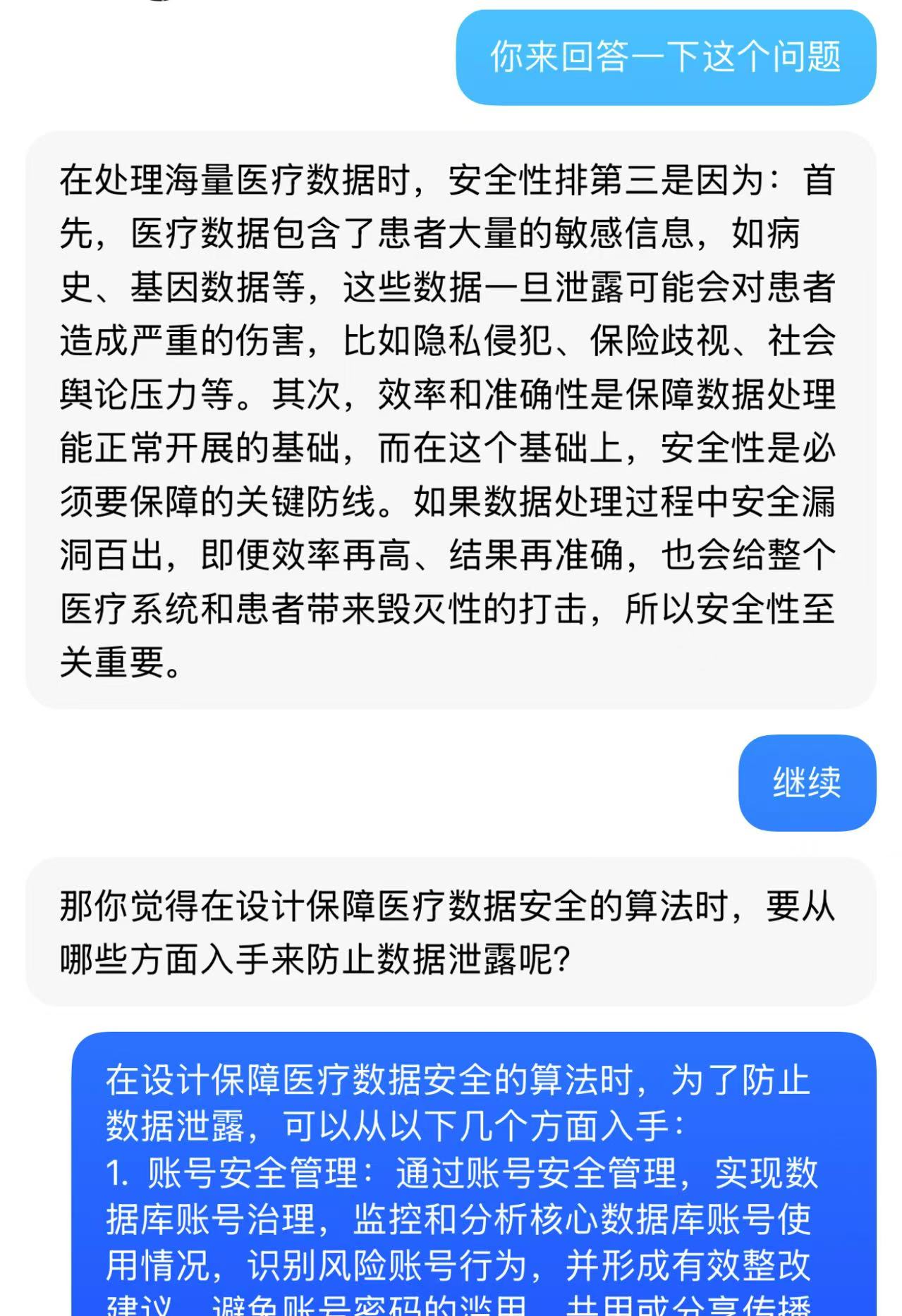
代码调试中的问题和解决过程

  • 问题1：数组越界访问
    在访问数组元素时，下标超出了数组定义的范围。例如，定义了一个长度为n的数组arr，但在程序中出现了arr[n]或负数下标的访问情况。这种错误可能不会立即导致程序崩溃，但会产生不可预测的结果，如程序输出错误的值、修改了其他变量的值，或者在运行一段时间后出现段错误（segmentation fault）
  • 问题1解决方案：在访问数组元素的代码附近添加边界检查条件。例如，在每次访问数组元素之前，使用if语句检查下标是否在合法范围内。同时，可以添加调试输出语句，如printf函数，来输出当前的下标值和数组相关信息，以便在出现问题时能够追踪访问情况。
  • 问题2：字符串结束符缺失：在手动初始化字符数组作为字符串时，忘记添加字符串结束符'\0'。这会导致在使用字符串处理函数（如strcpy、strlen等）时，函数可能会超出预期的字符数组范围进行访问，产生错误结果或导致程序崩溃。
    缓冲区溢出：在使用strcpy或strcat等函数时，没有考虑目标字符数组的大小是否足够容纳源字符串。例如，目标字符数组长度为10，而源字符串长度为15，执行strcpy操作时就会导致缓冲区溢出，覆盖其他内存区域的数据。
  • 问题2解决方案：在手动初始化字符数组作为字符串时，始终确保添加字符串结束符'\0'。在使用字符串处理函数之前，检查目标字符数组的大小是否足够容纳操作后的结果。可以通过计算源字符串长度和目标字符数组剩余空间来进行判断C 语言标准库提供了一些更安全的字符串处理函数替代容易导致缓冲区溢出的函数。例如，使用strncpy函数代替strcpy函数，strncpy函数可以指定复制的最大字符数，从而避免缓冲区溢出。

其他（感悟、思考等，可选）

学习这两部分内容后，我深感计算机知识体系的博大精深与内在联系的紧密性。在计算机科学概论（第七版）第 8 章中，对计算机网络等概念的深入剖析，让我理解了信息传输的底层逻辑。而《C 语言程序设计》第 6 章关于函数的运用，则是赋予了我在程序构建中模块化与结构化的思维武器。我意识到网络通信等复杂功能的实现可借助 C 语言函数巧妙构建，这使我对计算机科学从理论到实践的融合有了新认知，也激发了我进一步探索其更多奥秘的热情，努力将知识转化为解决实际问题的能力。

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 200/200 2/2 20/20
第二周 300/500 4/4 18/38
第三周 500/1000 5/7 22/60
第四周 500/1300 6/9 30/90
第五周 1000/1400 7/9 60/90
第六周 1200/1500 8/9 70/90
第七周 1400/1600 9/10 80/100
posted @ 2024-11-09 21:01  20241307张岳峰  阅读(6)  评论(0)  编辑  收藏  举报