luoguP1288 取数游戏II [博弈论]
题目描述
有一个取数的游戏。初始时,给出一个环,环上的每条边上都有一个非负整数。这些整数中至少有一个0。然后,将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏,两人轮流取数,取数的规则如下:
(1)选择硬币左边或者右边的一条边,并且边上的数非0;
(2)将这条边上的数减至任意一个非负整数(至少要有所减小);
(3)将硬币移至边的另一端。
如果轮到一个玩家走,这时硬币左右两边的边上的数值都是0,那么这个玩家就输了。
如下图,描述的是Alice和Bob两人的对弈过程,其中黑色节点表示硬币所在节点。结果图(d)中,轮到Bob走时,硬币两边的边上都是0,所以Alcie获胜。
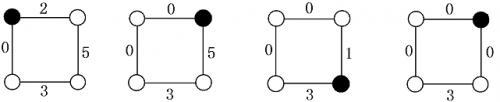
(a)Alice (b)Bob (c)Alice (d)Bob
现在,你的任务就是根据给出的环、边上的数值以及起点(硬币所在位置),判断先走方是否有必胜的策略。
输入输出格式
输入格式:
第一行一个整数N(N≤20),表示环上的节点数。
第二行N个数,数值不超过30,依次表示N条边上的数值。硬币的起始位置在第一条边与最后一条边之间的节点上。
输出格式:
仅一行。若存在必胜策略,则输出“YES”,否则输出“NO”。
输入输出样例
【输入1】 4 2 5 3 0 【输入2】 3 0 0 0
【输出1】 YES 【输出2】 NO
无限手膜,手膜而死。
不过正确性还是够用的。
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 using namespace std; 5 6 const int maxn=25; 7 8 int n; 9 int a[maxn]; 10 11 int main(){ 12 scanf("%d",&n); 13 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 14 for(int i=1;i<=n;i++) 15 if(!a[i]) 16 if(!(i&1)){ 17 puts("YES"); 18 return 0; 19 } 20 else break; 21 for(int i=n;i;i--) 22 if(!a[i]) 23 if((n-i)&1){ 24 puts("YES"); 25 return 0; 26 } 27 else break; 28 puts("NO"); 29 return 0; 30 }
__stdcall的博弈搜索好强啊
参(chao)考(xi)一下他的solution
首先尝试无脑的博弈搜索,60分
然后开始想优化。。。
对于状态0*0,*表示当前处在的位置,是我们知道的第一个必败状态
那么对于状态0*n 0,就是必胜状态,对称的时候同理
然后0*1 n 0就是必败状态,因为只能转移到0*n 0
我们还知道0 n*m 0是必胜状态
所以0*n m 0就是必败状态,因为只能转移到0*n 0(必胜)和0 a*b 0(必胜)
于是0*a b c 0就是必胜状态,0 a*b c 0是必胜状态
所以0*a b c d 0是必败状态
由以上可得知,对于0*a b c d e...0的状态,如果两个0中间的长度为偶数,必败,长度为奇数,必胜
然后对于任意的0 a*...和...*a 0的状态,必胜
然而还是TLE三个点啊。。。继续分析吧
好像有一个很简单的优化,根据上面的分析得知
如果当前状态是0 a b...*...c d 0
这时候可以选择把左边相邻状态变为0或者把右边相邻的变为0
如果这两种有一个必败状态,则此状态必胜
过了。。。大成功。
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 #include <cstring> 5 #include <vector> 6 using namespace std; 7 int n; 8 int a[25]; 9 int next( int idx ) { 10 if( idx == n-1 ) return 0; 11 else return idx+1; 12 } 13 int prior( int idx ) { 14 if( idx == 0 ) return n-1; 15 else return idx-1; 16 } 17 bool dfs( int idx ) { 18 if( a[idx] == 0 && a[prior(idx)] == 0 ) return false; 19 if( a[idx] != 0 && a[next(idx)] == 0 ) return true; 20 if( a[prior(idx)] != 0 && a[prior(prior(idx))] == 0 ) return true; 21 if( a[idx] == 0 ) { // 确定状态,右边为0 22 int cnt = 0; 23 for( int i = prior(idx) ; a[i] != 0 ; i = prior(i) ) ++cnt; 24 if( (cnt&1) ) return true; 25 else return false; 26 } 27 if( a[prior(idx)] == 0 ) { 28 int cnt = 0; 29 for( int i = idx ; a[i] != 0 ; i = next(i) ) ++cnt; 30 if( (cnt&1) ) return true; 31 else return false; 32 } 33 // 把右边变为0 34 int tmp = a[idx]; a[idx] = 0; 35 if( dfs(next(idx)) == false ) { 36 a[idx] = tmp; 37 return true; 38 } 39 a[idx] = tmp; 40 // 把左边变为0 41 tmp = a[prior(idx)]; a[prior(idx)] = 0; 42 if( dfs(prior(idx)) == false ) { 43 a[prior(idx)] = tmp; 44 return true; 45 } 46 a[prior(idx)] = tmp; 47 // 其他的各种尝试 48 for( int i = 1 ; i < a[idx] ; ++i ) { 49 a[idx] -= i; 50 if( dfs(next(idx)) == false ) { 51 a[idx] += i; 52 return true; 53 } 54 a[idx] += i; 55 } 56 for( int i = 1 ; i < a[prior(idx)] ; ++i ) { 57 a[prior(idx)] -= i; 58 if( dfs(prior(idx)) == false ) { 59 a[prior(idx)] += i; 60 return true; 61 } 62 a[prior(idx)] += i; 63 } 64 return false; 65 } 66 int main() { 67 scanf( "%d" , &n ); 68 for( int i = 0 ; i < n ; ++i ) scanf( "%d" , &a[i] ); 69 if( dfs(0) ) printf( "YES\n" ); 70 else printf( "NO\n" ); 71 return 0; 72 }




