[luogu P3384] 【模板】树链剖分 [树链剖分]
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
输入输出样例
输入样例#1:
5 5 2 24 7 3 7 8 0 1 2 1 5 3 1 4 1 3 4 2 3 2 2 4 5 1 5 1 3 2 1 3
输出样例#1:
2 21
说明
时空限制:1s,128M
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=1000,M<=1000
对于100%的数据:N<=100000,M<=100000
(其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233)
样例说明:
树的结构如下:
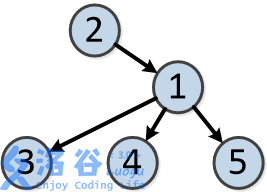
各个操作如下:
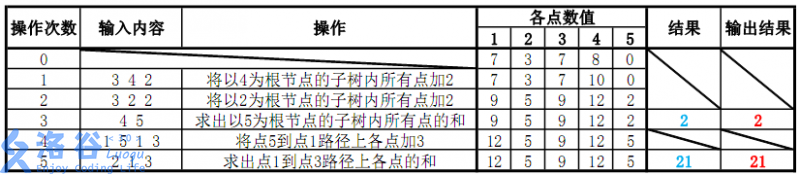
故输出应依次为2、21(重要的事情说三遍:记得取模)
My Solution
哪来的什么solution
因为这题快颓了week了
统计:2/29 AC!!!
为什么我之前要用树状数组嘞
向unsigned大佬低头 orz
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 using namespace std; 5 6 typedef long long ll; 7 8 inline int read(){ 9 char ch; 10 int re=0; 11 bool flag=0; 12 while((ch=getchar())!='-'&&(ch<'0'||ch>'9')); 13 ch=='-'?flag=1:re=ch-'0'; 14 while((ch=getchar())>='0'&&ch<='9') re=re*10+ch-'0'; 15 return flag?-re:re; 16 } 17 18 inline ll rea(){ 19 char ch; 20 ll re=0; 21 bool flag=0; 22 while((ch=getchar())!='-'&&(ch<'0'||ch>'9')); 23 ch=='-'?flag=1:re=ch-'0'; 24 while((ch=getchar())>='0'&&ch<='9') re=re*10+ch-'0'; 25 return flag?-re:re; 26 } 27 28 struct edge{ 29 int to,next; 30 edge(int to=0,int next=0): 31 to(to),next(next){} 32 }; 33 34 struct Segment_Tree{ 35 int l,r; 36 ll sum,tag; 37 }; 38 39 const int maxn=100001; 40 41 int cnt,n,m,root; 42 ll mod; 43 edge edges[maxn<<1]; 44 Segment_Tree tre[maxn<<2]; 45 int head[maxn],top[maxn],dep[maxn],fat[maxn],id[maxn],id_[maxn],son[maxn],siz[maxn]; 46 int data[maxn]; 47 48 inline void add_edge(int from,int to){ 49 edges[++cnt]=edge(to,head[from]); head[from]=cnt; 50 edges[++cnt]=edge(from,head[to]); head[to]=cnt; 51 } 52 53 void init(){ 54 n=read(); m=read(); root=read(); mod=rea(); 55 for(int i=1;i<=n;i++) 56 data[i]=read(); 57 int from,to; 58 cnt=0; 59 for(int i=1;i<n;i++){ 60 from=read(); to=read(); 61 add_edge(from,to); 62 } 63 } 64 65 void dfs_1(int x,int fa){ 66 fat[x]=fa; 67 siz[x]=1; 68 dep[x]=dep[fa]+1; 69 for(int ee=head[x];ee;ee=edges[ee].next) 70 if(edges[ee].to!=fa){ 71 dfs_1(edges[ee].to,x); 72 siz[x]+=siz[edges[ee].to]; 73 if(!son[x]||siz[edges[ee].to]>siz[son[x]]) 74 son[x]=edges[ee].to; 75 } 76 } 77 78 void dfs_2(int x,int fa){ 79 if(!son[x]) return; 80 top[son[x]]=top[x]; 81 id[son[x]]=++cnt; 82 id_[cnt]=son[x]; 83 dfs_2(son[x],x); 84 for(int ee=head[x];ee;ee=edges[ee].next) 85 if(edges[ee].to!=fa&&edges[ee].to!=son[x]){ 86 top[edges[ee].to]=edges[ee].to; 87 id[edges[ee].to]=++cnt; 88 id_[cnt]=edges[ee].to; 89 dfs_2(edges[ee].to,x); 90 } 91 } 92 93 inline void push_up(int x){ 94 tre[x].sum=tre[x<<1].sum+tre[x<<1|1].sum; 95 } 96 97 inline void push_down(int x){ 98 tre[x<<1].tag+=tre[x].tag; 99 tre[x<<1].sum+=tre[x].tag*(tre[x<<1].r-tre[x<<1].l+1); 100 tre[x<<1|1].tag+=tre[x].tag; 101 tre[x<<1|1].sum+=tre[x].tag*(tre[x<<1|1].r-tre[x<<1|1].l+1); 102 tre[x].tag=0; 103 return; 104 } 105 106 void build(int x,int l,int r){ 107 tre[x].l=l; tre[x].r=r; 108 if(l==r){ 109 tre[x].sum=data[id_[l]]; 110 return; 111 } 112 int mid=(l+r)>>1; 113 build(x<<1,l,mid); 114 build(x<<1|1,mid+1,r); 115 push_up(x); 116 } 117 118 void make(){ 119 dfs_1(root,0); 120 cnt=1; 121 top[root]=root; 122 id[root]=cnt; 123 id_[cnt]=root; 124 dfs_2(root,0); 125 build(1,1,n); 126 } 127 128 void update(int x,int L,int R,ll c){ 129 if(L<=tre[x].l&&tre[x].r<=R){ 130 tre[x].tag+=c; 131 tre[x].sum+=c*(tre[x].r-tre[x].l+1); 132 return; 133 } 134 push_down(x); 135 int mid=(tre[x].l+tre[x].r)>>1; 136 if(R<=mid) update(x<<1,L,R,c); 137 else if(L>mid) update(x<<1|1,L,R,c); 138 else{ 139 update(x<<1,L,mid,c); 140 update(x<<1|1,mid+1,R,c); 141 } 142 push_up(x); 143 } 144 145 ll query_sum(int x,int L,int R){ 146 if(L<=tre[x].l&&tre[x].r<=R) 147 return tre[x].sum; 148 push_down(x); 149 int mid=(tre[x].l+tre[x].r)>>1; 150 if(R<=mid) return query_sum(x<<1,L,R); 151 else if(L>mid) return query_sum(x<<1|1,L,R); 152 else return query_sum(x<<1,L,mid)+query_sum(x<<1|1,mid+1,R); 153 } 154 155 void change(int u,int v,ll c){ 156 int f1=top[u]; 157 int f2=top[v]; 158 while(f1!=f2){ 159 // this ensure u and v is not at the same heavy chain 160 if(dep[f1] < dep[f2]){ 161 // ensure that heavy chain 1 is under heavy chain 2 162 swap(f1,f2); 163 swap(u,v); 164 } 165 update(1,id[f1],id[u],c); 166 u=fat[f1]; 167 f1=top[u]; 168 } 169 if(dep[u]>dep[v]) swap(u, v); 170 update(1,id[u],id[v],c); 171 } 172 173 ll find_sum(int u, int v) 174 { 175 ll sum=0; 176 int f1=top[u]; 177 int f2=top[v]; 178 while(f1!=f2) 179 { 180 if(dep[f1]<dep[f2]) 181 { 182 swap(f1,f2); 183 swap(u,v); 184 } 185 sum+=query_sum(1,id[f1],id[u]); 186 sum%=mod; 187 u=fat[f1]; 188 f1=top[u]; 189 } 190 if(dep[u]>dep[v]) swap(u, v); 191 sum+=query_sum(1,id[u],id[v]); 192 return sum%mod; 193 } 194 195 void solve(){ 196 int opt,ss,tt; 197 ll c; 198 for(int i=0;i<m;i++){ 199 opt=read(); 200 if(opt&1){ 201 //opt==3 202 if(opt&2){ 203 ss=read(); c=rea(); 204 update(1,id[ss],id[ss]+siz[ss]-1,c); 205 } 206 //opt==1 207 else{ 208 ss=read(); tt=read(); c=rea(); 209 change(ss,tt,c); 210 } 211 } 212 else{ 213 //opt==4 214 if(opt&4){ 215 ss=read(); 216 printf("%lld\n",query_sum(1,id[ss],id[ss]+siz[ss]-1)%mod); 217 } 218 //opt==2 219 else{ 220 ss=read(); tt=read(); 221 printf("%lld\n",find_sum(ss,tt)); 222 } 223 } 224 } 225 } 226 227 int main(){ 228 //freopen("data.in","r",stdin); 229 init(); 230 make(); 231 solve(); 232 return 0; 233 }
爱你锋利的伤痕 爱你成熟的天真



