【以练促学：数据结构】3.栈和队列

（持续刷题，持续更新...）

1. 栈的基本操作

• 栈的基本操作主要包括：置空栈、判断栈空、进栈、出栈、取栈顶元素
• 进栈：指针先+1，元素再入栈
  • top = -1，[++top]
  • top = 0，[top++]
• 出栈：元素先出栈，指针再-1
  • top = -1，[top--]
  • top = 0，[--top]

 

eg：（  ）不是栈的基本操作

A. 删除栈顶元素

B. 删除栈底元素

C. 判断栈是否为空

D. 将栈置为空栈

 // 基本操作是指结构中最核心、最基本的运算；删除栈底元素的实现比较复杂，不算基本的操作

 

eg：假定利用数组 a[n] 顺序存储一个栈，用 top 表示栈顶指针，用 top == -1 表示栈空，并已知栈未满，当元素 x 进栈时所执行的操作为（  ）

A. a[--top] = x

B. a[top--] = x

C. a[++top] = x

D. a[top++] = x

 // 前置是先加后赋值，后置是先赋值再加。进栈是指针先+1，元素再进栈；故 ++top

 

eg：若栈 S1 中保存整数，栈 S2 中保存运算符，函数 F() 依次执行下述各步操作：

         1. 从 S1 中依次弹出两个操作数 a、b

         2. 从 S2 中弹出一个运算符 op

         3. 执行相应的运算 b  op  a

         4. 将运算结果压入 S1 中

假定 S1 中的操作数依次是：5、8、3、2（2在栈顶），S2 中的运算符依次是：*、-、+（+在栈顶）。则调用3次函数 F() 后，S1 栈顶保存的值是（  ）

A. -15

B. 15

C. -20

D. 20

 //  注意题中是弹出 a、b，但运算执行：b op a，不要想当然的用惯性 a op b

 

 

 

2. 栈的元素输出

• 卡特兰数：n个元素进栈，则出栈元素不同排列的个数为：（1/n+1）*Cⁿ_2n
  • eg：5个元素进栈，则出栈元素不同排列的个数为：C⁵_2*5 = （10*9*8*7*6 / 6*5*4*3*2*1）= 42 种
• 规律的输出情况：n-i+1
• 不规律的输出情况：按栈的 “先进后出” 原则，需要具体分析

 

eg：若一个栈的输入序列是 1，2，3，...，n，输出序列的第一个元素是 n，则第 i 个输出元素是（  ）

A. 不确定

B. n-i

C. n-i-1

D. n-i+1

 //  输出的第一个元素是 n；对应第二个元素 n-1；第三个元素 n-2；第四个元素 n-3；第 i 个元素 n-i+1；

 

eg：若一个栈的输入序列是 1，2，3，...，n，输出序列的第一个元素是 i，则第 j 个输出元素是（  ）

A. i-j-1

B. i-j

C. j-i+1

D. 不确定

 //  因为不确定输出的第一个元素是啥，所以就不确定第 j 个输出元素了

 

eg：一个栈的入栈序列是 1，2，3，...，n，出栈序列是 P₁，P₂，P₃，...，P_n，若 P₂ = 3，则 P₃ 可能取值的个数是（  ）

A. n-3

B. n-2

C. n-1

D. 不确定

 //  若 P₂ = 3，则 P₃ 可以取后面的 4，5，6，...，n 和 2。若 P₂ = 3，则 P₃ = 1 的情况：进栈 1，2 后出栈 2，则 P₁ = 2；进栈 3 后出栈 3，则 P₂ = 3；出栈 1，则 P₃ = 1。所以综上，除了 3 以外，所以数都可能被 P₃ 取，故是 n-1 种可能

 

 

3. 共享栈

•  “上溢”：栈满时，再做进栈运算产生的空间溢出
•  “下溢”：栈空时，再做出栈运算产生的溢出

 

eg：采用共享栈的好处（  ）

A. 减少存取时间，降低发生上溢的可能

B. 节省存储空间，降低发生上溢的可能

C. 减少存取时间，降低发生下溢的可能

D. 节省存储空间，降低发生下溢的可能

 //  栈中元素的存取时间都是 O(1)，共享栈不会减少存取时间。共享栈是为节省空间，只可能发生 “上溢”（栈顶指针超出了最大范围）

 

 

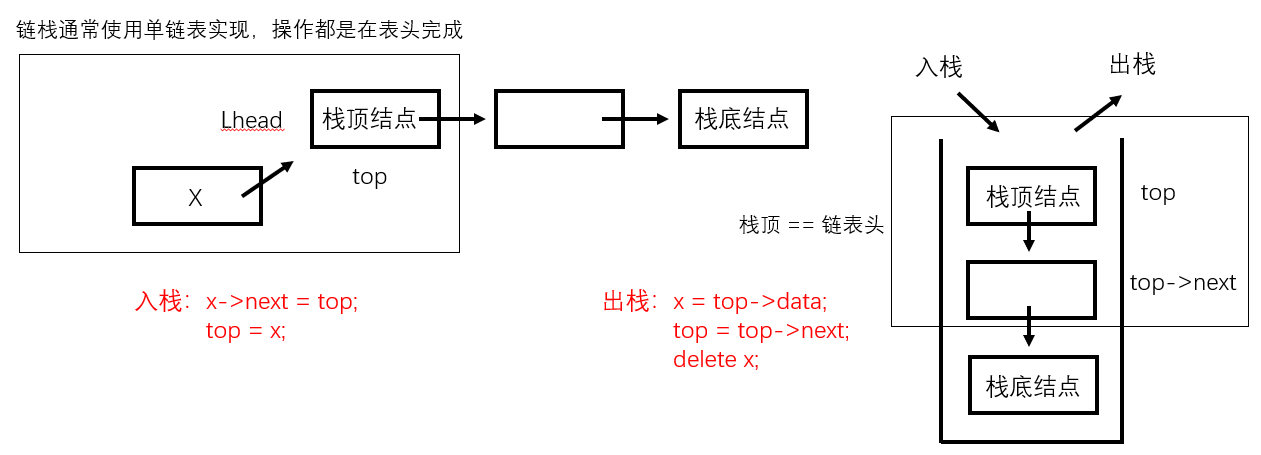
4. 链栈

• 和顺序栈相比，链栈通常不会出现栈满的情况（只有当内存无可用空间时才会栈满）
• 链栈的入栈和出栈操作都在链表的头进行
  • 入栈（Push 操作）
    • x->next = top;
    • top = x;

• • 出栈（Pop 操作）
    • x = top->data;
    • top = top->next;

 

 

 

 

eg：设链表不带头结点，且所有操作均在表头进行，则下列最不适合作为链栈的是（  ）

A. 只有表头结点指针，没有表尾指针的 双向循环链表

B. 只有表尾结点指针，没有表头指针的 双向循环链表

C. 只有表头结点指针，没有表尾指针的 单向循环链表

D. 只有表尾结点指针，没有表头指针的 单向循环链表

 

 // 链栈由单链表实现，入栈和出栈都是在表头进行的，双向链表因为是双向的（废话），不管是表头指针还是表尾指针，都可以很方便的找到表头，所以双向循环链表都很适合。而单向循环链表的尾指针也可以方便的找到头

 

eg：向一个栈顶指针为 top 的链栈中插入一个 x 结点，则执行（  ）

A. top->next = x

B. x->next = top->next;    top->next = x

C. x->next = top;    top = x

D.  x->next = top;    top = top->next

 //  入栈（Push 操作）：x->next = top;    top = x;

 

eg：链栈执行 Pop 操作，并将出栈的元素存在 x 中，应该执行（  ）

A. x = top;    top = top->next

B. x = top->data

C. top = top->next;    x = top->data

D. x = top->data;    top = top->next; 

 //  出栈（Pop 操作）：x = top->data;    top = top->next;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.