数论1.0 (基础知识)
今天,ZUTTER终于下定决心去学了数论,然后

从基础说起
-
gcd
这个..感性理解一下就好了啊
gcd(int a,int b)
{
if(b==0) return a;
return(b,a%b);
}
-
exgcd
扩展欧几里得算法,用于在已知(a,b)时求解(x,y) 使 ax+by=c (c | gcd(a,b))
void exgcd(ll a, ll b, ll& x, ll& y, ll& c)
{
if(!b) {y = 0; x = 1; return c;}
int d=exgcd(b, a % b, y, x);
y -= a / b * x; return d;
}
证明:
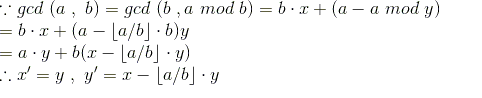
又因为 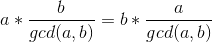
所以任意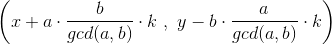 都可为解
都可为解
-
排列
求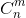 %P
%P
- \(C_n^m=C_{n-1}^{m-1}+C_{n-1}^{m}\)
m,n小于p时可以用O(n)的时间预处理阶乘和阶乘逆元,然后O(1) 求值
当m,n过大p过小,m,n>p 时
-
卢卡斯定理
求c的公式 \(C_n^m=C_{n/p}^{m/p}\times C_{n\%p}^{m\%p}\)
递归中每次当 m,n<p 时调用1中公式即可。
二项式定理
\((x+y)^n\) 中 \(x^ty^{n-t}\) 的系数为 \(C_n^t\)
-
中国剩余定理 Chinese Rimainder Theorem
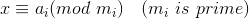
解法:
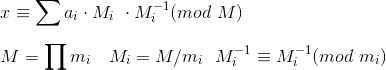
比较两个CRT下整数
中国剩余定理 (Chinese Remainder Theorem, CRT) 可求解如下形式的一元线性同余方程组(其中\(n\) 两两互质):

假设一中进制可以表示成
\(x=b_1+b_2\times2+b_3\times 2\times 3+...\)
然后左右两端同时
\(\mod n_1\ a_1=b_1\)
\(\mod n_2\ a_2=b_1+b_2n_1\)
$\mod n_3\ a $
然后从大往小比较就行
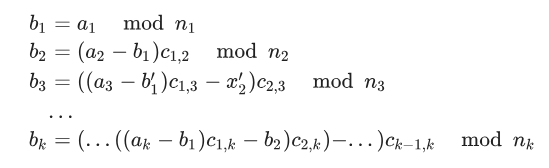
-
博弈Nim
有\(n\)堆木棒,每堆中木棒数量为\(K_i\),两个人轮流取木棒,每次不能同时取两堆中的木棒也不能不取,取到最后一根木棒的人获胜,问对于当前状况是否是先手必胜局面。
结论:若对于\(k_1 \bigoplus k_2 \bigoplus k_3 \bigoplus ... \bigoplus k_n\ !=0\) 都是先手必胜
证明:咕咕咕(逃
-
第二类斯特林数S,
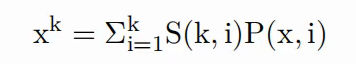
S(n,x)表示把n个数分成x组的方案数
康托展开
公式 $$A_n\times (n-1)!+A_{n-1}\times (n-2)!+...+A_1\times 0!$$
其中\(A_i\)代表第\(i\)个数后比这个数小的数的个数
预处理阶乘后可以 \(O(n)\)求解
可以逆运算
逆元
当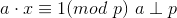 时,称x为a在%p意义下的逆元,记作
时,称x为a在%p意义下的逆元,记作 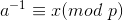
解法:
-
扩展欧几里得
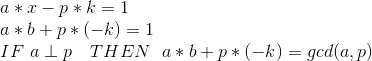
-
费马小定理
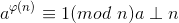 且
且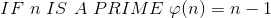
-
线性求逆元
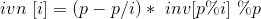
-
裴蜀定理
除法分块
给定正整数\(n ,k\)计算\(\sum_{i=1}^nk\%i\)
原式可变为\(n*k-\sum^n_{i=1}\left \lfloor k/i \right \rfloor *i\)
\(\because \left \lfloor k/\left \lfloor k/\left \lfloor k/x \right \rfloor \right \rfloor \right \rfloor= \left \lfloor k/x\right \rfloor\)
\(\therefore\forall i\in[x,\left \lfloor k/x\right \rfloor],\left \lfloor k/i\right \rfloor\) 相同
所以答案会被分成\(\sqrt k\)个。
阶
最小的k称为a的阶,记作 \(<a>\)
\(<a>|\phi (n)\)
若 \(<a>=\phi(n),a\)是n的原根
拉格朗日插值
柿子
然后我们把1~d插进去就是
关于边界,如果不能有零就重新推一下不要硬套柿子
立方和公式



 浙公网安备 33010602011771号
浙公网安备 33010602011771号