P2633 Count on a tree

题目描述

给定一棵N个节点的树，每个点有一个权值，对于M个询问(u,v,k)，你需要回答u xor lastans和v这两个节点间第K小的点权。其中lastans是上一个询问的答案，初始为0，即第一个询问的u是明文。

输入输出格式

输入格式：

第一行两个整数N,M。

第二行有N个整数，其中第i个整数表示点i的权值。

后面N-1行每行两个整数(x,y)，表示点x到点y有一条边。

最后M行每行两个整数(u,v,k)，表示一组询问。

输出格式：

M行，表示每个询问的答案。

输入输出样例

输入样例#1： 复制

8 5
105 2 9 3 8 5 7 7
1 2
1 3
1 4
3 5
3 6
3 7
4 8
2 5 1
0 5 2
10 5 3
11 5 4
110 8 2

输出样例#1： 复制

2
8
9
105
7

说明

HINT：

N,M<=100000

暴力自重。。。

来源：bzoj2588 Spoj10628.

---

查找静态区间第k大只需要前缀可持久化权值线段树即可
考虑处理树上区间第k大与序列的区别

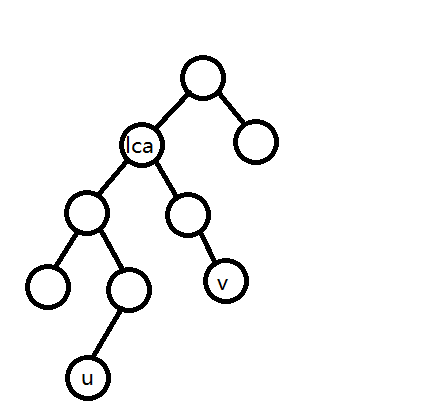
比如要找u->v间的权值第k大，其实是要找u->lca->v之间的权值第k大，而u->lca的权值线段树其实可以用u的权值线段树减father[lca]的权值线段树得到。所以u->lca->v的权值线段树就转变成了u+v-lca-father[lca]
此时我们需要维护的变成了每个点的树上前缀权值线段树。主席树可以做到nlogn的时间和空间

---

#include<iostream>
#include<stdio.h>
#include<algorithm>
#define M 100010
#define update(a) tr[a]=tr[ls[a]]+tr[rs[a]]
using namespace std;

int ans,z,h,de[M],f[M][25],q,x,y,cnt,i,m,n,j,k,a[M],ls[M*20],rs[M*20],g[M],ver[M*3],edge[M*3],nex[M*3],head[M],t[M],pre[M],tr[M*20];
void add(int x,int y)
{
	cnt+=1;
	ver[cnt]=y;
	nex[cnt]=head[x];
	head[x]=cnt;
}

void built(int z,int now,int l,int r,int p)
{
	if(l==r)  
	{
		tr[now]=tr[p]+1;
		return;
	}
	int mid=(l+r)/2;
	if(z<=mid)
	{
		rs[now]=rs[p];
		cnt+=1;	ls[now]=cnt;
		built(z,cnt,l,mid,ls[p]);
		update(now);
	}
	else 
	{
		ls[now]=ls[p];
		cnt+=1; rs[now]=cnt;
		built(z,cnt,mid+1,r,rs[p]);
		update(now);
	}
}

void dfs1(int x,int fa)
{
	f[x][0]=fa; cnt+=1;
	g[x]=cnt;	de[x]=de[fa]+1;
	built(a[x],cnt,1,m,g[fa]);
	for(int i=head[x];i;i=nex[i]) if(ver[i]!=fa) dfs1(ver[i],x);
}

void built1(int now,int l,int r)
{
	if(l==r) return;
	cnt+=1;
	ls[now]=cnt;
	built1(ls[now],l,(l+r)/2);
	cnt+=1;
	rs[now]=cnt;
	built1(rs[now],(l+r)/2+1,r);
}

int lca(int x,int y)
{
	if(de[x]<de[y]) swap(x,y);
	for(int i=20;i>=0;i--)	
		if(de[f[x][i]]>=de[y]) x=f[x][i];
	for(int i=20;i>=0;i--)  if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
	if(x!=y) return f[x][0];
	else return x;
}

int search(int x,int y,int l,int d,int z,int ll,int rr)
{
	if(ll==rr) return ll;
	int w=tr[ls[x]]+tr[ls[y]]-tr[ls[l]]-tr[ls[d]],u=tr[rs[x]]+tr[rs[y]]-tr[rs[l]]-tr[rs[d]];
	if(w>=z) return search(ls[x],ls[y],ls[l],ls[d],z,ll,(ll+rr)/2);
	return search(rs[x],rs[y],rs[l],rs[d],z-w,(ll+rr)/2+1,rr);
}

int main()
{
	scanf("%d%d",&n,&q);
	for(i=1;i<=n;i++) scanf("%d",&a[i]),t[i]=a[i];
	
	sort(t+1,t+1+n);
	m=unique(t+1,t+1+n)-t-1;
	for(i=1;i<=n;i++) 
	{
		k=lower_bound(t+1,t+1+m,a[i])-t;
		pre[k]=a[i];
		a[i]=k;
	}
	
	for(i=1;i<n;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y); add(y,x);
	}
	g[0]=cnt=1; 
	built1(1,1,m);
	dfs1(1,0);
	
	for(i=1;i<=20;i++) 
		for(j=1;j<=n;j++) f[j][i]=f[f[j][i-1]][i-1];
		
	for(i=1;i<=q;i++)
	{
		scanf("%d%d%d",&x,&y,&z);
		x=x^ans;
		h=lca(x,y);
		ans=pre[search(g[x],g[y],g[h],g[f[h][0]],z,1,m)];
		printf("%d\n",ans);
	}
}