Wannafly挑战赛27

于是说好带我上分拿购物卡的asuldb神仙自己咕咕掉分了
还好我rateing低 ~(～￣▽￣)～

---

链接：B
来源：牛客网

给出一棵仙人掌(每条边最多被包含于一个环，无自环，无重边，保证连通)，要求用最少的颜色对其顶点染色，满足每条边两个端点的颜色不同，输出最小颜色数即可

---

结论：ans=1/2/3
没有边ans=1， 没有三角形ans=2，否则ans=3

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define max(a,b) ((a)>(b)? (a):(b))
#define min(a,b) ((a)<(b)? (a):(b))

using namespace std;
int i,m,n,j,k,a[1000001],ver[1000001],edge[1000001],nex[1000001],cnt,d[1000001],head[1000001],x,y;

void add(int x,int y)
{
	cnt+=1;
	ver[cnt]=y; nex[cnt]=head[x]; head[x]=cnt;
}

bool dfs(int now)
{
	for(int i=head[now];i;i=nex[i])
	{
		int t=ver[i];
		if(d[t]==d[now]) return 0;
		if(!d[t])
        {
            d[t]=d[now]%2+1;
            if(!dfs(t)) return 0;
        }
	}
	return 1;
}

int main()
{
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	if(n==0)
	{
		printf("0");
		return 0;
	}
	if(m==0) 
	{
		printf("1");
		return 0;
	}
	d[1]=1;
	if(dfs(1)) printf("2");
	else printf("3");
}

---

链接：C
来源：牛客网

给出一棵树，求有多少种删边方案，使得删后的图每个连通块大小小于等于k，两种方案不同当且仅当存在一条边在一个方案中被删除，而在另一个方案中未被删除，答案对998244353取模

---

卡常！卡常！！卡常！！！严重卡常！！！！！


这是第一次提交能跑出正解
然后

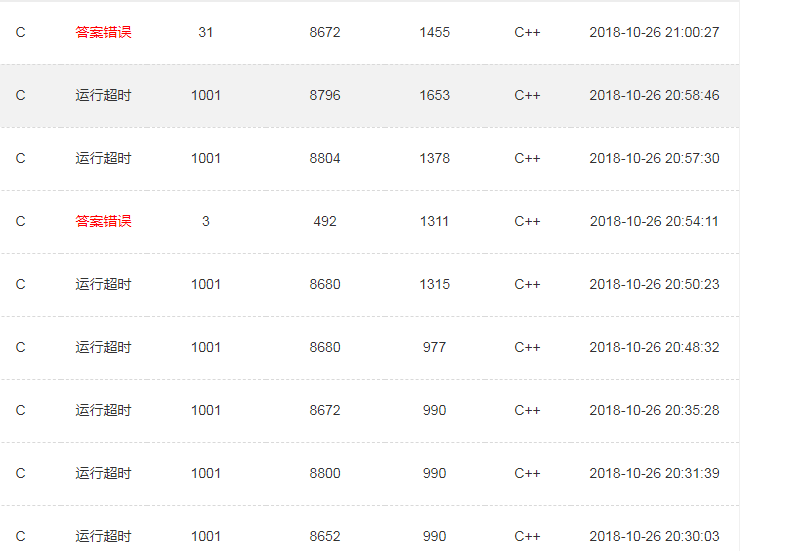
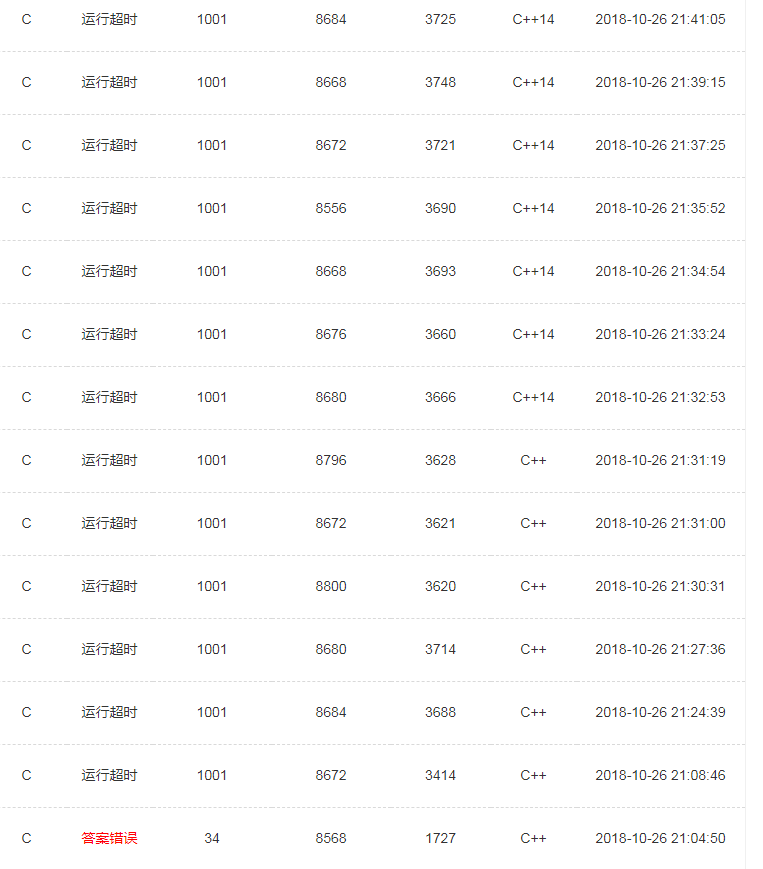
写题1h卡常1.5h

---

所以这个sxbk的程序张这样

#pragma GCC diagnostic error "-std=c++14"
#pragma GCC target("avx")
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define LL long long
#define M 998244353
#define RI register int
#define max(a,b) ((a)>(b)? (a):(b))
#define min(a,b) ((a)<(b)? (a):(b))
   
using namespace std;
   
int m,n,k,f[2001][2001], head[4001], nex[4001], ver[4001], cnt,s[4001],x,y,ans;
   
inline void add(int x,int y)
{
    cnt+=1;
    ver[cnt]=y; nex[cnt]=head[x]; head[x]=cnt;
}
   
   
inline char gc()
{
    static char now[1<<22],*S,*T;
    if (T==S)
    {
        T=(S=now)+fread(now,1,1<<22,stdin);
        if (T==S) return EOF;
    }
    return *S++;
}
inline int read()
{
    register int x=0,f=1;
    register char ch=gc();
    while(!isdigit(ch))
    {
        if (ch=='-') f=-1;
        ch=gc();
    }
    while(isdigit(ch)) x=(x<<1)+(x<<3)+ch-'0',ch=gc();
    return x*f;
}
   
void dfs(int now,int fa)
{
    s[now]=1;
    f[now][1]=1;
    for(RI i=head[now];i;i=nex[i])
    {
        int t=ver[i];
        if(t==fa) continue;
        dfs(t,now);
        s[now]+=s[t];
        for(RI j=min(s[now],k);j>0;--j)
        {
            if(f[t][0]!=0 &&f[t][0]!=1) f[now][j]=((LL)f[now][j]*f[t][0])%M;
            if(j==1) continue;
            for(RI l=1;l<=min(s[t],j-1);++l)
            {
                if(f[now][j-l]==0 || f[t][l]==0) continue;
                int o=(LL)f[now][j-l]*f[t][l]%M;
                if(f[now][j]+o<M) f[now][j]=(f[now][j]+o);
                else f[now][j]=f[now][j]+o-M;
            }
        }
    }
       
    for(RI i=1;i<=min(s[now],k);++i)
    {
        if(!f[now][i]) break;
        if(f[now][0]+f[now][i]<M) f[now][0]=f[now][0]+f[now][i];
        else f[now][0]=(f[now][0]+f[now][i])-M;
    }
}
   
int main()
{
    n=read(); k=read();
    for(RI i=1;i<n;++i)
    {
        x=read(); y=read();
        add(x,y); add(y,x);
    }
    dfs(1,0);
  
    printf("%d",f[1][0]);
}

---