莫队
基本计算方法其实就是把区间离线下来以后每次在上次询问区间的基础上把左端点挪一挪，再把右端点挪一挪，记录答案
看起来时间复杂度爆炸啊但是如果离线区间排序优美的话可以做到\(O(n\sqrt n)\)
把整个序列分块，排序的顺序是1.左端点块的编号2.右端点位置
这样的话左右端点就都是最多移动\(n\sqrt n\)次
带修莫队
把时间也设成一维，然后时间负载度不会超过\(O(n^{\frac5 3})\)
排序方法1.左端点块编号2.右端点块编号3.查询前的修改次数
树上莫队
先求树的dfs序
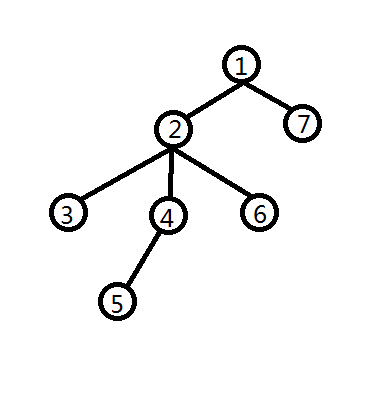
比如↑的就是\(1,2,3,3,4,5,5,4,6,6,2,7,7,1\)每个数都会出现两次，分别是第一次进入（记做\(bg[i]\)）和离开(记做\(ed[i]\))
每次截出一个区间\(ed[x],bg[y]\)，比如\(3\to 6\) 就是\(3,4,5,5,4,6\)，每个位置每出现一次就把它的次数异或1
然后发现这样并不包含lca，所以单独计算lca的贡献就行
当然如果lca就在询问的两个端点中，那么从lca的\(bg\)开始到另一端点的\(bg\)
排序的时候直接把dfs序分块
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define M 3000001
using namespace std;
int b[M],ans,L,R,n,m,k,a[M],ver[M],head[M],nex[M],cnt,inq[M],s[M],top[M],wson[M],e,x,y,dfn[M],cn,f[M],bg[M],ed[M],res[M],al[M],d[M],fa[M];
struct vv{int x,y,id,lca;} q[M];
bool cmp(vv a,vv b){return inq[a.x]==inq[b.x]?a.y<b.y: inq[a.x]<inq[b.x];}
void add(int x,int y)
{
ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt;
ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt;
}
void dfs1(int x,int father)
{
s[x]=1; bg[x]=++cnt, f[cnt]=x;
d[x]=d[father]+1; fa[x]=father;
for(int i=head[x];i;i=nex[i])
{
if(ver[i]==father) continue;
dfs1(ver[i],x); s[x]+=s[ver[i]];
if(s[ver[i]]>s[wson[x]]) wson[x]=ver[i];
}
f[++cnt]=x, ed[x]=cnt;
}
void dfs2(int x,int tt)
{
top[x]=tt;
if(wson[x]) dfs2(wson[x],tt);
for(int i=head[x];i;i=nex[i]) if(!top[ver[i]]) dfs2(ver[i],ver[i]);
}
int lca(int x,int y)
{
if(x>n) return x;
while(top[x]!=top[y])
{
if(d[top[x]]<d[top[y]]) swap(x,y);
x=fa[top[x]];
}
return d[x]>d[y] ? y:x;
}
void solve(int x)
{
if(b[x]) ans+=(!d[a[x]]++);
else ans-=(!--d[a[x]]);
}
int main()
{
scanf("%d%d",&n,&m); e=sqrt(2*n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),al[i]=a[i];
sort(al+1,al+1+n);
int z=unique(al+1,al+1+n)-al-1;
for(int i=1;i<=n;i++) a[i]=lower_bound(al+1,al+1+z,a[i])-al;
for(int i=1;i<=n+n;i++) inq[i]=i/e;
for(int i=1;i<n;i++) scanf("%d%d",&x,&y), add(x,y);
cnt=0; dfs1(1,0); dfs2(1,1); d[0]=1; solve(0);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&x,&y); q[i].id=i;
if(bg[x]>bg[y]) swap(x,y);
int l=lca(x,y);
if(x==l) q[i].x=bg[x], q[i].y=bg[y];
else q[i].x=ed[x], q[i].y=bg[y], q[i].lca=l;
}
sort(q+1,q+1+m,cmp); memset(d,0,sizeof(d));
for(int i=1;i<=m;i++)
{
while(L<q[i].x) b[f[L]]^=1, solve(f[L]), L+=1;
while(L>q[i].x) b[f[--L]]^=1, solve(f[L]);
while(R<q[i].y) b[f[++R]]^=1, solve(f[R]);
while(R>q[i].y) b[f[R]]^=1, solve(f[R]), R-=1;
if(q[i].lca && !d[a[q[i].lca]]) res[q[i].id]=ans+1;
else res[q[i].id]=ans;
}
for(int i=1;i<=m;i++) printf("%d\n",res[i]);
}
回滚莫队
有些东西可以轻松插入但是没法删除（比如区间max
这是后就要掏出不需要删除的回滚莫队
像普通莫队一样把询问排序（不要奇偶优化）然后按照左端点一块一块的转移
特判掉左右端点在同一块的询问，剩下的先钦定左右端点都在当前块的右端
把右端点从左往右扫，遇到询问再把左端点往左扫并记录修改操作，记录答案以后再改回来
时间复杂度还是\(O(n\sqrt n)\)但是常数大了许多
二次离线莫队
用于解决询问区间两两关系的问题，要求对于已处理处前缀信息，可以算x与前缀的贡献和
\(f(i,j)\) 表示第i个位置对于前j个数的答案
那么答案区间\(l,r\)要求的无非就是\(\sum_{i=l}^r f(i,i)-f(i,l-1)\)
像\(f(i,i)\)这种可以预处理出来，要求的就只剩后一部分
如果已知\(L,R\)的答案考虑如何转移到\(l,r\)
case 1 L<l
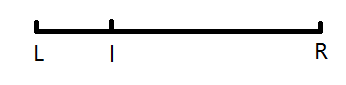
case 2 l<L
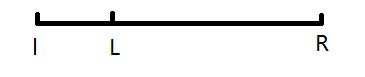
case 3 r<R
case 4 R<r
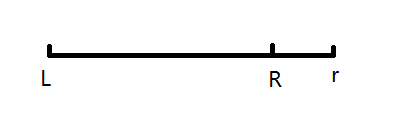
把这些修改离线下来
