*[题解]GFUOJ2311~2313（提高十连测day3）

2311 简单的玄学

反面考虑。选第一个数的概率是\({2^n}\over{2^n}\),第二个的是\({2^n-1}\over{2^n}\)，第三个的是\({2^n-2}\over{2^n}\)，以此类推

则总概率为\({A_{2^n}^m}\over{2^{nm}}\)=\({2^{n(m-1)}-\prod_{1=2^n-m+1}^{2^n-1}}\over{2^{n(m-1)}}\)

分母用快速幂。分子看上去不好求，但是\(m \ge 10^6+3\)，乘积中必有\(mod\)的倍数，结果一定是0。暴力即可

考虑约分。

未完待续

2312 旅行

因为每条边可以通过的区间是连续的，所以答案的区间也是

并且答案区间的端点从这些边的中产生

很明显，可以想到“带哪些会走不到”（即不连通）

于是产生了一个暴力做法：枚举选的区间的左端点，二分右端点

每次进行一个并查集

时间：\(O(m^2log_m)\)

然而，我们发现加边是一个动态过程，右端点往左枚相当于顺序加边

于是就有了一个\(O(m^2)\)的做法（正解）

代码：

#include<bits/stdc++.h>
#define N 110000
using namespace std;
int n,m,tot,ans,pos,head[N],fa[N],r[N];
struct nd{
	int x,y,l,r;
}a[5*N];
bool cmp(nd a,nd b){
	return a.l>b.l;
}
int getf(int x){
	if(fa[x]==x)return x;
	return fa[x]=getf(fa[x]);
}
void merge(int x,int y){
	x=getf(x),y=getf(y);
	fa[x]=y;
}
bool pd(int x,int y){
	if(getf(x)==getf(y))return 1;
	return 0;
}
void solve(int k){
	for(int i=1;i<=n;i++)fa[i]=i;
//	for(int i=1;i<=m;i++){
	for(int i=m;i>0;i--){
		if(a[i].r>=r[k]){
			merge(a[i].x,a[i].y);
			if(pd(1,n)&&r[k]-a[i].l+1>ans){
				ans=r[k]-a[i].l+1;
				pos=a[i].l;
			}
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)scanf("%d%d%d%d",&a[i].x,&a[i].y,&a[i].l,&a[i].r),r[i]=a[i].r;
	sort(r+1,r+m+1);
	sort(a+1,a+m+1,cmp);
	for(int i=1;i<=m;i++)solve(i);
	printf("%d\n",ans);
	for(int i=pos;i<=pos+ans-1;i++)printf("%d ",i);
}

2313 词典

首先，拿\(T_i\)建一颗Trie

建出来如下图

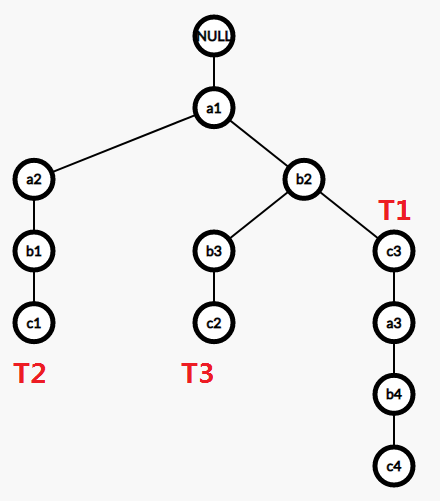
再看询问

S1找到了点“a2”，所在最长字符串为T2

经过找规律发现答案就是n-i

而S2所对的点不在任何字符串内，即在0号字符串内，答案为3

代码：

#include<bits/stdc++.h>
#define N 3300000
using namespace std;
int n,m,cnt=1,mx[N],nw[N],id[N],t[N][7];
char s[N];
void updata(int u,int id){
	int l=strlen(s);
	for(int i=0;i<l;i++){
		if(t[u][s[i]-'a']==0)t[u][s[i]-'a']=++cnt;
		u=t[u][s[i]-'a'];
		mx[u]=max(mx[u],id-nw[u]-1);
		nw[u]=id;
	}
}
int query(int u){
	int l=strlen(s);
	for(int i=0;i<l;i++){
		if(t[u][s[i]-'a']==0)return n;
		u=t[u][s[i]-'a'];
	}
	return max(mx[u],n-nw[u]);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%s",s);
		updata(1,i);
	}
	for(int i=1;i<=m;i++){
		scanf("%s",s);
		printf("%d\n",query(1));
	}
}