树

树

树

概念

　　树是一种数据结构。比如：目录结构。

　　树是一种可以递归定义的数据结构。

　　树是有n个节点组成的集合。

　　　　如果n=0，那这是一棵空树；

　　　　如果n>0，那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树。

 

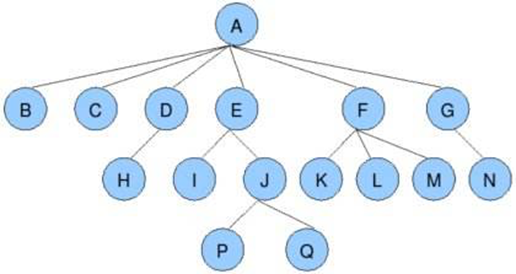
根节点

 　　如上图所示，A节点为根节点。

叶子节点

 　　所有没有孩子的节点都为叶子节点。如B节点、C节点、H节点、I节点、P节点、Q节点、K节点、L节点、M节点、N节点。

树的深度（高度）

 　　树有几层，深度就位多少。如上图所示，其深度为4。

树的度

 　　节点的度就是其有几个孩子，例如E节点的度为2，F节点的度为3。

　　树的度就是其最大的节点的度。例如上图所示的树的度为6。树的度不一定就是根节点，看的是最大。

孩子节点/父节点

 　　如上图所示，A叫做C的父节点。C叫做A的孩子节点。

子树

 　　树的一部分就是一棵子树。树的任何一个节点都是一个子树，不管其有没有子节点，但是其必须是完整的。

 二叉树

概念

　　二叉树是度不超过2的树（节点最多有两个叉）。如图所示：

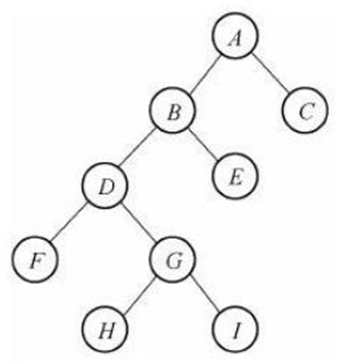
　　其中B叫做A的左孩子，C叫做A的右孩子。其顺序是固定的。

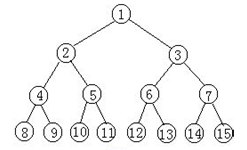
满二叉树

　　一个二叉树，如果每一层的节点数都达到了最大的值，则这个二叉树就是满二叉树。如下图所示：

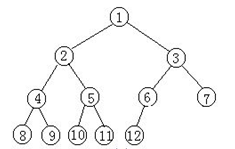
完全二叉树

 　　叶节点只能出现在最下层和次下层，并且最下面一层的节点都集中在在该层最左边的若干位置的二叉树。如下图所示：

 

二叉树的存储方式

链式存储方式

顺序存储方式（列表）

　　顺序存储方式使用的列表存储，但是其只能存储完全二叉树。如图所示：

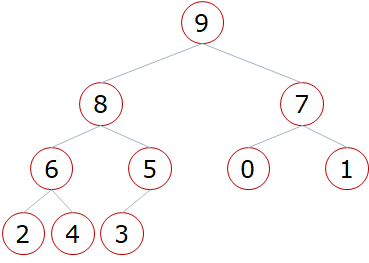
其存储顺序为：9-8-7-6-5-0-1-2-4-3

　　如果一个父节点的下标（存储列表的索引）为i，则其左孩子的下标为2i+1。

　　如果一个父节点的下标（存储列表的索引）为i，则其右孩子的下标为2i+2。

 　　如果孩子的下标为i，则其父节点的下标为(i-1)//2。