WC2011 最大路径异或和
WC2011 最大XOR和路径
1 题目
-
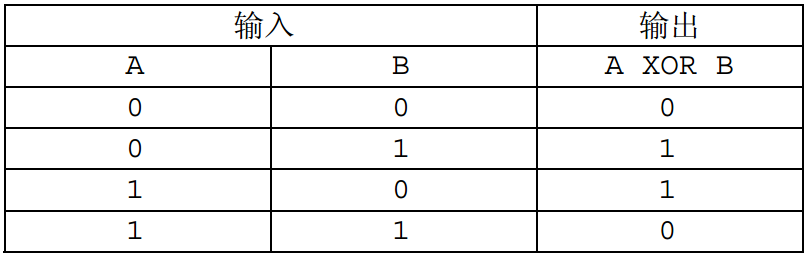
XOR(异或)是一种二元逻辑运算,其运算结果当且仅当两个输入的布尔值不相等时才为真,否则为假。 XOR 运算的真值表如下(1 表示真, 0表示假):
而两个非负整数的 XOR 是指将它们表示成二进制数,再在对应的二进制位进行 XOR 运算。
譬如 12 XOR 9 的计算过程如下:
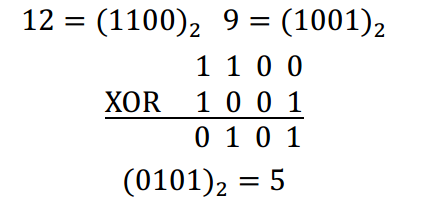
故 12 XOR 9 = 5。
容易验证, XOR 运算满足交换律与结合律,故计算若干个数的 XOR 时,不同的计算顺序不会对运算结果造成影响。从而,可以定义 K个非负整数 \(A_1,A_2,……,A_{K-1},A_K\)的 XOR 和为
\(A_1 XOR A_2 XOR …… XOR A_{K-1} XOR A_K\)
考虑一个边权为非负整数的无向连通图,节点编号为 1到 N,试求出一条从 11 号节点到 NN 号节点的路径,使得路径上经过的边的权值的 XOR 和最大。
路径可以重复经过某些点或边,当一条边在路径中出现了多次时,其权值在计算 XOR 和时也要被计算相应多的次数,具体见样例。
2 分析
-
本题的关键就是对环的处理。题目告诉我们路径和点是可以重复经过的。 根据异或的性质,一条路来回走等于没有走。
-
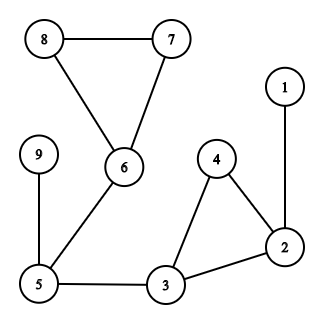
我们发现从1到n的路径上会存在两种环。 如下图所示,n=9。
-
假设我们从\(1 \rightarrow 2 \rightarrow 3 \rightarrow 5 \rightarrow9\)。 中间我们经过两种环,一个是包含了路径的环,即[2,3,4],还有是和路径无关的环[6,7,8]。为什么[6,7,8]和路径无关呢,因为我们可以把这个环看成是在路径之外额外添加的。边(5,6)由于走了两次,所以相当于不存在。 我们可以通过灌水把和起点1连通的所有环的异或和全部都算出来。
-
然后我们随便选择一条从起点到终点的路径,假如说就是\(1 \rightarrow 2 \rightarrow 3 \rightarrow 5 \rightarrow 9\),那么我们外加环[6,7,8]就可以得到我们的最优值。有些同学可以会问,如果我们一开始选择的是\(1 \rightarrow 2 \rightarrow 4 \rightarrow 3 \rightarrow 3 \rightarrow 5 \rightarrow 9\),如果这条路路径比原路径更好,那么我们是不是答案就错掉了。其实没关系,因为我们即使选择了\(1 \rightarrow 2 \rightarrow 3 \rightarrow 5 \rightarrow 9\),我们也可以异或环[2,3,4],这就把[2,3]这条边给消去了,添加了[2,4]和[4,3]这两条边。
-
所以总的思路已经很明显了,我们只要先随便找一条从起点到终点的路,然后用这里的环去异或这个路径。 那么如何才能求得异或的最大值呢?我们可以对所有环求线性基,然后假设当前路径的异或值是V,那么我们从大到小枚举线性基,如果ans异或了当前的d[i]以后可以变大,就异或一下,否则就不要异或。 这个贪心其实很好理解,如果ans是\((010010)_2\),当前的d[i]的最高位如果比ans大,那么我们肯定要异或进去。如果当前的i是4,那么此时ans异或d[4]肯定变小,而且以后再怎么补也补不回来。同理,i比4小的时候也是如此。
-
总的时间复杂度:\(O(n+m+60\times n)\),前面是灌水的时间复杂度,后面是建立线性基的最坏时间复杂度。
3 代码
#include<bits/stdc++.h>
using namespace std;
#define N 50005
#define M 100005
#define ll long long
struct edge{
int to,nt;
ll w;
}e[M<<1];
int h[N],cnt,n,m,vis[N];
ll t[N],d[70];
void add(int a,int b,ll c){
e[++cnt].to=b; e[cnt].w=c; e[cnt].nt=h[a]; h[a]=cnt;
}
void ins(ll x){
for(int i=62;i>=0;i--)
if(x&(1LL<<i)){
if(d[i]) x^=d[i];
else {
d[i]=x;
break;
}
}
}
void dfs(int x,ll val){
t[x]=val;
vis[x]=1;
for(int i=h[x];i;i=e[i].nt){
int v=e[i].to;
if(!vis[v]) dfs(v,val^e[i].w);
else ins(val^e[i].w^t[v]);
}
}
int main(){
scanf("%d%d",&n,&m);
while (m--){
int x,y;
ll z;
scanf("%d%d%lld",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
dfs(1,0);
ll ans=t[n];
for(int i=62;i>=0;i--)
ans=max(ans,ans^d[i]);
printf("%lld\n",ans);
return 0;
}



