cf1301e

cf1301e Nanosoft

1.题目大意

​ 给你一个\(n*m\)的矩形，里面有四种颜色的格子，\(Y\)表示黄色，\(B\)表示蓝色，\(G\)表示绿色，\(R\)表示红色，要求你找出左上角全部都是红色，右上角全部都是绿色，左下角全部都是黄色，右下角全部都是蓝色的最大子矩形。有\(Q\)个询问，每个询问给你\(r1,c1,r2,c2\)表示你要这个子矩形里面找到最大的满足条件的子矩形。

​ 合法的矩形如下图所示：

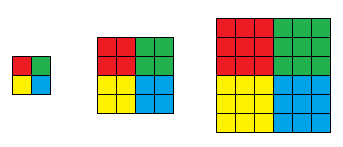
2.数据范围

​ \(1 \leq n,m \leq 500,1 \leq Q \leq 3*10^5\)

3.思路

​ 我们可以从二分的角度考虑这个问题，我们先计算出以下面这个\(X\)为中心点的最大满足条件的子矩阵。

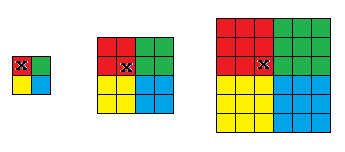
​ 求这个的满足条件的最大子矩阵可以用二分和维护矩形前缀和来实现。时间复杂度: \(O(n*m*logn)\)，算出来的值用\(val\)数组表示。

​ 如这个图所示：

​ 我们就可以得到的\(val\)数组如下：

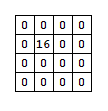
​ 然后我们维护一个二维的st表，对于每个询问\(r1,c1,r2,c2\)，我们只要看在矩形\((r1+mid-1,c1+mid-1,r2-mid,c2-mid)\)这个矩形里面是有最大值超过等于\(mid\)。 建立st表的时间复杂度是\(O(n*m*logn*logm)\)。处理询问的总的时间复杂度\(O(q*logn)\)。

​ 所以总的时间复杂度： \(O(n*m*logn*logm+q*logn)\)

​ 附录代码：

#include<bits/stdc++.h>  
using namespace std;  
int const N=500+10; 
char s[N][N];  
int  a[N][N],st[N][N][10][10],n,m,q,num[N][N][4],rk[200],lg[2000];  
int calc(int x1,int y1,int x2,int y2,int c){
    int t=num[x2][y2][c]-num[x1-1][y2][c]-num[x2][y1-1][c]+num[x1-1][y1-1][c];  
    return t; 
}
int check(int mid,int x,int y){
    if(x-mid+1<1 || y-mid+1<1 || x+mid>n || y+mid>m)  
        return 0; 
    int t=mid*mid;  
    return calc(x-mid+1,y-mid+1,x,y,2 )==t && calc(x-mid+1,y+1,x,y+mid,0)==t &&  
    calc(x+1,y-mid+1,x+mid,y,1)==t && calc(x+1,y+1,x+mid,y+mid,3)==t;  
}
void build_st(){
    for(int i=1;i<=10;i++)  
        for(int j=(1<<i-1);j<(1<<i);j++)  
            lg[j]=i-1;  
    for(int i=1;i<=n;i++) 
        for(int j=1;j<=m;j++)  
            st[i][j][0][0]=a[i][j];  
    for(int x=0;x<10;x++)   
        for(int y=0;y<10;y++)  
            for(int i=1;i<=n;i++)  
                for(int j=1;j<=m;j++) {
                    if(x==0 && y==0) continue;  
                    if(x==0 && y) { 
                        if(j+(1<<y-1)<=m) 
                            st[i][j][x][y]=max(st[i][j][x][y-1],st[i][j+(1<<y-1)][x][y-1]);  
                        else 
                            st[i][j][x][y]=st[i][j][x][y-1];  
                        continue;  
                    }
                    if(i+(1<<x-1)<=n) 
                        st[i][j][x][y]=max(st[i][j][x-1][y],st[i+(1<<x-1)][j][x-1][y]); 
                    else 
                        st[i][j][x][y]=st[i][j][x-1][y];  
                }
}
int test(int mid,int x1,int y1,int x2,int y2){
    int r1=x1+mid-1;  
    int c1=y1+mid-1;  
    int r2=x2-mid;  
    int c2=y2-mid;  
    if(r1>r2 || c1>c2 ) return 0;  
    int k1=lg[r2-r1+1];  
    int k2=lg[c2-c1+1];  
    return max(max(st[r1][c1][k1][k2],st[r1][c2-(1<<k2)+1][k1][k2]),
    max(st[r2-(1<<k1)+1][c1][k1][k2],st[r2-(1<<k1)+1][c2-(1<<k2)+1][k1][k2]))>=4*mid*mid; 
}
int main(){
    scanf("%d%d%d",&n,&m,&q);  
    rk['G']=0;  
    rk['Y']=1;  
    rk['R']=2;  
    rk['B']=3;  
    for(int i=0;i<n;i++) 
        scanf("%s",s[i]); 
    for(int i=1;i<=n;i++)  
        for(int j=1;j<=m;j++) {
            for(int k=0;k<4;k++)  
                num[i][j][k]=num[i-1][j][k]+num[i][j-1][k]-num[i-1][j-1][k];  
            int x=rk[s[i-1][j-1]];  
            num[i][j][x]++;    
        }
    for(int i=1;i<=n;i++)  
        for(int j=1;j<=m;j++) {
            int l=0,r=250;  
            while (l<r){
                int mid=(l+r+1)/2;  
                if(check(mid,i,j)) 
                    l=mid;  
                else 
                    r=mid-1; 
            }
            a[i][j]=4*l*l; 
        }
    build_st();  
    while (q--){
        int x1,x2,y1,y2;  
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);  
        int l=0,r=250;  
        while (l<r){
            int mid=(l+r+1)/2;  
            if(test(mid,x1,y1,x2,y2))
                l=mid;  
            else 
                r=mid-1;  
        }
        printf("%d\n",4*l*l);  
    }
    return 0; 
}